Trong các số từ 40 đến 253, có bao nhiêu số chia hết cho ít nhất một trong hai số 10 và 11.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số lớn nhất trong khoảng đã cho chia hết cho 5 là: 130
Số lớn nhất trong khoảng đã cho chia hết cho 7 là: 133
Số chia hết cho 5 trong khoảng đã cho:
\(130:5=26\left(số\right)\)
Số chia hết cho 7 trong khoảng đã cho:
\(133:7=19\left(số\right)\)
Trong khoảng đã cho có số lượng các số ít nhất chia hết cho 5 và 7 là:
\(26+19=45\left(số\right)\)
Đáp số: \(45số\)
Các số chia hết cho 5 là \(5;10;15;...;130\)
Số các số chia hết cho 5 là
\(\left(130-5\right)\div5+1=26\) (số)
Các số chia hết cho 7 là \(7;14;21;...;133\)
Số các số chia hết cho 7 là
\(\left(133-7\right)\div7+1=19\) (số)
Các số chia hết cho 5 và 7
=> Các số chia hết cho 35
Các số chia hết cho 35 là \(35;70;105\)
Số các số chia hết 5 và 7 là 3 (số)
Số các số chia hết cho ít nhất một trong hai số 5 và 7 là
\(26+19-3=42\) (số)


A = \(\dfrac{n^9+1}{n^{10}+1}\)
\(\dfrac{1}{A}\) = \(\dfrac{n^{10}+1}{n^9+1}\) = n - \(\dfrac{n-1}{n^9+1}\)
B = \(\dfrac{n^8+1}{n^9+1}\)
\(\dfrac{1}{B}\) = \(\dfrac{n^9+1}{n^8+1}\) = n - \(\dfrac{n-1}{n^8+1}\)
Vì n > 1 ⇒ n - 1> 0
\(\dfrac{n-1}{n^9+1}\) < \(\dfrac{n-1}{n^8+1}\)
⇒ n - \(\dfrac{n-1}{n^9+1}\) > n - \(\dfrac{n-1}{n^8+1}\)⇒ \(\dfrac{1}{A}>\dfrac{1}{B}\)
⇒ A < B

\(1\dfrac{7}{20}\div2,7+2,7\div1,35+\left(0,4\div2\dfrac{1}{2}\right)\times\left(4,2-1\dfrac{3}{40}\right)\)
\(=\dfrac{27}{20}\div\dfrac{27}{10}+\dfrac{27}{10}\div\dfrac{27}{20}+\left(\dfrac{2}{5}\div\dfrac{5}{2}\right)\times\left(\dfrac{21}{5}-\dfrac{43}{40}\right)\)
\(=\dfrac{27}{20}\times\dfrac{10}{27}+\dfrac{27}{10}\times\dfrac{20}{27}+\left(\dfrac{2}{5}\times\dfrac{2}{5}\right)\times\dfrac{25}{8}\)
\(=\dfrac{1}{2}+2+\dfrac{4}{25}\times\dfrac{25}{8}\)
\(=\dfrac{5}{2}+\dfrac{1}{2}\)
\(=3\)

M = {\(x\)|\(x\) là số tự nhiên lẻ, 26 < \(x\) ≤ 44}
Các số tự nhiên lẻ lớn hơn 26 và không vượt quá 44 là các số thuộc dãy số sau:
27; 29;...;43
Dãy số trên là dãy số cách đều với khoảng cách là: 29 - 27 = 2
Dãy số trên có số số hạng là: (43 - 27): 2 + 1 = 9 (số)
Vậy tập M có 9 phần tử
N = {\(x\in\)N|\(x\) chia hết cho 5; \(x\) < 16}
N = { 0; 5; 10; 15}
Tập N có 4 phần tử
Tổng số phần tử của tập M và tập N là:
9 + 4 = 13
Chọn C.13


a)
\(\left(14^{19}-14^{18}\right)\div\left(14^5\times14^{12}\right)\)
\(=\left(14^{19}-14^{18}\right)\div14^{17}\)
\(=\left(14^{19}-14^{18}\right)\times\dfrac{1}{14^{17}}\)
\(=\dfrac{14^{19}-14^{18}}{14^{17}}=\dfrac{14^{18}\times\left(14-1\right)}{14^{17}}\)
\(=14\times13=182\)
b)
\(\left(2^{41}+3^8\right)\times\left(10^7-2^7\right)\times\left(2^4-4^2\right)\)
\(=\left(2^{41}+3^8\right)\times\left(10^7-2^7\right)\times\left(2^4-2^4\right)\)
\(=\left(2^{41}+3^8\right)\times\left(10^7-2^7\right)\times0\)
\(=0\)

Vì ABCD là hình chữ nhật nên: AB = DC = 16 cm
EF vuông góc DC ⇒ BCFE là hình chữ nhật ⇒ EF = BC = 13 cm
Diện tích tam giác DEC là:
16 \(\times\) 13: 2 = 104 (cm2)
Đáp số: 104 cm2
 CÍU VỚI< GẤP
CÍU VỚI< GẤP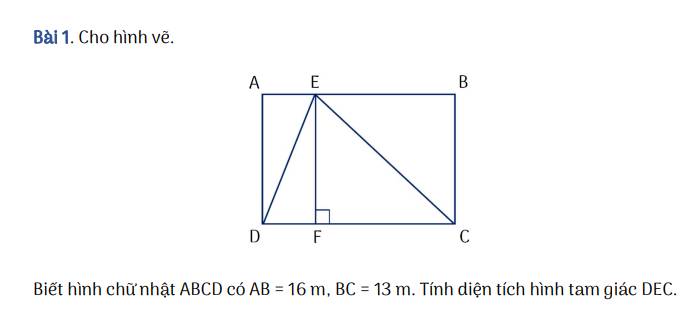
Trong khoảng đã cho:
Số nhỏ nhất chia hết cho 10 là 40.
Số lớn nhất chia hết cho 10 là 250.
Số nhỏ nhất chia hết cho 11 là 44.
Số lớn nhất chia hết cho 11 là 253.
Số các số chia hết cho 10:
\(\dfrac{250-40}{10}+1=22\left(số\right)\)
Số các số chia hết cho 11:
\(\dfrac{253-44}{11}+1=20\left(số\right)\)
Có 2 số chia hết cho 10 và 11 là 110 và 220.
Số lượng số ít nhất chia hết cho 10 và 11 là:
\(22+20-2=40\left(số\right)\)
Đáp số: 40 số