Tìm x để \(\frac{\sqrt{x}-4}{\sqrt{x}-2}< 1\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1)
\(y=x-\sqrt{x-1991}=\left(\sqrt{x-1991}-\frac{1}{2}\right)^2+\frac{7963}{4}\ge\frac{7963}{4}\)
Dấu "=" xảy ra khi \(x=\frac{7965}{4}\)
2)
\(T=\frac{2a^2+4ab+5b^2}{a^2+b^2}=\frac{\left(a+2b\right)^2}{a^2+b^2}+1\ge1\)
Dấu "=" xảy ra khi a=-2b
\(T=\frac{2a^2+4ab+5b^2}{a^2+b^2}=-\frac{\left(2a-b\right)^2}{a^2+b^2}+6\le6\)
Dấu "=" xảy ra khi 2a=b

Với a>0,a≠4 và a≠1, ta có:
Q=(1√a−1−1√a):(√a+1√a−2−√a+2√a−1)
=√a−(√a−1)√a(√a−1):(√a+1)(√a−1)−(√a+2)(√a−2)(√a−2)(√a−1)
=√a−√a+1√a(√a−1):a−1−(a−4)(√a−2)(√a−1)
=1√a(√a−1):3(√a−2)(√a−1)
=1√a(√a−1).(√a−2)(√a−1)3
=√a−23√a
Với \(a>0\), \(a\ne4\)và \(a\ne1\)ta có:
\(Q=\left(\frac{1}{\sqrt{a}-1}-\frac{1}{\sqrt{a}}\right):\left(\frac{\sqrt{a}+1}{\sqrt{a}-2}-\frac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\left[\frac{\sqrt{a}}{\sqrt{a}.\left(\sqrt{a}-1\right)}-\frac{\sqrt{a}-1}{\sqrt{a}.\left(\sqrt{a}-1\right)}\right]:\left[\frac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\frac{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right]\)
\(=\frac{\sqrt{a}-\left(\sqrt{a}-1\right)}{\sqrt{a}.\left(\sqrt{a}-1\right)}:\left[\frac{a-1}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\frac{a-4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right]\)
\(=\frac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}.\left(\sqrt{a}-1\right)}:\frac{\left(a-1\right)-\left(a-4\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\frac{1}{\sqrt{a}.\left(\sqrt{a}-1\right)}:\frac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\frac{1}{\sqrt{a}.\left(\sqrt{a}-1\right)}:\frac{3}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\frac{1}{\sqrt{a}.\left(\sqrt{a}-1\right)}.\frac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)
\(=\frac{\sqrt{a}-2}{3\sqrt{a}}\)

từ giả thiết \(\Rightarrow3xy=x+y+1\)
áp dụng bất đẳng thức Bunia ta có
\(3x^2+1\ge\frac{\left(3x+1\right)^2}{4}\Rightarrow\sqrt{3x^2+1}\ge\frac{\left(3x+1\right)}{2}\)
tương tự \(\Rightarrow\frac{1}{\sqrt{3x^2+1}}+\frac{1}{\sqrt{3y^2+1}}\le\frac{2}{3x+1}+\frac{2}{3y+1}\)
Mà \(\frac{2}{3x+1}+\frac{2}{3y+1}=\frac{6x+6y+4}{9xy+3x+3y+1}=\frac{6x+6y+4}{6x+6y+4}=1\)(Thế \(3xy=x+y+1\))
từ đây ta có dpcm
Ta có: \(\left(x+1\right)\left(y+1\right)=4xy\Rightarrow xy+x+y+1=4xy\Rightarrow3xy=x+y+1\)
Xét bất đẳng thức phụ \(3x^2+1\ge\frac{\left(3x+1\right)^2}{4}\)(*)
Thật vậy: (*)\(\Leftrightarrow12x^2+4-9x^2-6x-1\ge0\Leftrightarrow3x^2-6x+3\ge0\Leftrightarrow3\left(x-1\right)^2\ge0\)*đúng*
Do đó \(\sqrt{3x^2+1}\ge\frac{3x+1}{2}\Rightarrow\frac{1}{\sqrt{3x^2+1}}\le\frac{2}{3x+1}\)(1)
Tương tự, ta có: \(\frac{1}{\sqrt{3y^2+1}}\le\frac{2}{3y+1}\)(2)
Cộng theo vế hai bất đẳng thức (1) và (2), ta được: \(\frac{1}{\sqrt{3x^2+1}}+\frac{1}{\sqrt{3y^2+1}}\le\frac{2}{3x+1}+\frac{2}{3y+1}=\frac{6x+6y+4}{9xy+3x+3y+1}=\frac{6x+6y+4}{3\left(x+y+1\right)+3x+3y+1}=\frac{6x+6y+4}{6x+6y+4}=1\)Đẳng thức xảy ra khi x = y = 1

từ phương trình 1 ta có \(x^2+y^2=4\)(*) thế xuống phương trình 2 ta được
\(2x^2=\left(x+y\right).\left(x^2+y^2-xy\right)=x^3+y^3\) hay \(x^2\left(2-x\right)=y^3\)(**)
Từ (*) ta có \(\hept{\begin{cases}x,y\le2\\y=\pm\sqrt{4-x^2}\end{cases}}\), mà vế trái của (**) là số dương, do đó y là số dương hay \(y=\sqrt{4-x^2}\)thế vào (**) được
\(x^2\left(2-x\right)=\sqrt{\left(4-x^2\right)^3}=\sqrt{\left(2-x\right)^3.\left(2+x\right)^3}\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x^2=\sqrt{\left(2-x\right)\left(2+x\right)^3}\end{cases}}\)với x=2 thì y=0
với \(x^2=\sqrt{\left(2-x\right)\left(2+x\right)^3}\Leftrightarrow x^4=16-x^4+16x-4x^3\)
\(\Leftrightarrow x^4+2x^3-8x-8=0\)\(\Leftrightarrow\orbr{\begin{cases}x=1.806816\Rightarrow y=0.85756\\x=-1.165044\Rightarrow y=1.625629\end{cases}}\) thỏa mãn hệ
Vậy hệ có ba nghiệm như trên


Xin phép được sửa đề : \(\sqrt{2059-x}+\sqrt{2035-x}+\sqrt{2154-x}=24\)( ĐKXĐ : \(x\le2035\))
\(\Leftrightarrow\sqrt{2059-x}-7+\sqrt{2035-x}-5+\sqrt{2154-x}-12=24-7-5-12\)
\(\Leftrightarrow\left[\left(\sqrt{2059-x}\right)^2-7^2\right]\frac{1}{\sqrt{2059-x}+7}\)\(+\left[\left(\sqrt{2035-x}\right)^2-5^2\right]\frac{1}{\sqrt{2035-x}+5}\)\(+\left[\left(\sqrt{2154-x}\right)^2-12^2\right]\frac{1}{\sqrt{2154-x}+12}=0\)
\(\Leftrightarrow\left(2059-x-49\right)\frac{1}{\sqrt{2059-x}+7}+\left(2035-x-25\right)\frac{1}{\sqrt{2035-x}+5}+\left(2154-x-144\right)\frac{1}{\sqrt{2154-x}+12}=0\)
\(\Leftrightarrow\left(2010-x\right)\frac{1}{\sqrt{2059-x}+7}+\left(2010-x\right)\frac{1}{\sqrt{2035-x}+5}+\left(2010-x\right)\frac{1}{\sqrt{2154-x}+12}=0\)
\(\Leftrightarrow\left(2010-x\right)\left(\frac{1}{\sqrt{2059-x}+7}+\frac{1}{\sqrt{2035-x}+5}+\frac{1}{\sqrt{2154-x}+12}\right)=0\)
Mà \(\frac{1}{\sqrt{2059-x}+7}+\frac{1}{\sqrt{2035-x}+5}+\frac{1}{\sqrt{2154-x}+12}>0\)
\(\Leftrightarrow2010-x=0\Leftrightarrow x=2010\)( TMĐK )
Vậy...

Có ĐKXĐ : \(x-\frac{1}{x}\ge0;x\ne0\)
\(\Leftrightarrow x+2\sqrt{x-\frac{1}{x}}=4+\frac{1}{x}\)( chia 2 vế cho x )
\(\Leftrightarrow x-\frac{1}{x}+2\sqrt{x-\frac{1}{x}}-4=0\)
Đặt : \(t=\sqrt{x-\frac{1}{x}}\Rightarrow\)ta có pt : \(t^2+2t-4=0\)
\(\Leftrightarrow t^2+2t+1-5=0\)
\(\Leftrightarrow\left(t+1\right)^2=5\)
\(\Leftrightarrow t+1=\sqrt{5}\Leftrightarrow t=\sqrt{5}-1\)
\(\Rightarrow\sqrt{x-\frac{1}{x}}=\sqrt{5}-1\)
\(\Leftrightarrow\frac{x^2-1}{x}=6-2\sqrt{5}\)
\(\Leftrightarrow x^2-1-6x+2x\sqrt{5}=0\)
Không biết mình sai ở đâu nma đến đây thì mình chịu gòy :'
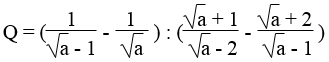
\(ĐKXĐ:\hept{\begin{cases}x\ge0\\x\ne4\end{cases}}\)
\(\frac{\sqrt{x}-4}{\sqrt{x}-2}=\frac{\sqrt{x}-2-2}{\sqrt{x}-2}=\frac{\sqrt{x}-2}{\sqrt{x}-2}-\frac{2}{\sqrt{x}-2}=1-\frac{2}{\sqrt{x}-2}\)
Để \(\frac{\sqrt{x}-4}{\sqrt{x}-2}< 1\)thì \(1-\frac{2}{\sqrt{x}-2}< 1\)
\(\Rightarrow\frac{2}{\sqrt{x}-2}>0\)\(\Rightarrow\sqrt{x}-2>0\)( vì \(2>0\))
\(\Leftrightarrow\sqrt{x}>2\)\(\Leftrightarrow x>4\)( thỏa mãn ĐKXĐ )
Vậy với \(x>4\)thì \(\frac{\sqrt{x}-4}{\sqrt{x}-2}< 1\)