x+1/10+x+1/10=x+1/21
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(27^5:9^6\)
\(=\left(3^3\right)^5:\left(3^2\right)^6\)
\(=3^{15}:3^{12}\)
\(=3^{15-12}\)
\(=3^3\)

\(\left(7\dfrac{4}{9}+4\dfrac{7}{11}\right)-3\dfrac{4}{9}\)
\(=\dfrac{67}{9}+\dfrac{51}{11}-\dfrac{31}{9}\)
\(=\dfrac{67}{9}-\dfrac{31}{9}+\dfrac{51}{11}\)
\(=4+\dfrac{51}{11}\)
\(=\dfrac{95}{11}\)
Chúc bạn học tốt

`@` `\text {Ans}`
`\downarrow`
\(\left(x-\dfrac{1}{3}\right)^2=x-\dfrac{1}{3}\)
`\Rightarrow`\(\left(x-\dfrac{1}{3}\right)^2-\left(x-\dfrac{1}{3}\right)^1=0\)
`\Rightarrow`\(\left(x-\dfrac{1}{3}\right)\left(x-\dfrac{1}{3}-1\right)=0\)
`\Rightarrow`\(\left[{}\begin{matrix}x-\dfrac{1}{3}=0\\x-\dfrac{4}{3}=0\end{matrix}\right.\)
`\Rightarrow`\(\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)
Vậy, `x \in`\(\left\{\dfrac{1}{3};\dfrac{4}{3}\right\}.\)

`@` `\text {Ans}`
`\downarrow`
`a)`
\(5^x+5^{x+2}=650\)
`\Rightarrow 5^x + 5^x . 5^2 = 650`
`\Rightarrow 5^x . (1 + 5^2) = 650`
`\Rightarrow 5^x . 26 = 650`
`\Rightarrow 5^x = 650 \div 26`
`\Rightarrow 5^x = 25`
`\Rightarrow 5^x = 5^2`
`\Rightarrow x = 2`
Vậy, `x = 2`
`b)`
`(4x + 1)^2 = 25.9`
`\Rightarrow (4x + 1)^2 = 225`
`\Rightarrow (4x + 1)^2 = (+-15^2)`
`\Rightarrow`\(\left[{}\begin{matrix}4x-1=15\\4x-1=-15\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}4x=16\\4x=-14\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}x=4\\x=-\dfrac{7}{2}\end{matrix}\right.\)
Vậy, `x \in`\(\left\{-\dfrac{7}{2};4\right\}\)
`c)`
\(2^x+2^{x+3}=144\)
`\Rightarrow 2^x + 2^x . 2^3 = 144`
`\Rightarrow 2^x . (1 + 2^3) = 144`
`\Rightarrow 2^x . 9 = 144`
`\Rightarrow 2^x = 144 \div 9`
`\Rightarrow 2^x = 16`
`\Rightarrow 2^x = 2^4`
`\Rightarrow x = 4`
Vậy, `x = 4`
`d)`
\(3^{2x+2}=9^{x+3}\)
`\Rightarrow `\(3^{2x+2}=\left(3^2\right)^{x+3}\)
`\Rightarrow `\(3^{2x+2}=3^{2x+6}\)
`\Rightarrow 2x + 2 = 2x + 6`
`\Rightarrow 2x - 2x = 6 - 2`
`\Rightarrow 0 = 4 (\text {vô lý})`
Vậy, `x` không có giá trị nào thỏa mãn.
`e)`
\(x^{15}=x^2\)
`\Rightarrow `\(x^{15}-x^2=0\)
`\Rightarrow `\(x^2\cdot\left(x^{13}-1\right)=0\)
`\Rightarrow `\(\left[{}\begin{matrix}x^2=0\\x^{13}-1=0\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}x=0\\x^{13}=1\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy, `x \in`\(\left\{0;1\right\}.\)

`@` `\text {Ans}`
`\downarrow`
`a)`
\(\dfrac{7}{5}\cdot\dfrac{8}{19}+\dfrac{7}{5}\cdot\dfrac{12}{19}-\dfrac{7}{5}\cdot\dfrac{1}{19}\)
`=`\(\dfrac{7}{5}\cdot\left(\dfrac{8}{19}+\dfrac{12}{19}-\dfrac{1}{19}\right)\)
`=`\(\dfrac{7}{5}\cdot\dfrac{19}{19}=\dfrac{7}{5}\cdot1=\dfrac{7}{5}\)
`b)`
\(-\dfrac{3}{5}\cdot\dfrac{5}{7}+\left(-\dfrac{3}{5}\right)\cdot\dfrac{3}{7}+\left(-\dfrac{3}{5}\right)\cdot\dfrac{6}{7}\)
`=`\(-\dfrac{3}{5}\cdot\left(\dfrac{5}{7}+\dfrac{3}{7}+\dfrac{6}{7}\right)\)
`=`\(-\dfrac{3}{5}\cdot\dfrac{14}{7}\)
`=`\(-\dfrac{3}{5}\cdot2=-\dfrac{6}{5}\)
`c)`
\(10\dfrac{2}{9}+\left(2\dfrac{2}{5}-7\dfrac{2}{9}\right)\)
`=`\(10\dfrac{2}{9}+2\dfrac{2}{5}-7\dfrac{2}{9}\)
`=`\(\left(10\dfrac{2}{9}-7\dfrac{2}{9}\right)+2\dfrac{2}{5}\)
`=`\(3+2\dfrac{2}{5}=\dfrac{27}{5}\)
`d)`
\(6\dfrac{3}{10}-\left(3\dfrac{4}{7}+2\dfrac{3}{10}\right)\)
`=`\(6\dfrac{3}{10}-3\dfrac{4}{7}-2\dfrac{3}{10}\)
`=`\(\left(6\dfrac{3}{10}-2\dfrac{3}{10}\right)-3\dfrac{4}{7}\)
`=`\(4-3\dfrac{4}{7}=\dfrac{3}{7}\)
a) \(\dfrac{7}{5}.\dfrac{8}{19}+\dfrac{7}{5}.\dfrac{12}{19}-\dfrac{7}{5}.\dfrac{1}{19}\)
\(=\dfrac{7}{5}.\left(\dfrac{8}{19}+\dfrac{12}{19}-\dfrac{1}{19}\right)\)
\(=\dfrac{7}{5}.1\)
\(=\dfrac{7}{5}\)
b) \(\dfrac{-3}{5}.\dfrac{5}{7}+\dfrac{-3}{5}.\dfrac{3}{7}+\dfrac{-3}{5}.\dfrac{6}{7}\)
\(=\dfrac{-3}{5}.\left(\dfrac{5}{7}+\dfrac{3}{7}+\dfrac{6}{7}\right)\)
\(=\dfrac{-3}{5}.2\)
\(=\dfrac{-6}{5}\)
c) \(10\dfrac{2}{9}+\left(2\dfrac{2}{5}-7\dfrac{2}{9}\right)\)
\(=\dfrac{92}{9}+\dfrac{12}{5}-\dfrac{65}{9}\)
\(=\dfrac{92}{9}-\dfrac{65}{9}+\dfrac{12}{5}\)
\(=3+\dfrac{12}{5}\)
\(=\dfrac{15}{5}+\dfrac{12}{5}\)
\(=\dfrac{27}{5}\)
d) \(6\dfrac{3}{10}-\left(3\dfrac{4}{7}+2\dfrac{3}{10}\right)\)
\(=\dfrac{63}{10}-\dfrac{25}{7}-\dfrac{23}{10}\)
\(=\dfrac{63}{10}-\dfrac{23}{10}-\dfrac{25}{7}\)
\(=4-\dfrac{25}{7}\)
\(=\dfrac{28}{7}-\dfrac{25}{7}\)
\(=\dfrac{3}{7}\)
Chúc bạn học tốt

`@` `\text {Ans}`
`\downarrow`
`a)`
\(\left(\dfrac{7}{8}-\dfrac{3}{4}\right)\cdot1\dfrac{1}{3}-\dfrac{2}{3}\cdot0,5\)
`=`\(\dfrac{1}{8}\cdot\dfrac{4}{3}-\dfrac{1}{3}\)
`=`\(\dfrac{1}{6}-\dfrac{1}{3}=-\dfrac{1}{6}\)
`b)`
\(\left(2+\dfrac{5}{6}\right)\div1\dfrac{1}{5}+\left(-\dfrac{7}{12}\right)\)
`=`\(\dfrac{17}{6}\div1\dfrac{1}{5}-\dfrac{7}{12}\)
`=`\(\dfrac{85}{36}-\dfrac{7}{12}=\dfrac{16}{9}\)
`c)`
\(75\%-1\dfrac{1}{2}+0,5\div\dfrac{5}{12}\)
`=`\(-\dfrac{3}{4}+\dfrac{6}{5}=\dfrac{9}{20}\)
a) \(\left(\dfrac{7}{8}-\dfrac{3}{4}\right).1\dfrac{1}{3}-\dfrac{2}{3}.0,5\)
\(=\left(\dfrac{7}{8}-\dfrac{6}{8}\right).\dfrac{4}{3}-\dfrac{2}{3}.\dfrac{1}{2}\)
\(=\dfrac{1}{8}.\dfrac{4}{3}-\dfrac{2}{3}.\dfrac{1}{2}\)
\(=\dfrac{1}{6}-\dfrac{1}{3}\)
\(=\dfrac{-1}{6}\)
b) \(\left(2+\dfrac{5}{6}\right):1\dfrac{1}{5}+\dfrac{-7}{12}\)
\(=\left(\dfrac{12}{6}+\dfrac{5}{6}\right):\dfrac{6}{5}+\dfrac{-7}{12}\)
\(=\dfrac{17}{6}.\dfrac{5}{6}+\dfrac{-7}{12}\)
\(=\dfrac{85}{36}+\dfrac{-7}{12}\)
\(=\dfrac{16}{9}\)
c) \(75\%-1\dfrac{1}{2}+0,5:\dfrac{5}{12}\)
\(=\dfrac{3}{4}-\dfrac{3}{2}+\dfrac{1}{2}.\dfrac{12}{5}\)
\(=\dfrac{3}{4}-\dfrac{6}{4}+\dfrac{6}{5}\)
\(=\dfrac{-3}{4}+\dfrac{6}{5}\)
\(=\dfrac{9}{20}\)

\(150-\left(5.x-25\right)=50\)
\(5.x-25=150-50\)
\(5.x-25=100\)
\(5.x=100+25\)
\(5.x=125\)
\(x=125:5\)
\(x=25\)
150-(5x-25)=50
=>5x-25=150-50=100
=>5x=100+25=125
=>x=125:5=25

a) \(\dfrac{-5}{11}+\left(\dfrac{-6}{11}+1\right)\)
\(=\dfrac{-5}{11}+\left(\dfrac{-6}{11}+\dfrac{11}{11}\right)\)
\(=\dfrac{-5}{11}+\dfrac{5}{11}\)
\(=0\)
b) \(\dfrac{2}{3}+\left(\dfrac{5}{7}+\dfrac{-2}{3}\right)\)
\(=\dfrac{2}{3}+\dfrac{-2}{3}+\dfrac{5}{7}\)
\(=0+\dfrac{5}{7}\)
\(=\dfrac{5}{7}\)
c) \(\left(\dfrac{-1}{4}+\dfrac{5}{8}\right)+\dfrac{-3}{8}\)
\(=\dfrac{-1}{4}+\dfrac{-3}{8}+\dfrac{5}{8}\)
\(=\dfrac{-2}{8}+\dfrac{-3}{8}+\dfrac{5}{8}\)
\(=0\)
d) \(\dfrac{3}{4}.\dfrac{7}{25}+\dfrac{3}{4}.\dfrac{18}{25}\)
\(=\dfrac{3}{4}.\left(\dfrac{7}{25}+\dfrac{18}{25}\right)\)
\(=\dfrac{3}{4}.1\)
\(=\dfrac{3}{4}\)
Chúc bạn học tốt

Ta có 4780 = ( 22 )780 = 21560 = 2120 . 21440
Vì 21440 = ( 212 )120 = 4960120
Nên 4780 = 2120 . 4960120
Mà 14120 = ( 2 . 7 )120 = 2120 . 7120
Vậy 4780 > 14120
4780 và 14120
4780=(413)60=6710886460
14120=(142)60=19660
Vì 6710886460>19660 nên 4780>14120
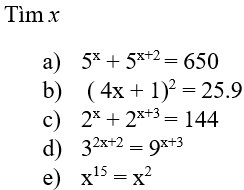
\(x\) + \(\dfrac{1}{10}\) + \(x\) + \(\dfrac{1}{10}\) = \(x\) + \(\dfrac{1}{21}\)
\(x+x\) - \(x\) = \(\dfrac{1}{21}\) - \(\dfrac{1}{10}\) - \(\dfrac{1}{10}\)
\(x\) = \(\dfrac{1}{21}\) - \(\dfrac{1}{5}\)
\(x\) = - \(\dfrac{16}{105}\)