Cho \(a,b,c\ge0;a+b+c=1\). Chứng minh: \(\dfrac{1}{a^2+b^2+c^2}+\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\ge30\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đk: \(-2\le x\le4\)
Ta có \(P^2=\left(\sqrt{x+2}+\sqrt{4-x}\right)^2\)
\(\le2\left[\left(\sqrt{x+2}\right)^2+\left(\sqrt{4-x}\right)^2\right]\) (dùng BĐT \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\))
\(=2\left(x+2+4-x\right)\)
\(=12\)
\(\Rightarrow P\le2\sqrt{3}\) (vì \(P>0\))
Dấu "=" xảy ra \(\Leftrightarrow x+2=4-x\Leftrightarrow x=1\)
Vậy GTLN của P là \(2\sqrt{3}\) khi \(x=1\)
Ta có: \(P=\sqrt{x+2}+\sqrt{4-x}\left(-2\le x\le4\right)\)
\(\Leftrightarrow P^2=\left(\sqrt{x+2}+\sqrt{4-x}\right)^2\)
\(\Leftrightarrow P^2=x+2+4-x+2\sqrt{\left(x+2\right)\left(4-x\right)}\)
\(\Leftrightarrow P^2=6+2\sqrt{\left(x+2\right)\left(4-x\right)}\)
Mà: \(6+2\sqrt{\left(x+2\right)\left(4-x\right)}\le6+x+2+4-x=12\)
\(\Leftrightarrow P^2\le12\)
\(\Leftrightarrow P\le2\sqrt{3}\)
Dấu "=" xảy ra khi: \(x+2=4-x\Leftrightarrow2x=2\Leftrightarrow x=1\)
Vậy: \(P_{max}=2\sqrt{3}\Leftrightarrow x=1\)

Đây là bài toán lãi suất kép trong chương trình 12 chứ ko phải lớp 9

Ta có \(\dfrac{1}{\left(a+1\right)\sqrt{a}+a\sqrt{a+1}}\)
\(=\dfrac{1}{\sqrt{a\left(a+1\right)}\left(\sqrt{a+1}+\sqrt{a}\right)}\)
\(=\dfrac{\sqrt{a+1}-\sqrt{a}}{\sqrt{a\left(a+1\right)}\left(\sqrt{a+1}+\sqrt{a}\right)\left(\sqrt{a+1}-\sqrt{a}\right)}\)
\(=\dfrac{\sqrt{a+1}-\sqrt{a}}{\sqrt{a\left(a+1\right)}}\)
(vì \(\left(\sqrt{a+1}+\sqrt{a}\right)\left(\sqrt{a+1}-\sqrt{a}\right)=\left(a+1\right)-a=1\))
\(=\dfrac{1}{\sqrt{a}}-\dfrac{1}{\sqrt{a+1}}\)
Do đó \(B=\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{99}}-\dfrac{1}{\sqrt{100}}\)
\(=1-\dfrac{1}{10}\)
\(=\dfrac{9}{10}\)

\(\Leftrightarrow\left(x-1\right)^2=27y^3+1\)
\(\Leftrightarrow\left(x-1\right)^2=\left(3y+1\right)\left(9y^2-3y+1\right)\)
Gọi \(d=ƯC\left(3y+1;9y^2-3y+1\right)\)
\(\Rightarrow3y\left(3y^2+1\right)-\left(9y^2-3y+1\right)⋮d\)
\(\Rightarrow6y-1⋮d\)
\(\Rightarrow2\left(3y+1\right)-\left(6y-1\right)⋮d\)
\(\Rightarrow3⋮d\)
Mà \(3y+1⋮d\Rightarrow d\ne3\)
\(\Rightarrow d=1\)
\(\Rightarrow3y+1\) và \(9y^2-3y+1\) nguyên tố cùng nhau
\(\Rightarrow3y+1\) và \(9y^2-3y+1\) đều là SCP
\(\Rightarrow9y^2-3y+1=n^2\)
\(\Leftrightarrow36y^2-12y+4=4n^2\)
\(\Leftrightarrow\left(6y-1\right)^2+3=\left(2n\right)^2\)
\(\Leftrightarrow\left(2n+6y-1\right)\left(2n-6y+1\right)=3\)
\(\Rightarrow y=0\Rightarrow x=\left\{0;2\right\}\)

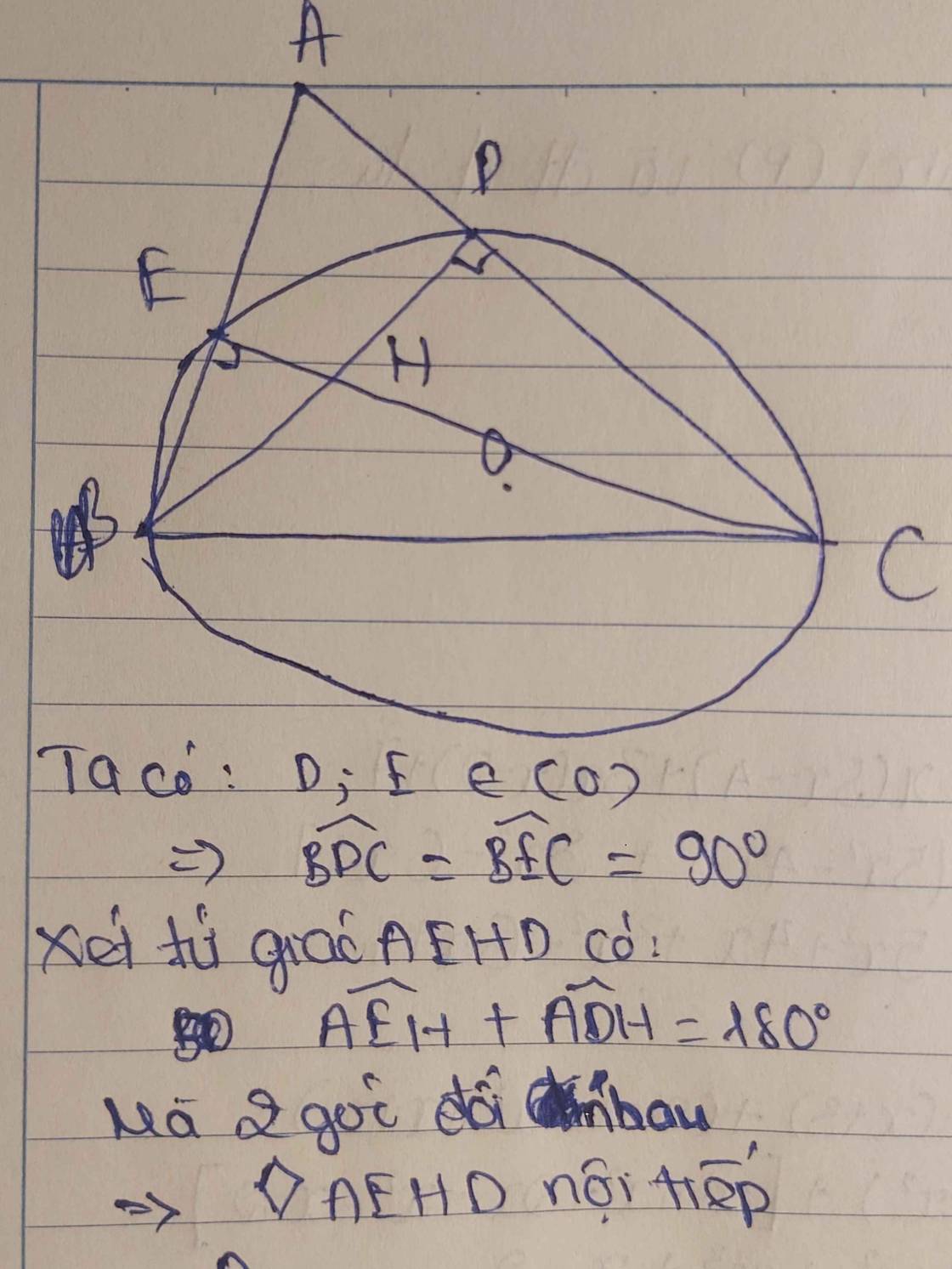
Do BC là đường kính (O) và D thuộc (O) \(\Rightarrow\widehat{BDC}\) là góc nt chắn nửa đường tròn (O)
\(\Rightarrow\widehat{BDC}=90^0\Rightarrow\widehat{BDA}=90^0\)
\(\Rightarrow\widehat{HDA}=90^0\)
Chứng minh tương tự ta có \(\widehat{HEA}=90^0\)
\(\Rightarrow\) 2 điểm D và E cùng nhìn AH dưới 1 góc vuông nên tứ giác ADHE nội tiếp đường tròn đường kính AH

a.
\(sđ\stackrel\frown{AB}=\widehat{AOB}=60^0\)
Do BD là đường kính và A thuộc đường tròn \(\Rightarrow\widehat{DAB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{DAB}=90^0\)
b.
Do B là điểm chính giữa chung AM
\(\Rightarrow sđ\stackrel\frown{AB}=sđ\stackrel\frown{MB}\)
\(\Rightarrow AB=MB\)

Gọi chiều rộng khu vườn là x(m)
(ĐK: x>0)
Chiều dài khu vườn là x+6(m)
Chiều dài khi tăng 5m là x+6+5=x+11(m)
Chiều rộng khu vườn khi tăng thêm 3m là x+3(m)
Diện tích tăng thêm 113m2 nên ta có phương trình:
(x+11)*(x+3)-x(x+6)=113
=>\(x^2+14x+33-x^2-6x=113\)
=>8x=113-33=80
=>x=10(nhận)
Vậy: Chiều rộng ban đầu là 10m
Chiều dài ban đầu là 10+6=16m

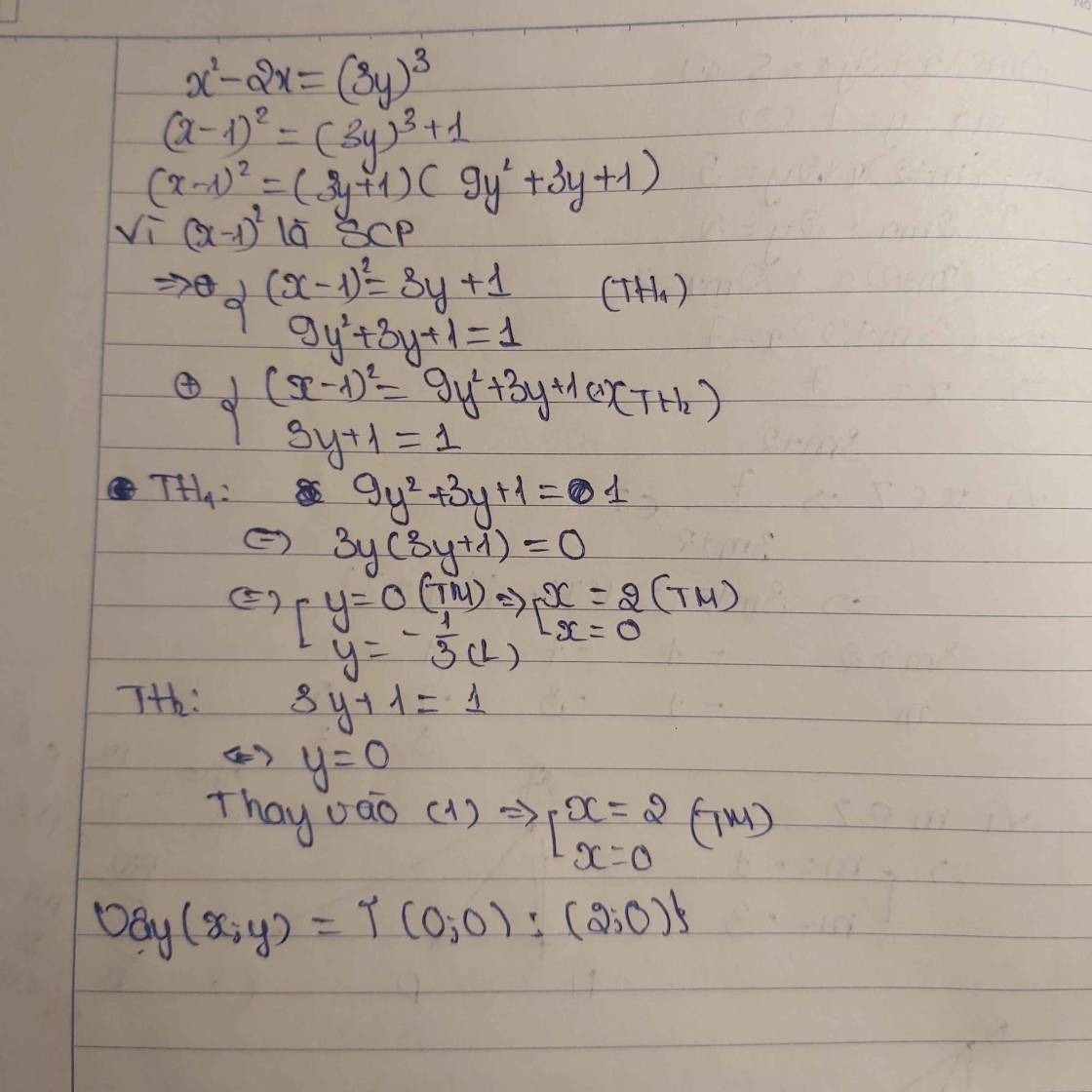

Đề bài chính xác là \(a;b;c>0\) (ko hiểu dấu = có ý nghĩa gì khi mà các mẫu số đều phải khác 0 nên hiển nhiên a;b;c đều khác 0)
Đặt \(P=\dfrac{1}{a^2+b^2+c^2}+\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\)
Do \(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\ge\dfrac{9}{ab+bc+ca}\)
\(\Rightarrow P\ge\dfrac{1}{a^2+b^2+c^2}+\dfrac{9}{ab+bc+ca}\)
\(P\ge\dfrac{1}{a^2+b^2+c^2}+\dfrac{1}{ab+bc+ca}+\dfrac{1}{ab+bc+ca}+\dfrac{7}{ab+bc+ca}\)
\(P\ge\dfrac{9}{a^2+b^2+c^2+2\left(ab+bc+ca\right)}+\dfrac{7}{\dfrac{\left(a+b+c\right)^2}{3}}\)
\(P\ge\dfrac{30}{\left(a+b+c\right)^2}=30\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)