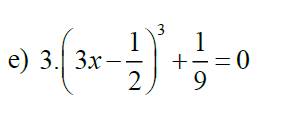
Bài 1:

a: Xét ΔDEI và ΔDFI có

DE=DF

EI=FI

DI chung

Do đó: ΔDEI=ΔDFI

b: Ta có: ΔDEI=ΔDFI

=>\(\widehat{DIE}=\widehat{DIF}\)

mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)

nên \(\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)

=>DI\(\perp\)EF

ΔDEI=ΔDFI

=>\(\widehat{EDI}=\widehat{FDI}\)

=>DI là phân giác của góc EDF

c: Xét ΔIKE vuông tại K và ΔIHF vuông tại H có

IE=IF

\(\widehat{IEK}=\widehat{IFH}\)

Do đó: ΔIKE=ΔIHF

d: ta có: ΔIKE=ΔIHF

=>KE=HF và IK=IH

Ta có: DK+KE=DE

DH+HF=DF

mà DE=DF và KE=HF

nên DK=DH

=>D nằm trên đường trung trực của HK(1)

Ta có: IK=IH

=>I nằm trên đường trung trực của HK(2)

Từ (1),(2) suy ra DI là đường trung trực của HK

=>DI\(\perp\)HK

Xét ΔDEF có \(\dfrac{DK}{DE}=\dfrac{DH}{DF}\)

nên KH//EF

Bài 2:

a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ABC}=90^0-30^0=60^0\)

Xét ΔABD có

AH là đường cao

AH là đường trung tuyến

Do đó: ΔABD cân tại A

Xét ΔABD cân tại A có \(\widehat{ABD}=60^0\)

nên ΔABD đều

b: ΔABD đều

=>\(\widehat{BAD}=\widehat{BDA}=60^0\) và AB=BD=AD

\(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)

=>\(\widehat{CAD}+60^0=90^0\)

=>\(\widehat{CAD}=30^0\)

Xét ΔDCA có \(\widehat{DCA}=\widehat{DAC}\)

nên ΔDAC cân tại D

=>DA=DC

c: Xét ΔDEC vuông tại E và ΔDHA vuông tại H có

DC=DA

\(\widehat{EDC}=\widehat{HDA}\)

Do đó: ΔDEC=ΔDHA

=>AH=CE và DE=DH

d: Xét ΔDEH và ΔDAC có

\(\dfrac{DE}{DA}=\dfrac{DH}{DC}\)

\(\widehat{EDH}=\widehat{ADC}\)

Do đó: ΔDEH~ΔDAC

=>\(\widehat{DEH}=\widehat{DAC}\)

=>EH//AC

a; \(\dfrac{8}{9}\) + \(\dfrac{2}{6}\)  > \(\dfrac{5}{9}\) = \(\dfrac{3}{9}\) + \(\dfrac{2}{9}\)

Vậy \(\dfrac{8}{9}\) + \(\dfrac{2}{6}\) > \(\dfrac{3}{9}\) + \(\dfrac{2}{9}\)

b; \(\dfrac{11}{14}\) > \(\dfrac{10}{14}\) = \(\dfrac{5}{7}\)  = \(\dfrac{3}{7}\) + \(\dfrac{2}{7}\)

Vậy \(\dfrac{11}{14}\) > \(\dfrac{3}{7}\) + \(\dfrac{2}{7}\)

Chu vi vườn hoa đó là:

\(7,5\times2\times3,14=47,1\left(m\right)\)

Số cây cần phải trồng là:

\(47,1:0,3=157\left(cây\right)\) 

Lấy 28 viên bi nkaa

a, \(\dfrac{27}{45}+\dfrac{12}{30}=\dfrac{3}{5}+\dfrac{2}{5}=\dfrac{5}{5}=1\)

b, \(\dfrac{6}{18}+\dfrac{1}{3}=\dfrac{1}{3}+\dfrac{1}{3}=\dfrac{2}{3}\)

a) 27/45 + 12/30

= 3/5 + 2/5

= 5/5 =1.

b) 6/18 + 1/3

=1/3 + 1/3

= 2/3.

\(3\cdot\left(3x-\dfrac{1}{2}\right)^3+\dfrac{1}{9}=0\)

\(\Rightarrow3\cdot\left(3x-\dfrac{1}{2}\right)^3=-\dfrac{1}{9}\)

\(\Rightarrow\left(3x-\dfrac{1}{2}\right)^3=-\dfrac{1}{9}:3\)

\(\Rightarrow \left(3x-\dfrac{1}{2}\right)^3=-\dfrac{1}{27}\)

\(\Rightarrow\left(3x-\dfrac{1}{2}\right)^3=\left(-\dfrac{1}{3}\right)^3\)

\(\Rightarrow3x-\dfrac{1}{2}=-\dfrac{1}{3}\)

\(\Rightarrow3x=-\dfrac{1}{3}+\dfrac{1}{2}\)

\(\Rightarrow3x=\dfrac{1}{6}\)

\(\Rightarrow x=\dfrac{1}{6}:3=\dfrac{1}{18}\)

\(x+\dfrac{13}{15}=-\dfrac{2}{5}\\ x=-\dfrac{2}{5}-\dfrac{13}{15}\\ x=-\dfrac{6}{15}-\dfrac{13}{15}\\ x=-\dfrac{19}{15}\)

\(\dfrac{7}{8}:5\times\dfrac{1}{7}\\ =\dfrac{7}{8}\times\dfrac{1}{5}\times\dfrac{1}{7}\\ =\dfrac{7\times1\times1}{8\times5\times7}\\ =\dfrac{1}{8\times5}=\dfrac{1}{40}\)

Thể tích lượng nước trong bể khi chưa lấy hòn núi giả ra là:

$8\times6\times4=192(dm^3)$

Thể tích lượng nước sau khi lấy hòn núi giả ra là:

$192-19,2=172,8(dm^3)$

Sau khi lấy hòn núi giả ra thì mực nước trong bể cao:

$172,8:8:6=3,6(dm)$