Cho tam giác ABC vuông tại A, đường cao AH. Gọi M là trung điểm của cạnh BC. Hạ HE $\bot$ AB, HF $\bot$ AC.
a) Chứng minh $\dfrac{AF}{CH}= \dfrac{BH}{AC}$;
b) Cho BC cố định, tìm vị trí của A để diện tích hình chữ nhật AEHF lớn nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


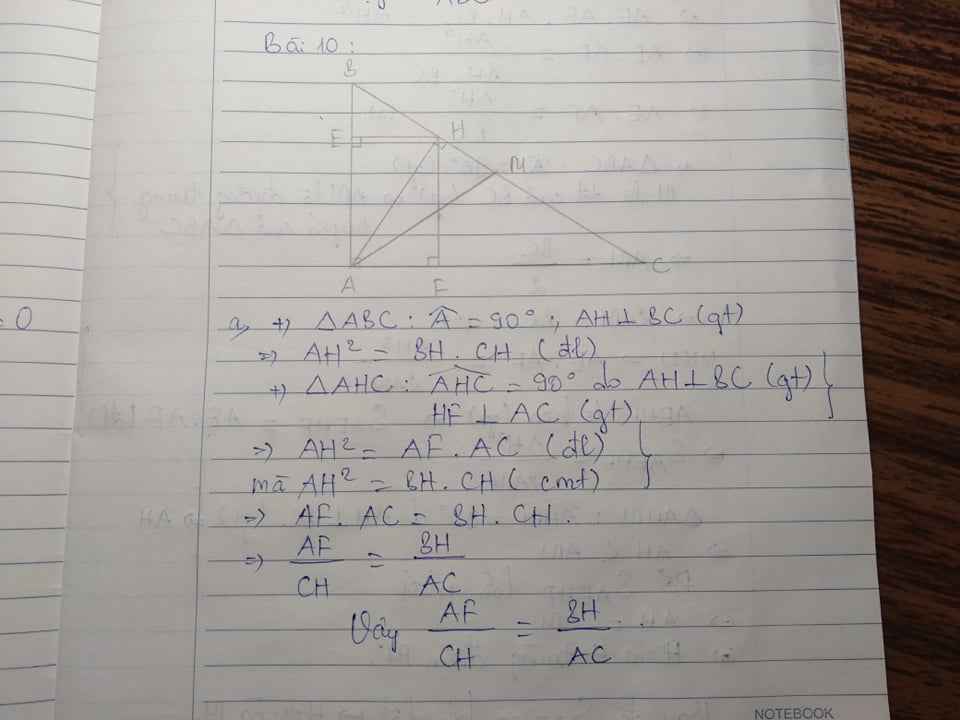


Đặt \(A=\sqrt{x+yz}+\sqrt{y+zx}+\sqrt{z+xy}\)
Ta có:
\(x^2+xy+yz+zx=x+xyz=x\left(x+yz\right)\)
\(\Rightarrow\frac{x\left(x+yz\right)}{x}=\frac{x^2+xy+yz+zx}{x}\)
\(\Leftrightarrow x+yz=\frac{x^2+xy+yz+zx}{x}=\frac{\left(x^2+xy\right)+\left(yz+zx\right)}{x}=\frac{\left(x+z\right)\left(x+y\right)}{x}\)
\(\Rightarrow\sqrt{x+yz}=\sqrt{\frac{\left(x+y\right)\left(x+z\right)}{x}}\)
Vì x, y, z >0 nên áp dụng bất đẳng thức Bunhiacopxki cho 2 số dương, ta được:
\(\left(x+y\right)\left(x+z\right)\ge\left(\sqrt{x^2}.+\sqrt{yz}\right)^2\)
\(\Rightarrow\sqrt{\left(x+y\right)\left(x+z\right)}\ge x+\sqrt{yz}\)
\(\Rightarrow\sqrt{\frac{\left(x+y\right)\left(x+z\right)}{x}}\ge\frac{x+\sqrt{yz}}{\sqrt{x}}\)
Do đó \(\sqrt{x+yz}\ge\frac{x+\sqrt{yz}}{\sqrt{x}}\left(1\right)\)
Chứng minh tương tự, ta được:
\(\sqrt{y+xz}\ge\frac{y+\sqrt{xz}}{\sqrt{y}}\left(2\right)\)
Chứng minh tương tự, ta được:
\(\sqrt{z+xy}\ge\frac{z+\sqrt{xy}}{\sqrt{z}}\left(3\right)\)
Từ (1), (2) và (3), ta được:
\(\sqrt{x+yz}+\sqrt{y+zx}+\sqrt{z+xy}\)\(\ge\frac{x+\sqrt{yz}}{\sqrt{x}}+\frac{y+\sqrt{zx}}{\sqrt{y}}+\frac{z+\sqrt{xy}}{\sqrt{z}}\)
\(\Leftrightarrow A\ge\sqrt{x}+\sqrt{\frac{yz}{x}}+\sqrt{y}+\sqrt{\frac{xz}{y}}+\sqrt{z}+\sqrt{\frac{xy}{z}}\)
\(\Leftrightarrow A\ge\sqrt{x}+\sqrt{y}+\sqrt{z}+\frac{yz+zx+xy}{\sqrt{xyz}}\)
\(\Leftrightarrow A\ge\sqrt{x}+\sqrt{y}+\sqrt{z}+\frac{xyz}{\sqrt{xyz}}\)(vì \(xy+yz+zx=xyz\))
\(\Leftrightarrow A\ge\sqrt{x}+\sqrt{y}+\sqrt{z}+\sqrt{xyz}\)(điều phải chứng minh).
Dấu bằng xảy ra.
\(\Leftrightarrow\hept{\begin{cases}x=y=z>0\\xy+yz+zx=xyz\end{cases}}\Leftrightarrow x=y=z=3\)
Vậy với x, y, z là các số thực dương thỏa mãn xy + yz + zx =xyz thì:
\(\sqrt{x+yz}+\sqrt{y+zx}+\sqrt{z+xy}\ge\sqrt{x}+\sqrt{y}+\sqrt{z}+\sqrt{xyz}\).
\(\)

Đặt 8t=2x
\(d\left(8t\right)=2dx\Rightarrow\frac{d\left(8t\right)}{2}=dx\)
Đổi cận x=0 t=0 x=8 t=2
a , ta có:AE//CF (vì cùng vuông góc vsBD)
=> góc FCO= góc EAO (vì so le trong )
OA = OC (theo t/c hình bh )
xét 2 tam giác vuông OAE và OCF có:
góc FOC = góc EAO ( cm trên )
OA = OC (cmt)
=>tg OAE = tg OCF (cạnh huyền - góc nhọn )
=>OE = OF ( 2 cạnh tương ứng )
b. ta có : AE// CF ( theo a ) (1)
AE = CF ( vì tg OAE= tg OCF ( theo a )) (2)
từ (1) và (2) => AECF là hbh
( hi vọng đúng !!)


thay x=4 vào phương trình tìm ra m rồi lại thay m vào phương trình tìm nghiệm còn lại
cùng dấu thì x1 + x2>0 Khác dấu thì a vs c trái dấu (có a > hoặc = 0 suy ra 4m<0 suy ra m<0 )
x1 x x2>0
Đenta >0

\(A=\left(\sqrt{5}-1\right)\frac{5+\sqrt{5}}{2\sqrt{5}}=\frac{\sqrt{5}\left(5-1\right)}{2\sqrt{5}}=2\)
\(B=\frac{4}{\sqrt{x}+2}-\frac{\sqrt{x}-6}{x+2\sqrt{x}}=\frac{4\sqrt{x}-\sqrt{x}+6}{\sqrt{x}\left(\sqrt{x}+2\right)}=\frac{3\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}\)