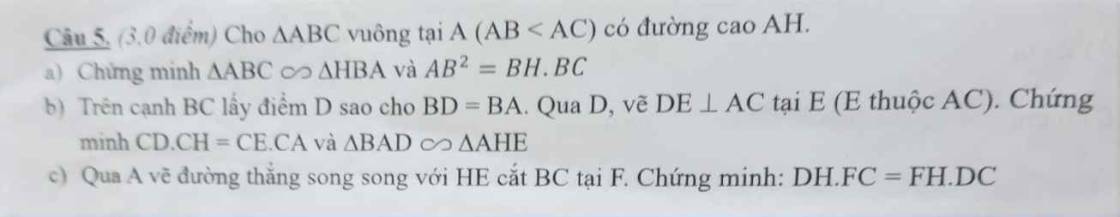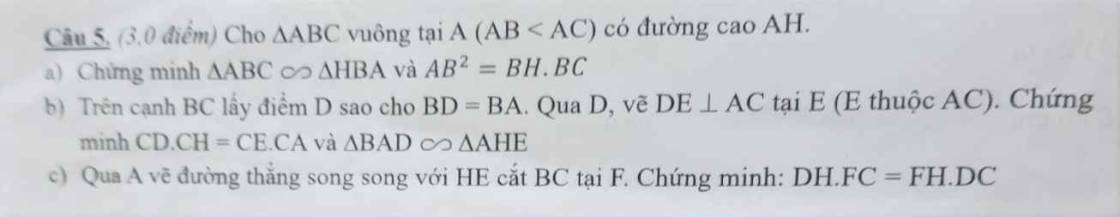Cho tam giác ABC có ba góc nhọn (AB>AC) có 3 đường cao AD, BE, CF cắt nhau tại H.
a) C/M: tam giác BFH đồng dạng tam giác CEH và FA.BH = FH.ACb) Gọi I là trung điểm BC và K là điểm đối xứng của H qua I. C/M: tam giác AKC đồng dạng tam giác AHF
c)AK cắt HC tại O. Lấy điểm M thuộc đoạn thẳng AC sao cho EF//OM. C/M: HM vuông góc AD. C/M giúp em câu c với ạ, em cảm ơn