Một hình chữ nhật có chiều dài 24cm và chu vi bằng 62cm.tính diện tích của hình chữ nhật đó ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 10
Anh Hải đã chạy được quãng đường là:
(225 + 75) × 2 = 600 (m)
Vì 600 m = 600 m nên anh Hải đã đạt được kế hoạch đề ra
Bài 11
Vì 600 m > 500 m nên anh Hải đã đạt được kế hoạch mỗi ngày chạy 500 m

a, Ta có : \(A\left(x\right)=-11x^5+4x-12x^{2^{ }}+11x^5+13x^2-7x+2\\ \Rightarrow A\left(x\right)=x^2-3x+2\)
Ta có: \(M\left(x\right)=A\left(x\right).B\left(x\right)\)
\(\Rightarrow M\left(x\right)=\left(x^2-3x+2\right).\left(x-1\right)\\\Rightarrow M\left(x\right)=x^3-x^2-3x^2+3x+2x-2\\ \Rightarrow M\left(x\right)=x^3-4x^2+5x-2. \)
Vậy...
b) Cho A(x) = 0
x² - 3x + 2 = 0
x² - x - 2x + 2 = 0
(x² - x) - (2x - 2) = 0
x(x - 1) - 2(x - 1) = 0
(x - 1)(x - 2) = 0
x - 1 = 0 hoặc x - 2 = 0
*) x - 1 = 0
x = 0 + 1
x = 1
*) x - 2 = 0
x = 0 + 2
x = 2
Vậy nghiệm của đa thức A(x) là x = 1; x = 2

TH1: chỉ có mặt 3 chữ số 0,3,4
- Chữ số 0 lặp 3 lần: chọn 3 vị trí cho số 0 có \(C_4^3\) cách, xếp 2 chữ số còn lại có 2 cách \(\Rightarrow2.C_4^3\) số
- Chữ số 3 hoặc 4 lặp 3 lần: chọn vị trí cho số 0 có 4 cách, chọn 3 vị trí cho số lặp 2 lần có \(C_4^3\) cách, còn 1 vị trí cho số còn lại \(\Rightarrow2.4.C_4^3\) số
- Chữ số 0 và 3 lặp 2 lần, hoặc 0 và 4 lặp 2 lần: chọn 2 vị trí cho số 0 có \(C_4^2\) cách, chọn vị trí cho 2 số 3 (hoặc 4) có \(C_3^2\) cách \(\Rightarrow2.C_4^2.C_3^2\) số
- Chữ số 3 và 4 lặp 2 lần: chọn vị trí cho số 0 có 4 cách, chọn 2 vị trí cho số 3 có \(C_4^2\) cách, chọn 2 vị trí cho số 4 có \(C_2^2=1\) cách \(\Rightarrow4.C_4^2\) số
TH2: số đã cho có mặt 4 chữ số khác nhau.
Chọn 1 chữ số nữa (từ 1;2;5;6;7;8;9) có 7 cách
- Số 0 lặp 2 lần: chọn 2 vị trí cho số 0 có \(C_4^2\) cách, xếp 3 chữ số còn lại có \(3!\) cách \(\Rightarrow7.C_4^2.3!\) số
- Số 0 có mặt 1 lần: chọn số lặp 2 lần có 3 cách, chọn vị trí cho số 0 có 4 cách, chọn 2 vị trí cho số lặp có \(C_4^2\) cách, hoán vị 2 chữ số còn lại có \(2!\) cách \(\Rightarrow7.3.4.C_4^2.2!\) số
TH3: số đã cho có mặt 5 chữ số khác nhau: chọn 2 chữ số nữa có \(C_7^2\) cách
Hoán vị 5 chữ số: \(5!-4!\) cách \(\Rightarrow C_7^2.\left(5!-4!\right)\) số
Cộng các trường hợp lại được kết quả

Xếp 2 người Việt cạnh nhau: 2 cách
Xếp 3 người Pháp cạnh nhau: \(3!=6\) cách
Với người Nhật, có 2 trường hợp thỏa mãn:
TH1: 4 người Nhật ngồi cạnh nhau: có \(4!\) cách
Hoán vị bộ Nhật - Pháp - Việt có \(3!\) cách
TH2: 4 người Nhật chia làm 2 cặp và 2 cặp này ko ngồi cạnh nhau
Chia 4 người Nhật làm 2 cặp: \(A_4^2.A_2^2=24\) cách (đã xếp thứ tự)
Xếp 2 nhóm Việt và Pháp: \(2!=2\) cách
2 nhóm Việt - Pháp tạo ra 3 khe trống, xếp 2 nhóm người Nhật vào 3 khe trống: \(C_3^2=3\) cách
\(\Rightarrow2.6.\left(4!.3!+24.2.3\right)=3456\) cách

Điều này tương đương ko có cạnh nào của lục giác được tạo ra từ 2 đỉnh liền nhau của đa giác
Chọn 1 đỉnh \(A_1\) có 108 cách
Chọn 5 đỉnh còn lại \(A_2A_3A_4A_5A_6\) sao cho giữa \(A_1A_2\) có \(x_1\) đỉnh, giữa \(A_2A_3\) có \(x_2\) đỉnh, ..., giữa \(A_6A_1\) có \(x_6\) đỉnh với \(x_1;x_2;...;x_6\) là các số nguyên dương
\(\Rightarrow x_1+x_2+x_3+x_4+x_5+x_6=108-6=102\)
Theo nguyên lý chia kẹo Euler, pt trên có \(C_{101}^5\) bộ nghiệm nguyên dương
\(\Rightarrow\dfrac{108.C_{101}^5}{6}\) lục giác thỏa mãn

Số kẹo ban đầu của My là :
5 x \(\dfrac{1}{5}\) = 1 ( cái )
Số kẹo của My sau khi được cho thêm 9 cái là :
9 + 1 = 10 ( cái )
Lúc này tôi có số cái kẹo là :
10 x \(\dfrac{2}{5}\) = 4 ( cái )
Đáp số : 4 cái


Cho phương trình bậc hai \(x^2\) + 2\(x\) - m2 + 2m - 3 = 0
a; Chứng minh phương trình luôn có hai nghiệm phân biệt.
Ta có \(x^2\) + 2\(x\) - m2 + 2m - 3 = 0
⇒ △, = 12 - ( - m2 + 2m - 3) = 1 + m2 - 2m + 3 = (m - 1)2 + 3
(m - 1)2 ≥ 0 ∀ m; ⇒ (m - 1)2 + 3 ≥ 3 ∀ m
⇒△, = (m -1)2 + 3 ≥ 3 > 0 ∀ m
Vậy phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của m.
b; Theo chứng minh trên ta có phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của m, áp dụng hệ thức Vi-et ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1.x_2=-m^2+2m-3\end{matrix}\right.\) (1)
Mặt khác ta có: |\(x_1\) - \(x_2\)| = 4 ⇒ (|\(x_1\) - \(x_2\)|)2 = 42 ⇒ (\(x_1\) - \(x_2\))2 = 16
(\(x_1\) + \(x_2\))2 - 4\(x_2\)\(x_2\) = 16 (2)
Thay (1) vào (2) ta có: (-2)2 - 4.(- m2 + 2m - 3) = 16
4 + 4m2 - 8m + 12 = 16
4m2 - 8m = 16 - 12 - 4
4m2 - 8m = 0
4m.(m - 2) = 0
\(\left[{}\begin{matrix}m=0\\m-2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)
Vậy để phương trình đã cho có hai nghiệm phân biệt thỏa mãn đề bài thì
m \(\in\) {0; 2}
a.
\(\Delta'=1-\left(-m^2+2m-3\right)=m^2-2m+4=\left(m-1\right)^2+3>0;\forall m\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm pb với mọi m
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2+2m-3\end{matrix}\right.\)
\(\left|x_1-x_2\right|=4\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=16\)
\(\Leftrightarrow4-4\left(-m^2+2m-3\right)=16\)
\(\Leftrightarrow m^2-2m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)
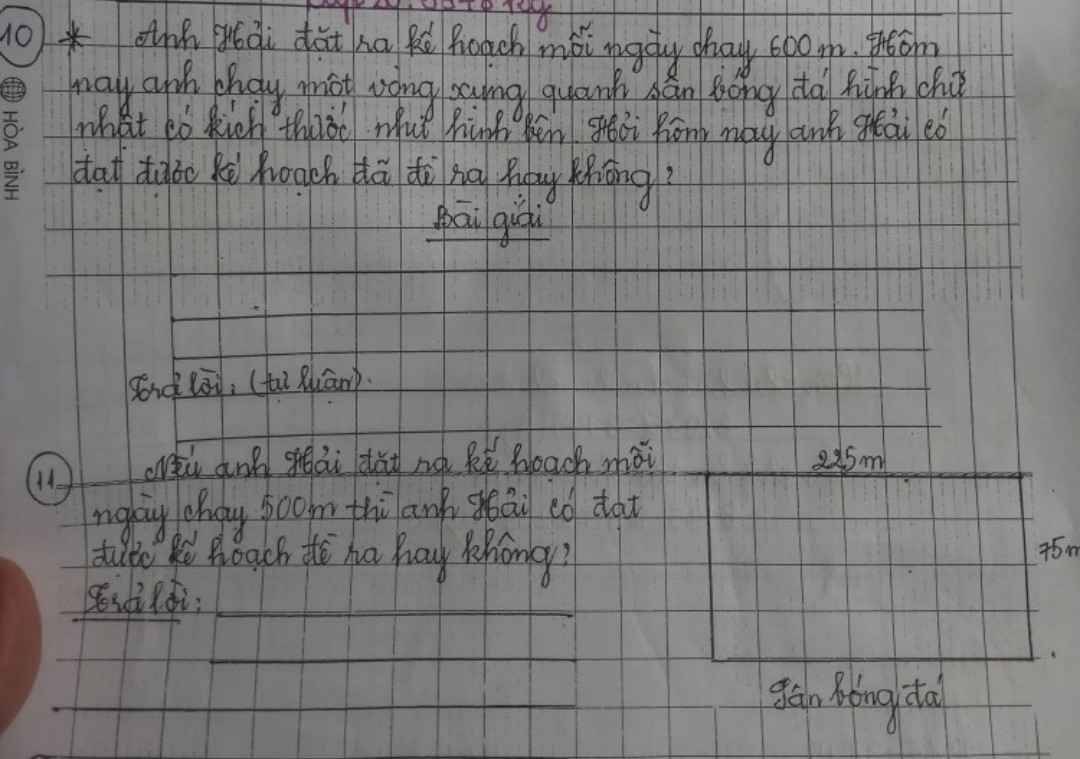
Nửa chu vi hình chữ nhật:
62 : 2 = 31 (cm)
Chiều rộng hình chữ nhật:
31 - 24 = 7 (cm)
Diện tích hình chữ nhật:
31 × 7 = 217 (cm²)