Cho A=1/1x2+1/3x4+1/5x6+1/7x8+...+1/59x60.Chứng tỏ A>7/12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TN
Trần Nguyễn Phương Thảo
CTVHS
VIP
5 tháng 5 2024
\(85-\dfrac{2}{5}=\dfrac{85}{1}-\dfrac{2}{5}=\dfrac{425}{5}-\dfrac{2}{5}=\dfrac{423}{5}\)
KV
5 tháng 5 2024
Số con gà lần đầu bán:
\(152\times\dfrac{3}{8}=57\) (con)
Số con gà lần thứ hai bán:
\(152\times\dfrac{1}{4}=38\) (con)
Số con gà còn lại sau hai lần bán:
\(152-57-38=57\) (con)
KV
5 tháng 5 2024
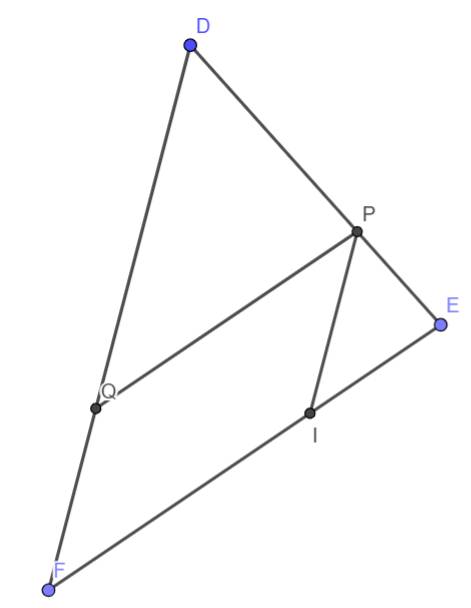
a) Ta có:
\(\dfrac{DP}{DE}=\dfrac{4}{6}=\dfrac{2}{3}\)
\(\dfrac{DQ}{DF}=\dfrac{6}{9}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{DP}{DE}=\dfrac{DQ}{DF}=\dfrac{2}{3}\)
\(\Delta DEF\) có:
\(\dfrac{DP}{DE}=\dfrac{DQ}{DF}=\dfrac{2}{3}\) (cmt)
\(\Rightarrow PQ\) // \(EF\)
\(\Rightarrow\widehat{DPQ}=\widehat{DEF}\) (đồng vị)
Xét \(\Delta DPQ\) và \(\Delta DEF\) có:
\(\widehat{D}\) chung
\(\widehat{DPQ}=\widehat{DEF}\) (cmt)
\(\Rightarrow\Delta DPQ\) ∽ \(\Delta DEF\) (g-g)
b) Sửa đề: Chứng minh \(\Delta EIP\) ∽ \(\Delta PQD\)
Do \(PQ\) // \(EF\) (cmt)
\(\Rightarrow PQ\) // \(FI\)
Do \(PI\) // \(DF\) (gt)
\(\Rightarrow PI\) // \(QF\)
Tứ giác \(FIPQ\) có:
\(PQ\) // \(FI\left(cmt\right)\)
\(PI\) // \(QF\) (cmt)
\(\Rightarrow FIPQ\) là hình bình hành
Do PI // QF (cmt)
\(\Rightarrow\widehat{PIE}=\widehat{QFI}\) (đồng vị)
Do PQ // EF (cmt)
\(\Rightarrow\widehat{DQP}=\widehat{QFI}\) (đồng vị)
Mà \(\widehat{PIE}=\widehat{QFI}\left(cmt\right)\)
\(\Rightarrow\widehat{PIE}=\widehat{DQP}\)
Do PQ // EF (cmt)
\(\Rightarrow\widehat{PEI}=\widehat{DPQ}\) (đồng vị)
Xét \(\Delta EIP\) và \(\Delta PQD\) có:
\(\widehat{PIE}=\widehat{DQP}\) (cmt)
\(\widehat{PEI}=\widehat{DPQ}\left(cmt\right)\)
\(\Rightarrow\Delta EIP\) ∽ \(\Delta PQD\left(g-g\right)\)
6 tháng 5 2024
a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB+6=8
=>AB=2(cm)
b: Vì OA và OM là hai tia đối nhau
nên O nằm giữa A và M
=>AM=AO+OM=6+2=8(cm)
c:
Trên tia Ox, ta có: OI<OB
nên I nằm giữa O và B
=>OI+IB=OB
=>IB+4=8
=>IB=4(cm)
ta có: I nằm giữa O và B
mà IO=IB(=4cm)
nên I là trung điểm của OB
\(A=\dfrac{1}{1.2}+\dfrac{1}{3.4}+\dfrac{1}{5.6}+\dfrac{1}{7.8}+...+\dfrac{1}{59.60}\)
\(A=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{59}-\dfrac{1}{60}\)
\(A=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{60}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+\dfrac{1}{8}+...+\dfrac{1}{60}\right)\)
\(A=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{60}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{30}\right)\)
\(A=\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{60}\)
Ta tách A thành 3 nhóm\(A=\left(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}\right)+\left(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}\right)+\left(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}\right)\)\(A>\dfrac{1}{40}.10+\dfrac{1}{50}.10+\dfrac{1}{60}.10\)
\(A>\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}\)
\(A>\dfrac{37}{60}>\dfrac{7}{12}\)
\(\Rightarrow A>\dfrac{7}{12}\)