a: ta có: BD\(\perp\)AC(ABCD là hình vuông)

BD\(\perp\)SA(SA\(\perp\)(ABCD))

SA,AC cùng thuộc mp(SAC)

Do đó: BD\(\perp\)(SAC)

=>BD\(\perp\)SC

Câu này còn câu b 

Gọi vận tốc thật của cano là x(km/h)

(Điều kiện: x>2)

vận tốc lúc đi là x+2(km/h)

Vận tốc lúc về là x-2(km/h)

\(1h10p=\dfrac{7}{6}\left(giờ\right);1h30p=1,5\left(giờ\right)\)

Độ dài quãng đường lúc đi là \(\dfrac{7}{6}\left(x+2\right)\left(km\right)\)

Độ dài quãng đường lúc về là 1,5(x-2)(km)

Do đó, ta có phương trình:

\(\dfrac{7}{6}\left(x+2\right)=1,5\left(x-2\right)\)

=>\(\dfrac{7}{6}x+\dfrac{7}{3}=1,5x-3\)

=>\(\dfrac{7}{6}x-1,5x=-3-\dfrac{7}{3}\)

=>\(-\dfrac{1}{3}x=-\dfrac{16}{3}\)

=>x=16(nhận)

Vậy: Độ dài quãng đường AB là:

\(\dfrac{7}{6}\left(16+2\right)=\dfrac{7}{6}\cdot18=21\left(km\right)\)

                             Giải

1 giờ 10 phút = \(\dfrac{7}{6}\) giờ; 1 giờ 30 phút = 1,5 giờ

Cứ một giờ ca nô xuôi dòng được: 1 : \(\dfrac{7}{6}\) = \(\dfrac{6}{7}\)(quãng sông)

Cứ một giờ ca nô ngược dòng được: 1 : 1,5  = \(\dfrac{2}{3}\)(quãng sông)

2 km ứng với phân số là: (\(\dfrac{6}{7}\) - \(\dfrac{2}{3}\)): 2 = \(\dfrac{2}{21}\) (quãng sông)

Quãng sông AB dài là: 2 : \(\dfrac{2}{21}\)  = 21 (km)

Kết luận: quãng sông AB dài 21 km. 

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó ΔBAD=ΔBED

b: Xét ΔBKC có

KE,CA là các đường cao

KE cắt CA tại D

Do đó: D là trực tâm của ΔBKC

=>BD\(\perp\)KC

a. Sai

ĐKXĐ: \(n\ge3\) (\(A_n^k\) thì \(n\ge k\), mà k lớn nhất trong ba số  là 3)

b. Sai (câu này coi chừng bị lừa)

\(\dfrac{1}{A_n^2}+\dfrac{1}{A_n^3}\ge\dfrac{1}{C_{n+1}^2}\)

\(\Leftrightarrow\dfrac{\left(n-2\right)!}{n!}+\dfrac{\left(n-3\right)!}{n!}\ge\dfrac{2.\left(n-1\right)!}{\left(n+1\right)!}\)

\(\Leftrightarrow\dfrac{1}{n\left(n-1\right)}+\dfrac{1}{n\left(n-1\right)\left(n-2\right)}\ge\dfrac{2}{\left(n+1\right).n}\)

\(\Leftrightarrow\dfrac{1}{n-1}+\dfrac{1}{\left(n-1\right)\left(n-2\right)}\ge\dfrac{2}{n+1}\)

\(\Leftrightarrow\left(n+1\right)\left(n-2\right)+n+1\ge2\left(n-1\right)\left(n-2\right)\)

\(\Leftrightarrow n^2-6n+5\le0\)

\(\Leftrightarrow1\le n\le5\)

Kết hợp ĐKXĐ \(\Rightarrow3\le n\le5\)  (chỗ này quên kết hợp ĐKXĐ là sẽ chọn sai đáp án) (1)

c. Sai

Từ (1) và n là số tự nhiên \(\Rightarrow n=\left\{3;4;5\right\}\) có 3 nghiệm

d.

\(x^3-12x^2+47x-60=0\Rightarrow x=\left\{3;4;5\right\}\)

Đúng là chung tập nghiệm, nhưng 1 cái biến n 1 cái biến x cứ cấn cấn.

=)) Anh hài ghê

Anh nghỉ sớm nhá anh! Em chúc anh ngủ ngon ạ! < 3  

Đề lỗi hiển thị. Bạn xem lại nhé. 

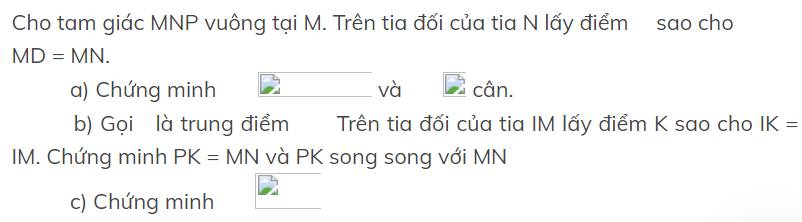
Gọi chiều cao của các tam giác cân màu hồng là x>0

\(\Rightarrow\)  Độ dài đường chéo đáy: \(c=4-2x\)

Do đáy là hình vuông nên cạnh hình vuông: \(a=\dfrac{c}{\sqrt{2}}=\dfrac{4-2x}{\sqrt{2}}=2\sqrt{2}-x\sqrt{2}\)

Cạnh của tam giác cân màu hồng: \(l=\sqrt{\left(\dfrac{4}{2}\right)^2+x^2}=\sqrt{x^2+4}\)

Chiều cao chóp: \(h=\sqrt{l^2-\left(\dfrac{c}{2}\right)^2}=\sqrt{x^2+4-\left(2-x\right)^2}=2\sqrt{x}\)

\(V=\dfrac{1}{3}h.a^2=\dfrac{4}{3}.\sqrt{x}.\left(2-x\right)^2\)

\(\Rightarrow V^2=\dfrac{16}{9}x\left(2-x\right)^4=\dfrac{16}{9}.4x.\left(2-x\right)\left(2-x\right)\left(2-x\right)\left(2-x\right)\)

\(\le\dfrac{16}{9}\left(\dfrac{4x+2-x+2-x+2-x+2-x}{5}\right)^5=\dfrac{16}{9}.\left(\dfrac{8}{5}\right)^5\)

Dấu "=" xảy ra khi \(4x=2-x\Rightarrow x=\dfrac{2}{5}\)

\(\Rightarrow\) Cạnh tam giác cân: \(l=\sqrt{x^2+4}=\sqrt{\left(\dfrac{2}{5}\right)^2+4}=\dfrac{2\sqrt{26}}{5}\)

Lời giải:

a.

$1\frac{2}{5}x=(0,5)^2=0,25$

$1,4x=0,25$

$x=0,25:1,4=\frac{5}{28}$

b.

$2(2x+\frac{2}{3})-\frac{3}{4}=\frac{3}{12}:\frac{1}{2}$

$2(2x+\frac{2}{3})-\frac{3}{4}=\frac{1}{2}$

$2(2x+\frac{2}{3})=\frac{1}{2}+\frac{3}{4}=\frac{5}{4}$

$2x+\frac{2}{3}=\frac{5}{4}:2=\frac{5}{8}$

$2x=\frac{5}{8}-\frac{2}{3}=\frac{-1}{24}$

$x=\frac{-1}{24}:2=\frac{-1}{48}$

Bạn lưu ý lần sau gõ đề bằng công thức toán (nhấn vào biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé. 

a: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có

BD chung

\(\widehat{ABD}=\widehat{MBD}\)

Do đó: ΔBAD=ΔBMD

=>BA=BM

Xét ΔBAM có BA=BM và \(\widehat{ABM}=60^0\)

nên ΔBAM đều

b: ta có: ΔBAM đều

=>\(\widehat{BAM}=\widehat{BMA}=60^0\); MA=MB=AB

\(\widehat{MAB}+\widehat{MAC}=\widehat{BAC}\)

=>\(\widehat{MAC}+60^0=90^0\)

=>\(\widehat{MAC}=30^0\)

ΔBAC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}+60^0=90^0\)

=>\(\widehat{ACB}=30^0\)

Xét ΔMAC có \(\widehat{MAC}=\widehat{MCA}\left(=30^0\right)\)

nên ΔMAC cân tại M

=>\(\widehat{AMC}=180^0-2\cdot\widehat{ACM}=120^0\)

I nằm giữa E và F

=>IE+IF=EF

=>IF+1=7

=>IF=6(cm)

M nằm giữa I và F

=>MI+MF=IF

=>\(\dfrac{1}{3}MF+MF=6\)

=>\(\dfrac{4}{3}MF=6\)

=>\(MF=6:\dfrac{4}{3}=4,5\left(cm\right)\)

Ta có: IM+MF=IF

=>IM+4,5=6

=>IM=1,5(cm)

a Xét ΔAMC và ΔABN có

AM=AB

\(\widehat{MAC}\) chung

AC=AN

Do đó: ΔAMC=ΔABN

b: Gọi K là giao điểm của CM với BN

Ta có: ΔAMC=ΔABN

=>\(\widehat{AMC}=\widehat{ABN}\)

Xét tứ giác AMBK có \(\widehat{AMH}=\widehat{ABH}\)

nên AMBK là tứ giác nội tiếp

=>\(\widehat{BAM}=\widehat{BKM}=90^0\)

=>BN\(\perp\)CM tại K