Có: n + 21 ⋮ n - 2

⇒ n - 2 + 23 ⋮ n - 2

⇒ 23 ⋮ n - 2

⇒ n - 2 ∈ Ư(23)

⇒ n - 2 ∈ {1; 23; -1; -23}

⇒ n ∈ {3; 25; 1; -21}

Vậy: ...

n + 21 chia hết cho n - 2

⇒ n - 2 + 23 chia hết cho n - 2

⇒ n - 2 chia hết cho n - 2 và 23 chia hết cho n - 2

⇒ 23 chia hết cho n - 2

⇒ n - 2 ∈ Ư(23) = {1; -1; 23; -23}

⇒ n ∈ {3; 1; 25; -21} 

Lời giải:
Gọi số vở mà trường đã ủng hộ là $a$ ($600< a< 700$). 

Theo bài ra ta có: 

$a-5\vdots 9,15,7$

$\Rightarrow a-5=BC(9,15,7)$

$\Rightarrow a-5\vdots BCNN(9,15,7)$

$\Rightarrow a-5\vdots 315$

$\Rightarrow a-5\in\left\{0; 315; 630; 945;....\right\}$

$\Rightarrow a\in\left\{5; 320; 635; 950;....\right\}$

Mà $600< a< 700$ nên $a=635$ 

Vậy trường ủng hỗ $635$ quyển vở.

Kết quả là 1638

   3 x 3 x 49 + 90 x 13 + 21 + 6

= 9 x 49 + 1170 + 27

= 441 + 1170 + 27

= 1611 + 27

= 1638

Em xem lại tổng số học sinh nhé!

xin lỗi ạ 42 nhé 

Sửa đề:

13².181 - 5².181 + 144.19

= 169.181 - 25.181 + 144.19

= 181.(169 - 25) + 144.19

= 181.144 + 144.19

= 144.(181 + 19)

= 144.200

= 28800

\(13^2\cdot181-5^2:181+144\cdot19\)

\(=169\cdot181-25:181+144\cdot19\)

\(=30589-\dfrac{25}{181}+2736\)

\(=30588,86188+2736\)

\(=33324,86188\)

$B=1+2+3+4+...+2022+2023$

Số các số hạng của B là:

$(2023-1):1+1=2023$ (số)

Tổng B bằng:

$(2023+1)\cdot2023:2=2047276$

$---$

$C=2+4+6+...+98+100$

Số các số hạng của C là:

$(100-2):2+1=50$ (số)

Tổng C bằng:

$(100+2)\cdot50:2=2550$

$---$

$D=1+3+5+...+97+99$

Số các số hạng của D là:

$(99-1):2+1=50$ (số)

Tổng D bằng:

$(99+1)\cdot50:2=2500$

$---$

$E=10+14+18+...+98+102$

Số các số hạng của E là:

$(102-10):4+1=24$ (số)

Tổng E bằng:

$(102+10)\cdot24:2=1344$

$Toru$

Số lượng số hạng: 

\(\left(2023-1\right):1+1=2023\) (số hạng) 

Tổng B là:

\(B=\left(2023+1\right)\cdot2023:2=2047276\)

_______________

Số lượng số hạng là:

\(\left(100-2\right):2+1=50\) (số hạng)

Tổng C là: 

\(C=\left(100+2\right)\cdot50:2=2550\)

________________

Số lượng số hạng là:

\(\left(99-1\right):2+1=50\) (số hạng)

Tổng D là:

\(D=\left(99+1\right)\cdot50:2=2500\) 

________________

Số lượng số hạng là:

\(\left(102-10\right):4+1=24\) (số hạng)

Tổng E là:

\(E=\left(102+10\right)\cdot24:2=1334\)  

Bạn lưu ý khi đăng câu hỏi thì đăng đầy đủ đề, kèm theo điều kiện của $x,y$.

Trong bài này mình giả sử $x,y$ là các số nguyên.

Tìm $x,y$ thỏa mãn: $(x+3)+y(x+2)=17$

--------------------------

Lời giải:
$(x+3)+y(x+2)=17$

$(x+2)+y(x+2)=16$

$(x+2)(y+1)=16$

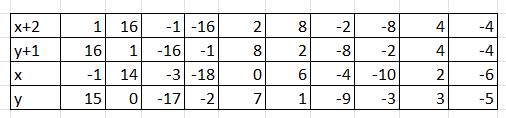
Vì $x+2, y+1$ là các số nguyên với mọi $x,y$ nguyên nên ta có bảng sau:

b sai

6:2(1+2)=6:2.3

               =3.3

               =9

6 : 2 x (1 + 2)

= 3 x 3

= 9.