366=2.3.61

12=2 mũ 2.3

suy ra BCNN=732

ƯCLN=6

Ta có

\(a=12k+9\) (k là số nguyên dương)

\(\Rightarrow a=3\left(4k+3\right)⋮3\)

Ta có

\(a=12k+8+1=4\left(3k+2\right)+1\) => a:4 dư 1 nên a không chia hết cho 4

Do a chia 12 dư 9 nên a = 12k + 9 \(\left(k\in N\right)\)

Ta có:

\(12k⋮3\)

\(9⋮3\)

\(\Rightarrow a=\left(12k+9\right)⋮3\)

Do \(12k⋮4\)

\(9⋮̸4\)

\(\Rightarrow a=\left(12k+9\right)⋮̸4\)

\(3^{x-1}+3^{x+1}-1=89\)

\(3^{x-1}.\left(1+3^2\right)=89+1\)

\(3^{x-1}.10=90\)

\(3^{x-1}=90:10\)

\(3^{x-1}=9\)

\(3^{x-1}=3^2\)

\(x-1=2\)

\(x=2+1\)

\(x=3\)

\(3^{x-1}+3^{x+1}-1=89\)

\(\Rightarrow3^x\cdot\left(3^{-1}+3^1\right)=89+1\)

\(\Rightarrow3^x\cdot\left(\dfrac{1}{3}+3\right)=90\)

\(\Rightarrow3^x\cdot\dfrac{10}{3}=90\)

\(\Rightarrow3^x=90:\dfrac{10}{3}\)

\(\Rightarrow3^x=27\)

\(\Rightarrow3^x=3^3\)

\(\Rightarrow x=3\)

15¹² = 3¹².5¹²

27⁴.25⁶ = (3³)⁴.(5²)⁶ 

27⁴ = 3¹².5¹² 

15¹² = 27⁴.25⁶

27⁴.5⁶ = (3³)⁴.(5²)⁶ = 3¹².5¹² = 15¹²

Vậy 15¹² = 27⁴.5⁶

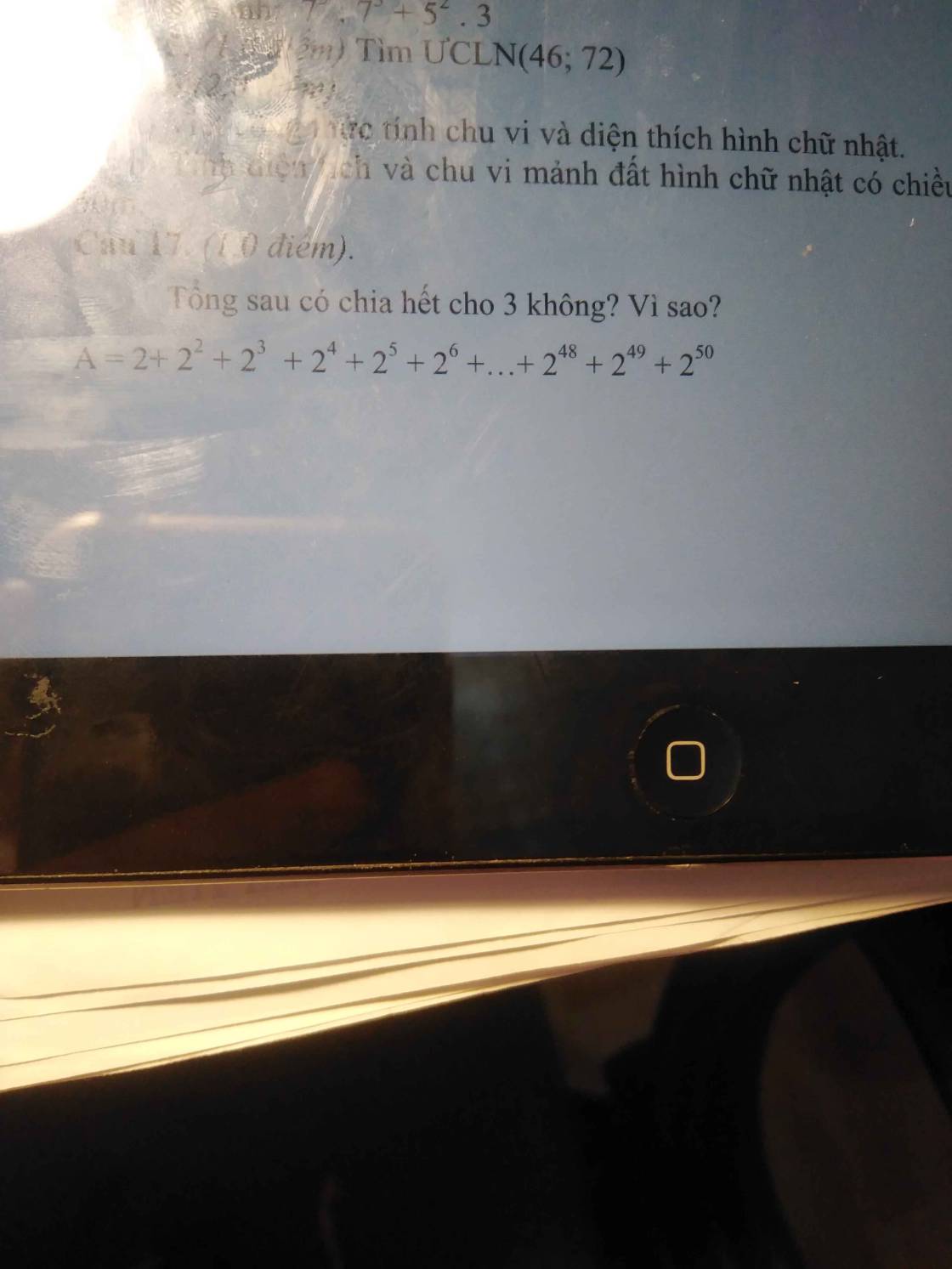
A = 2 + 2² + 2³ + ... + 2⁵⁰

= (2 + 2²) + (2³ + 2⁴) + ... + (2⁴⁹ + 2⁵⁰)

= 2.(1 + 2) + 2³.(1 + 2) + ... + 2⁴⁸.(1 + 2)

= 2.3 + 2³.3 + ... + 2⁴⁹.3

= 3.(2 + 2³ + ... + 2⁴⁹) ⋮ 3

Vậy A ⋮ 3

A = 2 + 2² + 2³+...+2⁵⁰

A = 2¹ + 2² + 2³ +...+ 2⁵⁰

Xét dãy số: 1; 2; 3;...;50 dãy số này có 50 số hạng vậy A có 50 hạng tử

Vì 50 : 2 =  25 nên  ta nhóm hai số liên tiếp của A thành một nhóm thì:

A = (2¹ + 2²) + (2³ + 2⁴) +...+ (2⁴⁹ + 2⁵⁰)

A = 2.(1 + 2) + 2³(1 + 2²) +...+ 2⁴⁹.(1 + 2)

A = 2.3 + 2³.3 +...+ 2⁴⁹.3

A = 3.(2 + 2³ +...+ 2⁴⁹)

Vì 3 ⋮ 3 nên A = 3.(2 + 2³+...+ 2⁴⁹) ⋮ 3 (đpcm)

71:71=1

Vì 71 \(\in\) P nên 

71  = 71

Đổi 360 giây = 6 phút, 420 giây = 7 phút

Giả sử sau x phút họ lại gặp nhau.

Vận động viên thứ nhất chạy một vòng sân hết 6 phút nên x là bội của 6.

Vận động viên thứ hai chạy một vòng sân hết 7 phút nên x là bội của 7.

Suy ra x ∈ BC(6; 7).

Mà x ít nhất nên x = BCNN(6; 7).

6 = 2.3;   7 = 7

  x = BCNN(6; 7) = 2.3.7 = 42

Vậy sau 42 phút họ lại gặp nhau.

123456789×123456789

what!

mọi người giúp mình với , mai mình thi r

giúp mình với mọi người ơi