Từ đề bài ta có

Số thứ nhất chiếm 2 phần

Số thứ hai chiếm 3 phần

Số thứ 2 bằng 1/3 số thứ 3 => Số thứ ba chiếm 9 phần

Số thứ 3 hơn số thứ nhất là: 9-2=7 (phần)

1 phần có giá trị là: 105:7=15

=> Số thứ nhất là: 15x2=30

=> Số thứ hai là: 15x3=45

=> Số thứ ba là: 30+105=135

Vậy 3 số cần tìm là 30, 45, 135

Số phần số thứ 3 hơn số thứ nhất là :
$9-2=7$ ( phần )
Giá trị của 1 phần là :
$105:7=15$
Số thứ nhất là :
$15\times 2=30$

Số thứ 2 là :
$15\times 3=45$
Số thứ 3 là :
$30+105=135$

$\mathrm{Vậy\; ba\; số\; cần\; tìm\; là:}$

• Số thứ nhất: $30$
• Số thứ hai: $45$
• Số thứ ba: $135$
•  

Thời gian ô tô đó đi hết quãng đường AB là:

\(99:45=2,2\) (giờ) = 2 giờ 12 phút

Ô tô đó đi từ A lúc:

11 giờ 12 phút - 2 giờ 12 phút = 9 giờ

9 giờ

Vì 2/5 số hs nam = 3/4 số hs nữ nên 6/15 số hs nam = 6/8 số hs nữ.

Vậy 1/15 số hs nam = 1/8 số hs nữ.

Ta coi số hs nam là 15 phần bằng nhau thì số hs nữ là 8 phần bằng nhau như thế.

Hiệu số phần bằng nhau là:

15-8=7(phần)

Giá trị 1 phần là:

63:7=9(hs)

Số hs nam khối 4 có là:

9x15=135(hs)

Số hs nữ khối 4 có là:

9x8=72(hs)

Đáp số:hs nam:135 hs

             hs nữ:72 hs

(CHÚC BẠN HỌC TỐT!)

Tích cho mik nhé

^^

vì 64=8x8 nên cạnh của 1 hình lập phương là 8cm
V= 8x8x8= 512 (cm3)

                                        Bài giải

Vì 64= 8\(\times\)8 nên suy ra cạnh của hình lập phương là 8cm.

Thể tích của hình lập phương là: 8\(\times\)8\(\times\)8= 512 (cm³)

                                                                 Đáp số: 512 cm³

Lời giải:

Tổng bốn số: $84\times 4=336$ 

Tổng hai số đầu tiên: $336:2=168$
Tổng số thứ ba và số thứ tư: $336-168=168$
Số thứ ba là: $(168-16):2=76$

Số thứ tư là: $76+16=92$

A. S

B. S

C. Đ

D. Đ

a.s

b.s

c.đ

d.đ

nhé tick cho mình nhé

Số học sinh nữ kém hơn số học sinh nam là 8%, xong số học sinh nam là số tròn chục có 2 chữ số bé nhất? Đề có vấn đề bạn coi lại nhé. 

ừ bởi mình cũng ko biêt vì bài này là cô mik mà

0,0005=0,05% Bạn nhé

HỌC TỐT

\(\text{0,0005×100=0,05% }\)

pt thứ hai \(\Leftrightarrow\) \(y^2-\left(3x+2\right)y+2x^2+3x+1=0\) (*)

Ta có \(\Delta=\left[-\left(3x+2\right)\right]^2-4\left(2x^2+3x+1\right)\)

\(=9x^2+12x+4-8x^2-12x-4\)

\(=x^2\ge0\) 

Do đó (*) có 2 nghiệm là \(\left[{}\begin{matrix}y=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3x+2+\sqrt{x^2}}{2}=\dfrac{3x+2+\left|x\right|}{2}\\y=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3x+2-\sqrt{x^2}}{2}=\dfrac{3x+2-\left|x\right|}{2}\end{matrix}\right.\)

Không mất tính tổng quát, giả sử \(x\ge0\). Khi đó:

\(\left[{}\begin{matrix}y=\dfrac{3x+2+x}{2}=\dfrac{4x+2}{2}=2x+1\\y=\dfrac{3x+2-x}{2}=\dfrac{2x+2}{2}=x+1\end{matrix}\right.\)

Nếu \(y=2x+1\) thì thay vào pt đầu tiên, ta có:

\(x^2+\left(2x+1\right)^2+x+2x+1=8\)

\(\Leftrightarrow5x^2+7x-6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\) \(\Rightarrow y=2x+1=2.\dfrac{3}{5}+1=\dfrac{11}{5}\)

Nếu \(y=x+1\) thì thế vào pt đầu tiên, ta có:

\(x^2+\left(x+1\right)^2+x+x+1=8\)

\(\Leftrightarrow2x^2+4x-6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-3\left(loại\right)\end{matrix}\right.\) \(\Rightarrow y=x+1=1+1=2\)

 Vậy ta tìm được 2 cặp nghiệm là \(\left(\dfrac{3}{5},\dfrac{11}{5}\right)\) và \(\left(1,2\right)\)

 Tương tự như vậy, xét TH \(x< 0\) thì ta tìm được thêm 2 cặp nghiệm chính là \(\left(-2,-3\right)\) và \(\left(-3,-2\right)\)

phương trình thứ 2 dấu = ở đâu vậy ạ

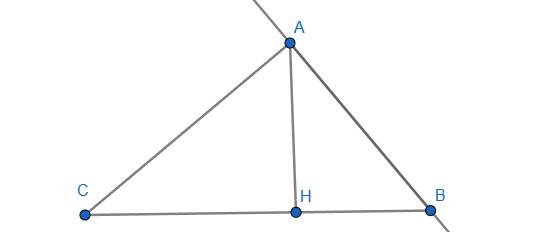
Xét tam giác ABC vuông tại A có AH là đường cao

\(BH.BC=AB^2\)

\(\Rightarrow\left(BC-HC\right)\cdot BC=AB^2\)

\(\Rightarrow\left(BC-19,2\right)\cdot BC=AB^2\)

\(\Rightarrow BC^2-19,2BC=12^2\)

\(\Rightarrow BC^2-19,2BC-144=0\)

\(\Rightarrow BC=\dfrac{48+12\sqrt{41}}{5}\approx24,96\left(cm\right)\)Xét tam giác ABC vuông tại A có

\(BC^2=AB^2+AC^2\)

\(\Rightarrow24,96^2=12^2+AC^2\)

\(\Rightarrow AC\approx21,89\left(cm\right)\)

Xét tam giác ABC vuông tại A có

\(S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}BC.AH\)

\(\Rightarrow\dfrac{1}{2}\cdot12\cdot21,89=\dfrac{1}{2}\cdot24,96\cdot AH\)

\(\Rightarrow AH=\dfrac{262,68}{24,96}\approx10,52\left(cm\right)\)

Vậy độ dài của $AC$ và $AH$ là: $AC\approx 21,89\text{cm và}$ $AH\approx 10,52\text{cm}$

Xét ΔABC vuông tại A có AH là đường cao

nên \(AB^2=BH\cdot BC\)

=>\(BH\left(BH+19,2\right)=12^2=144\)

=>\(BH^2+19,2\cdot BH-144=0\)

=>\(\left[{}\begin{matrix}BH=\dfrac{-19,2-\dfrac{24\sqrt{41}}{5}}{2}\left(loại\right)\\BH=\dfrac{-19,2+\dfrac{24\sqrt{41}}{5}}{2}=-9,6+\dfrac{12\sqrt{41}}{5}\left(nhận\right)\end{matrix}\right.\)

=>\(BH=\dfrac{-48+12\sqrt{41}}{5}\)

=>\(BC=\dfrac{-48+12\sqrt{41}}{5}+19,2=\dfrac{48+12\sqrt{41}}{5}\left(cm\right)\)

ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC=\dfrac{-48+12\sqrt{41}}{5}\cdot19,2=3,84\left(-48+12\sqrt{41}\right)\)

=>\(AH=\sqrt{3,84\left(-48+12\sqrt{41}\right)}\left(cm\right)\)

=>\(AC=\sqrt{AH^2+HC^2}=\sqrt{3,84\left(-48+12\sqrt{41}\right)+19,2^2}\)

=>\(AC=\sqrt{184,32+46,08\sqrt{41}}\)(cm)