chua kip tra loi đa bat nop bai
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Chiều dài là: (85 + 15) : 2 = 50 (cm)
Chiều rộng của hình chữ nhật là: 85 - 50 = 35 (cm)
Diện tích của hình chữ nhật là: 50 x 35 = 1750 (cm\(^2\))
Đáp số: 1750\(\operatorname{cm}^2\)

246 x 79 - 246 - 246 x 68
= 246 x 79 - 246 x 1 - 246 x 68
= 246 x (79 - 1 - 68)
= 246 x (78 - 68)
= 246 x 10
= 2460
246x79-246-246x68
=246x79-246x1-246x68
=246x(79-68-1)
=246x10
=2460

Giải:
Số lượng mì chính mà mẹ đã mua là:
2000g x 150 = 300 000 (g)
300 000 g = 300 kg
Đáp số: 300 kg
Trong trường hợp mẹ mua về bán thì bài toán này là hợp lí, còn nếu mua về ăn thì nó không có tính khoa học, vì không thể sử dụng hết lượng mì chính đã mua cho một gia đình trong hạn sử dụng của nó

\(-\dfrac{5}{6}\le\dfrac{x}{9}\le-\dfrac{1}{9}\\ -\dfrac{15}{18}\le\dfrac{2x}{18}\le-\dfrac{2}{18}\\=>-15\le2x\le-2\\ =>-\dfrac{15}{2}\le x \le-1\\ =>-7,5\le x\le-1\\ =>x\in\left\{-7;-6;-5;-4;-3;-2;-1\right\}\)
- \(\frac56\) ≤ \(\frac{x}{9}\) ≤ - \(\frac19\) (\(x\in\) Z)
\(\frac{-15}{18}\) ≤ \(\frac{2x}{18}\) ≤ \(\frac{-2}{18}\)
- 15 ≤ 2\(x\) ≤ - 2
- \(\frac{15}{2}\) ≤ \(x\) ≤ \(\frac{-2}{2}\)
- 7\(\frac12\) ≤ \(x\) ≤ - 1
Vì \(x\in\) Z nên
\(x\) \(\in\) {-7; -6; -5; -4; -3; -2; -1}
Vậy \(x\in\left\lbrace-7;-6;-5;-4;-3;-2;-1\right\rbrace\)

Câu b:
(n + 25) ⋮ (n + 5) (n ≠ - 5)
[(n + 5) + 20] ⋮ (n + 5)
20 ⋮ (n + 5)
(n +5) ∈ Ư(20)
20 = 2\(^2\).5 suy ra
(n + 5) \(\in\) Ư(20) = {-20; - 10; - 5; -4; -2; -1; 1; 2; 4; 5; 10; 20}
Lập bảng giá trị ta có:
n+5 | -20 | -10 | -5 | -4 | -2 | -1 | 1 | 2 | 4 | 5 | 10 | 20 |
n | -25 | -15 | -10 | -9 | -7 | -6 | -4 | -3 | -1 | 0 | 5 | 15 |
Theo bảng trên ta có:
n ∈ {-25; -15; -10; -9; -7; -6; -4; -3; -1; 0; 5; 15}
Câu a:
(14 + 6n) ⋮ n
14 ⋮ n
n ∈ Ư(14)
14 =2.7 suy ra: n ∈ Ư(14) = {-14; -7; -2; -1; 1; 2; 7; 14}
Vậy n ∈ {-14; -7; -2; -1; 1; 2; 7; 14}

Câu 1:
x2−4x+3=0x^2 - 4x + 3 = 0x2−4x+3=0
Phương trình này là phương trình bậc hai có dạng chuẩn ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0 với:
- a=1a = 1a=1, b=−4b = -4b=−4, c=3c = 3c=3.
Tính biệt số Δ\DeltaΔ:
Δ=b2−4ac=(−4)2−4(1)(3)=16−12=4.\Delta = b^2 - 4ac = (-4)^2 - 4(1)(3) = 16 - 12 = 4.Δ=b2−4ac=(−4)2−4(1)(3)=16−12=4.
Vì Δ>0\Delta > 0Δ>0, phương trình có hai nghiệm phân biệt:
x=−b±Δ2a=4±22.x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{4 \pm 2}{2}.x=2a−b±Δ=24±2.
Suy ra hai nghiệm:
x1=4−22=1,x2=4+22=3.x_1 = \frac{4 - 2}{2} = 1, \quad x_2 = \frac{4 + 2}{2} = 3.x1=24−2=1,x2=24+2=3.
Vậy nghiệm của phương trình là x=1x = 1x=1 hoặc x=3x = 3x=3.
Câu 2
Phương trình:
x2−2(m−1)x+m2−m−4=0x^2 - 2(m-1)x + m^2 - m - 4 = 0x2−2(m−1)x+m2−m−4=0
Có hai nghiệm phân biệt khi:
Δ′=(m−1)2−(m2−m−4)>0.\Delta' = (m-1)^2 - (m^2 - m - 4) > 0.Δ′=(m−1)2−(m2−m−4)>0.
Tính toán:
m2−2m+1−m2+m+4>0.m^2 - 2m + 1 - m^2 + m + 4 > 0.m2−2m+1−m2+m+4>0. −m+5>0.- m + 5 > 0.−m+5>0. m<5.m < 5.m<5.
Ta có điều kiện:
x12−2x2(x2−2)+m2−5m=0.x_1^2 - 2x_2(x_2 - 2) + m^2 - 5m = 0.x12−2x2(x2−2)+m2−5m=0.
Sử dụng định lý Vi-ét
x1+x2=2(m−1),x_1 + x_2 = 2(m-1),x1+x2=2(m−1), x1x2=m2−m−4.x_1 x_2 = m^2 - m - 4.x1x2=m2−m−4.
Dùng đẳng thức:
x12=(x1+x2)2−2x1x2.x_1^2 = (x_1 + x_2)^2 - 2x_1 x_2.x12=(x1+x2)2−2x1x2.
Thay vào:
(2(m−1))2−2(m2−m−4)−2x2(x2−2)+m2−5m=0.(2(m-1))^2 - 2(m^2 - m - 4) - 2x_2(x_2 - 2) + m^2 - 5m = 0.(2(m−1))2−2(m2−m−4)−2x2(x2−2)+m2−5m=0.
Biến đổi:
4(m−1)2−2(m2−m−4)−2x22+4x2+m2−5m=0.4(m-1)^2 - 2(m^2 - m - 4) - 2x_2^2 + 4x_2 + m^2 - 5m = 0.4(m−1)2−2(m2−m−4)−2x22+4x2+m2−5m=0.
Dùng x22=(x1+x2)2−2x1x2x_2^2 = (x_1 + x_2)^2 - 2x_1x_2x22=(x1+x2)2−2x1x2, thay vào:
4(m−1)2−2(m2−m−4)−2[(2(m−1))2−2(m2−m−4)]+4x2+m2−5m=0.4(m-1)^2 - 2(m^2 - m - 4) - 2[(2(m-1))^2 - 2(m^2 - m - 4)] + 4x_2 + m^2 - 5m = 0.4(m−1)2−2(m2−m−4)−2[(2(m−1))2−2(m2−m−4)]+4x2+m2−5m=0.
Rút gọn:
4(m2−2m+1)−2m2+2m+8−2[4(m2−2m+1)−2m2+2m+8]+4x2+m2−5m=0.4(m^2 - 2m + 1) - 2m^2 + 2m + 8 - 2[4(m^2 - 2m + 1) - 2m^2 + 2m + 8] + 4x_2 + m^2 - 5m = 0.4(m2−2m+1)−2m2+2m+8−2[4(m2−2m+1)−2m2+2m+8]+4x2+m2−5m=0.
Sau khi tiếp tục biến đổi và rút gọn, ta giải phương trình để tìm các giá trị mmm thỏa mãn.
Kết quả cuối cùng là m=3m = 3m=3 (thỏa mãn cả hai điều kiện trên).


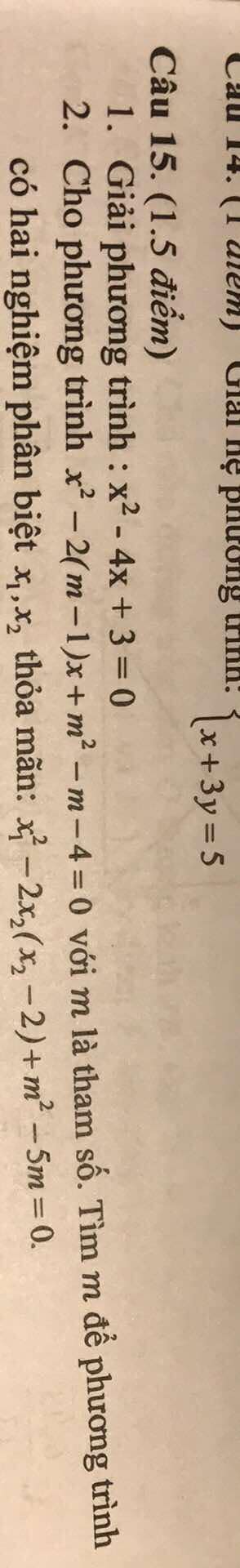
ok!
bye!bye!☺