Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a.\dfrac{3}{7}=\dfrac{2x+1}{3x+5}\\ 3\left(3x+5\right)=7\left(2x+1\right)\\ 9x+15=14x+7\\ 14x-9x=15-7\\ 5x=8\\ x=\dfrac{8}{5}\\ b.\dfrac{x+1}{x-2}=\dfrac{3}{4}\\ 3\left(x-2\right)=4\left(x+1\right)\\ 3x-6=4x+4\\ 4x-3x=-6-4\\ x=-10\\ c.\dfrac{2x+3}{7}=\dfrac{4x-1}{15}\\ 15\left(2x+3\right)=7\left(4x+1\right)\\ 30x+45=28x+7\\ 30x-28x=7-45\\ 2x=-38\\ x=\dfrac{-38}{2}=-19\\ d.\dfrac{6x-5}{-7}=\dfrac{5x-3}{-5}\\ -5\left(6x-5\right)=-7\left(5x-3\right)\\ -30x+25=-35x+21\\ -30x+35x=21-25\\ 5x=-4\\ x=-\dfrac{4}{5}\)

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
a) \(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{bk}{b\left(k+1\right)}=\dfrac{k}{k+1}=\dfrac{dk}{d\left(k+1\right)}=\dfrac{dk}{dk+d}=\dfrac{c}{c+d}\)
b) \(\dfrac{2a+5b}{3a-4b}=\dfrac{2bk+5b}{3bk-4b}=\dfrac{b\left(2k+5\right)}{b\left(3k-4\right)}=\dfrac{2k+5}{3k-4}=\dfrac{d\left(2k+5\right)}{d\left(3k-4\right)}=\dfrac{2dk+5d}{3dk-4d}=\dfrac{2c+5d}{3c-4d}\)
c) \(\dfrac{2018a-2019b}{2019c+2020d}=\dfrac{2018bk-2019b}{2019dk+2020d}=\dfrac{b\left(2018k-2019\right)}{d\left(2019k+2020\right)}=\dfrac{b}{d}\cdot\dfrac{2018k-2019}{2019k+2020}\) (1)
Mà: \(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{b}{d}=\dfrac{c}{a}\)
\(\left(1\right)=\dfrac{c}{a}\cdot\dfrac{2018k-2019}{2019k+2020}=\dfrac{2018ck-2019c}{2019ak+2020a}=\dfrac{2018ck-2019dk}{2019ak+2020bk}\\ =\dfrac{k\left(2018c-2019d\right)}{k\left(2019a+2020b\right)}=\dfrac{2018c-2019d}{2019a+2020b}\)

(5.3^5) + 17.3^4) : 6^2
= (5.243 + 17.81) : 36
= (1215 + 1377) : 36
= 2592 : 36
= 72

\(x^2-64\cdot0,5\cdot x+3=0\\ \Leftrightarrow x^2-32x+256=253\\ \Leftrightarrow x^2-32x+16^2=253\\ \Leftrightarrow\left(x-16\right)^2=253\\ \Leftrightarrow\left[{}\begin{matrix}x-16=\sqrt{253}\\x-16=-\sqrt{253}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\sqrt{253}+16\\x=-\sqrt{253}+16\end{matrix}\right.\)
Vậy...

a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB+2=6
=>AB=4(cm)
b: M là trung điểm của OB
=>\(OM=BM=\dfrac{OB}{2}=3\left(cm\right)\)
Trên tia Ox, ta có: OA<OM(2cm<3cm)
nên A nằm giữaO và M
=>OA+AM=OM
=>AM+2=3
=>AM=1(cm)
a) OA < OB => A nằm giữa O và B
=> AB = OB - OA = 6 - 2 = 4(cm)
b) M là trung điểm của OB =>` OM=MB=1/2OB=1/2*6=3(cm) `
=> AM=AB - MB = 4 - 3 = 1(cm)

M(x)=P(x)-Q(x)
\(=-6x^5-4x^4+3x^2-2x-2x^5+4x^4+2x^3+2x^2+x+3\)
\(=-8x^5+2x^3+5x^2-x+3\)
\(M\left(-1\right)=-8\left(-1\right)^5+2\cdot\left(-1\right)^3+5\cdot\left(-1\right)^2-\left(-1\right)+3\)
=8-2+5+1+3
=6+6+3
=15

a: Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{B}+\widehat{C}=180^0-75^0=105^0\)
mà \(\widehat{B}-\widehat{C}=15^0\)
nên \(\widehat{B}=\dfrac{105^0+15^0}{2}=60^0;\widehat{C}=60^0-15^0=45^0\)
b: BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{60^0}{2}=30^0\)
Xét ΔABD có \(\widehat{ABD}+\widehat{BAD}+\widehat{ADB}=180^0\)
=>\(\widehat{ADB}+30^0+75^0=180^0\)
=>\(\widehat{ADB}=75^0\)

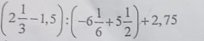
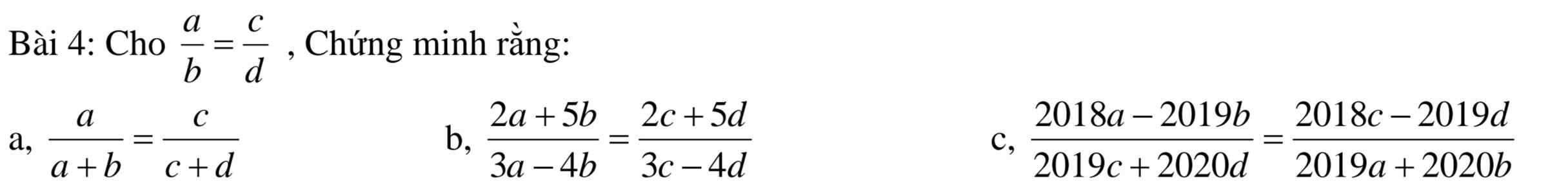


a: \(0,5^{1000}=\left(0,5^5\right)^{200}=0,03125^{200}\)
mà \(0,03125< 0,625\)
nên \(0,5^{1000}< 0,625^{200}\)
c: \(A=2+2^2+...+2^{2022}\)
=>\(2A=2^2+2^3+...+2^{2023}\)
=>\(2A-A=2^2+2^3+...+2^{2023}-2-2^2-...-2^{2022}\)
=>\(A=2^{2023}-2\)
=>A<B
e: \(2020A=\dfrac{2020^{2024}-2020}{2020^{2024}-1}=1-\dfrac{2019}{2020^{2024}-1}\)
\(2020B=\dfrac{2020^{2024}+2020}{2020^{2024}+1}=1+\dfrac{2019}{2020^{2024}+1}\)
Vì \(-\dfrac{2019}{2020^{2024}-1}< 0< \dfrac{2019}{2020^{2024}+1}\)
nên \(-\dfrac{2019}{2020^{2024}-1}+1< \dfrac{2019}{2020^{2024}+1}+1\)
=>2020A<2020B
=>A<B
d: \(\left(-\dfrac{3}{2}\right)^{2024}=\left(\dfrac{3}{2}\right)^{2024};\left(-2\right)^{2024}=2^{2024}\)
mà 3/2<2
nên \(\left(-\dfrac{3}{2}\right)^{2024}< 2^{2024}\)