lực hút của mặt trăng lên một vật đặt trên mặt trăng chỉ bằng 1/6 trọng lượng của vật đó. lực hút của mặt trăng lên một nhà du hành vũ trụ có khối lượng 81 kg đang ở trên mặt trăng là bao nhiêu?
giải thành lời giúp mình với!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu trả lời:
a) Khi hai gương phẳng đặt vuông góc với nhau (90∘), một điểm sáng S giữa hai gương sẽ tạo ra 3 ảnh. Đây là do:
Vậy tổng cộng có 3 ảnh được tạo ra.
b) Khi hai gương phẳng G1 và G2 đặt song song, tia sáng tới SI phản xạ lần lượt trên G1 và G2. Để tính góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên G2, ta sử dụng các nguyên tắc quang học:
Do đó, tổng góc giữa tia tới SI ban đầu và tia phản xạ cuối cùng được tính dựa trên hình học của các gương.

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

Để giải bài toán này, ta cần tính thời gian xe A đi từ A đến G, sau đó dùng thời gian này để tính vận tốc cần thiết của xe B trong hai trường hợp.
Vậy, trong cả hai trường hợp, vận tốc cần thiết của xe B để gặp xe A tại điểm G cùng một lúc là 40 km/h.
a; chuyển động cùng chiều:
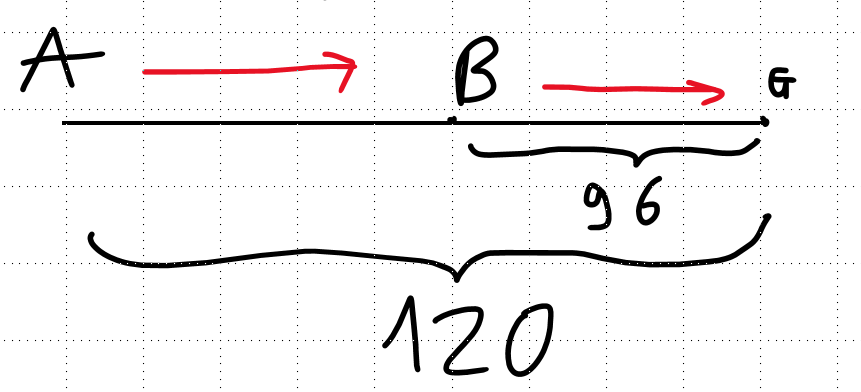
đoạn đường AB là: \(s_{AB}=s_{AG}-s_{BG}=120-96=24\left(km\right)\)
Thời gian ô tô đi từ A đến chỗ gặp là: \(t_A=\dfrac{s_{AG}}{v_A}=\dfrac{120}{50}=2,4\left(giờ\right)\)
Quãng đường xe đi từ A đến chỗ gặp cách A là: \(s_A=v_1t=50t\left(1\right)\)
Quãng đường xe đi từ B đến chỗ gặp cách A là: \(s_B=v_2t+24\left(2\right)\)
Từ (1) (2) ⇒ \(50\cdot2,4=v_2\cdot2,4+24⇒\:v_2=40\left(km\text{/}h\right)\)
b; chuyển động ngược chiều:
Thời gian xe A đi đến chỗ gặp là: \(t_A=\dfrac{s_{AG}}{v_{AG}}=\dfrac{120}{50}=2,4\left(\text{giờ}\right)\) (4)
Thời gian xe B đi đến chỗ gặp là: \(t_B=\dfrac{s_{BG}}{v_{BG}}=\dfrac{96}{v_{BG}}\left(3\right)\)
Mà thời gian đi đến chỗ gặp là bằng nhau nên từ (3) (4) ta có
\(\dfrac{96}{v_{BG}}=2,4⇒\:v_{BG}=40\left(km\text{/}h\right)\)
vậy: .....

Trả lời:
Sự chuyển hóa về lực là quá trình lực này sinh ra hoặc biến đổi thành lực khác thông qua các tương tác vật lý. Ví dụ, khi bạn kéo một vật bằng dây, lực kéo của bạn truyền qua dây tạo thành lực căng dây, lực này lại tác dụng lên vật làm vật chuyển động. Trong máy móc, lực do động cơ tạo ra có thể chuyển hóa thành lực ma sát, lực đàn hồi, hoặc lực nâng, tùy vào cơ cấu truyền lực. Sự chuyển hóa này tuân theo định luật bảo toàn năng lượng: lực không tự sinh ra hoặc mất đi mà chỉ chuyển từ dạng này sang dạng khác hoặc từ vật này sang vật khác.

Khi thả viên bi làm nó chuyển động->Tạo ra thế năng(từ trên cầu tuột xuống) rồi thành động năng và nhiệt năng (lực ma sát giữa viên bi và cầu tuột).

Trả lời:
Động cơ thường (không turbo) | Động cơ có turbo (turbocharged) |
|---|---|
Không có bộ tăng áp | Có bộ tăng áp (turbo) |
Không tận dụng khí xả để tăng công suất | Sử dụng khí xả để quay turbo, nén khí nạp |
Công suất thấp hơn so với cùng dung tích | Công suất cao hơn, tiết kiệm nhiên liệu hơn |
Phản ứng ga mượt, độ trễ thấp | Có thể có độ trễ turbo (turbo lag) |
Cấu tạo đơn giản, chi phí bảo dưỡng thấp | Cấu tạo phức tạp, chi phí bảo dưỡng cao hơn |
mình kiếm bài mẫu cho bạn thôi nhé:
Trọng lượng của nhà du hành vũ trụ trên Trái Đất là:
75,5 . 10 = 755 (N)
Trọng lượng của nhà du hành vũ trụ trên Mặt Trăng là:
755.16=7556≈125,83755 . 16=7556≈125,83 (N)
Vậy trọng lượng của nhà du hành vũ trụ trên Mặt Trăng là 125,83 N.