Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Ứng dụng tích phân để tính thể tích vật thể SVIP
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a, x=b. Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức nào?
Cho hình phẳng D giới hạn bởi đồ thị y=(2x−1)lnx, trục hoành và đường thẳng x=e.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Diện tích hình phẳng D=21∫1∣(2x−1)lnx∣dx. |
|
| b) Diện tích hình phẳng D=0∫e∣(2x−1)lnx∣dx. |
|
| c) Thể tích V khối tròn xoay tạo thành khi quay hình phẳng D quanh trục Ox: V=π1∫e(2x−1)2lnxdx. |
|
| d) Thể tích V khối tròn xoay tạo thành khi quay hình phẳng D quanh trục Ox: V=π21∫e(2x−1)2lnxdx. |
|
Cho hình phẳng (H) giới hạn bởi các đường y=x+11,y=0,x=0,x=2. Quay hình phẳng (H) quanh trục hoành tạo nên một khối tròn xoay có thể tích bằng
Gọi D là phần hình phẳng giới hạn bởi các đường x=−1;y=0;y=x3. Thể tích khối tròn xoay tạo nên khi quay D quanh trục Ox bằng
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y=−x, đường thẳng y=−x+2 và trục hoành.
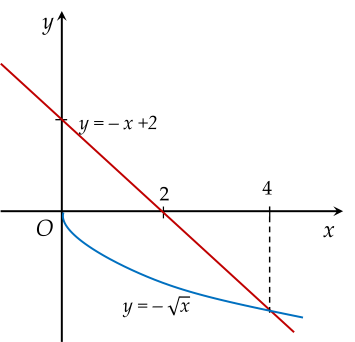
Khối tròn xoay tạo ra khi (H) quay quanh Ox có thể tích V được xác định bằng công thức nào sau đây?
Hình phẳng (H) giới hạn bởi các đường y=x2+1, trục tung và tiếp tuyến của đồ thị hàm số y=x2+1 tại điểm (1;2). Khi quay hình (H) quanh trục Ox tạo thành khối tròn xoay có thể tích V bằng
Cho hàm số y=f(x)=ax3+bx2+cx+d(a,b,c,d∈R) có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y=4 tại điểm có hoành độ âm và đồ thị hàm số y=f′(x) cho bởi hình vẽ dưới đây:
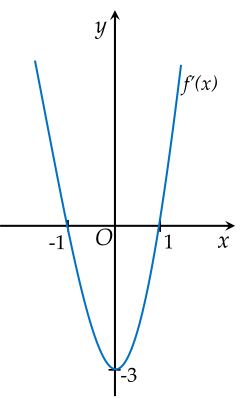
| a) Hàm số y=f(x) có điểm cực tiểu tại x=0. |
|
| b) Hàm số y=f(x) nghịch biến trên khoảng (−1;1) |
|
| c) Hàm số y=f(x)=x3−3x−2. |
|
| d) Thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giới hạn bởi đồ thị (C) và trục hoành khi quay xung quanh trục Ox là 35729π |
|
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y=x,y=0 và x=4 quanh trục Ox. Đường thẳng x=a(0<a<4) cắt đồ thị hàm số y=x tại M (hình vẽ). Gọi V1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox, trong đó H(4;0). Tìm a sao cho V=2V1.

Trả lời:
Gọi (H) là hình phẳng giới hạn bởi parabol y=x2−4x+4, đường thẳng y=4x−12 và trục hoành. Biết thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục hoành bằng baπ(a,b là các số nguyên dương và ba là phân số tối giản). giá trị của a+b bằng
Cho (H) là hình phẳng giới hạn bởi 41 cung tròn có bán kính R=2, đường cong y=4−x và trục hoành, x=3.
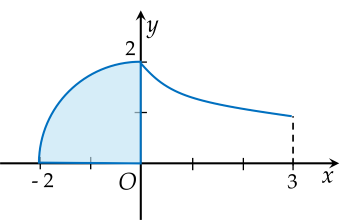
| a) Công thức tính diện tích hình quạt trên hình theo tích phân là −2∫04−x2dx |
|
| b) Diện tích hình phẳng (H) gần bằng 6,5. |
|
| c) Thể tích nửa khối cầu bán kính R=2 là 16π. |
|
| d) Thể tích V khối tạo thành khi cho (H) quay quanh Ox là 677π. |
|

Bạn có thể đăng câu hỏi về bài học này ở đây
