Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tự luận SVIP
(2,0 điểm).
Biểu đồ trong hình bên biểu diễn số tiền đầu tư vào mỗi vùng Đồng bằng sông Hông (ĐBSH) và Đông bằng sông Cửu Long (ĐBSCL) của công ty An Bình trong bốn quý năm 2021. Em hãy cho biết:
a) Biểu đồ đã sử dụng là loại biểu đồ nào sau đây: biểu đồ cột, biểu đồ cột kép, biểu đồ đoạn thẳng, biểu đồ hình quạt tròn.
b) Đối tượng thống kê là gì? Tiêu chí thống kê là gì?
c) Lập bảng số liệu thống kê số tiên đầu tư vào vùng ĐBSH và vùng ĐBSCL của công ty An Bình trong bốn quý năm 2021 theo mẫu sau.
Số tiền công ty An Bình đầu tư vào vùng ĐBSH và vùng ĐBSCL năm 2021.
| Quý | 1 | 2 | 3 | 4 |
| Số tiền đầu tư vào vùng ĐBSH (tỉ đồng) | ? | ? | ? | ? |
| Số tiền đầu tư vào vùng ĐBSCL (tỉ đồng) | ? | ? | ? | ? |
d) Quý nào tổng mức đầu tư của công ty An Bình vào hai vùng kinh tế ĐBSH và ĐBSCL là cao nhất?
e) Trong năm 2021, công ty An Bình đã đầu tư vào vùng kinh tế nào nhiều hơn?
Hướng dẫn giải:
a) Biểu đồ đã sử dụng là biểu đồ cột kép.
b) -Đối tượng thống kê là vùng ĐBSH, vùng ĐBSCL, quý 1, quý 2, quý 3 , quý 4.
-Tiêu chí thống kê là số tiền công ty An Bình đã đầu tư.
c) Công ty An Bình đâu tư vào vùng ĐBSH và vùng ĐBSCL năm 2021.
| Quý | $1$ | $2$ | $3$ | $4$ |
| Số tiền đầu tư vào vùng ĐBSH (tỉ đồng) | $62$ | $55$ | $35$ | $61$ |
| Số tiền đầu tư vào vùng ĐBSCL (tỉ đồng) | $78$ | $45$ | $25$ | $35$ |
d)
| Quý | $1$ | $2$ | $3$ | $4$ |
| Số tiền đầu tư vào vùng ĐBSH (tỉ đồng) | $62$ | $55$ | $35$ | $61$ |
| Số tiền đầu tư vào vùng ĐBSCL (tỉ đồng) | $78$ | $45$ | $25$ | $35$ |
| Số tiền đầu tư vào cả hai vùng (tỉ đồng) | $140$ | $100$ | $60$ | $96$ |
Tổng mức đầu tư của công ty vào cả hai vùng cao nhất trong quý $1$.
e) Năm 2021, tổng mức đầu tư của công ty vào ĐBSH là $62+55+35+61=213$ tỷ đồng; tổng mức đầu tư của công ty vào ĐBSCL là $78+45+25+35=183$ tỉ đồng. Công ty đã đầu tư vào ĐBSH nhiều hơn.
Lãi suất tiên gửi ngân hàng kì hạn 1 năm của một ngân hàng là $x \%$. Một người gửi vào ngân hàng đó $300$ triệu đồng theo phương thức lãi nhập gốc, tức là đến kì đáo hạn nếu người gửi không rút lãi thì toàn bộ số tiền lãi sẽ được nhập vào tiền vốn cho kì tiếp theo.
a) Viết đa thức $A$ biểu diễn số tiền người đó nhận được (cả gốc lẫn lãi) sau khi gửi 1 năm.
b) Viết đa thức $B$ biểu diễn số tiền người đó nhận được (cả gốc lẫn lãi) sau khi gửi 2 năm.
c) Viết đa thức $C$ biểu diễn số tiền người đó nhận được (cả gốc lẫn lãi) sau khi gửi 2 năm.
d) Nếu lãi suất năm của ngân hàng là $6\%$ thì sau 1 năm, 2 năm, 3 năm khi rút cả gốc lẫn lãi người gửi nhận được bao nhiêu tiền?
Hướng dẫn giải:
a) (0,5 điểm)
| Gốc (triệu đồng) | Lãi (triệu đồng) | Gốc+Lãi (triệu đồng) |
| $300$ | $300.x:100=3x$ | $300+3x$ |
Sau 1 năm, người đó nhận được (nếu rút cả gốc lẫn lãi)
$A=3x+300$ (triệu đồng)
b) (0,5 điểm)
| Gốc (triệu đồng) | Lãi (triệu đồng) | Gốc+Lãi (triệu đồng) |
| $A=3x+300$ | $A.x:100=0,03x^2+3x$ | $0,03x^2+6x+300$ |
Sau 2 năm, người đó nhận được (nếu rút cả gốc lẫn lãi)
$B=0,03x^2+6x+300$ (triệu đồng)
c) (0,5 điểm)
| Gốc (triệu đồng) | Lãi (triệu đồng) | Gốc+Lãi (triệu đồng) |
| $B=0,03x^2+6x+300$ | $B.x:100=0,0003x^3+0,06x^2+3x$ | $0,0003x^3+0,09x^2+9x+300$ |
Sau 3 năm, người đó nhận được (nếu rút cả gốc lẫn lãi)
$C=0,0003x^3+0,09x^2+9x+300$ (triệu đồng)
d) (0,5 điểm)
Nếu lãi suất năm của ngân hàng là $6 \%$ thì $x=6$. Số tiền người đó nhận được khi rút cả gốc lẫn lãi sau 1 năm là giá trị của $A$ tại $x=6$ và bằng $318$ triệu.
Tương tự, nếu rút cả gốc và lãi sau 2 năm thì người đó được nhận $337,08$ triệu đồng.
Nếu rút cả gốc và lãi sau 3 năm thì người đó được nhận $357,3048$ triệu đồng.
(2,0 điểm).
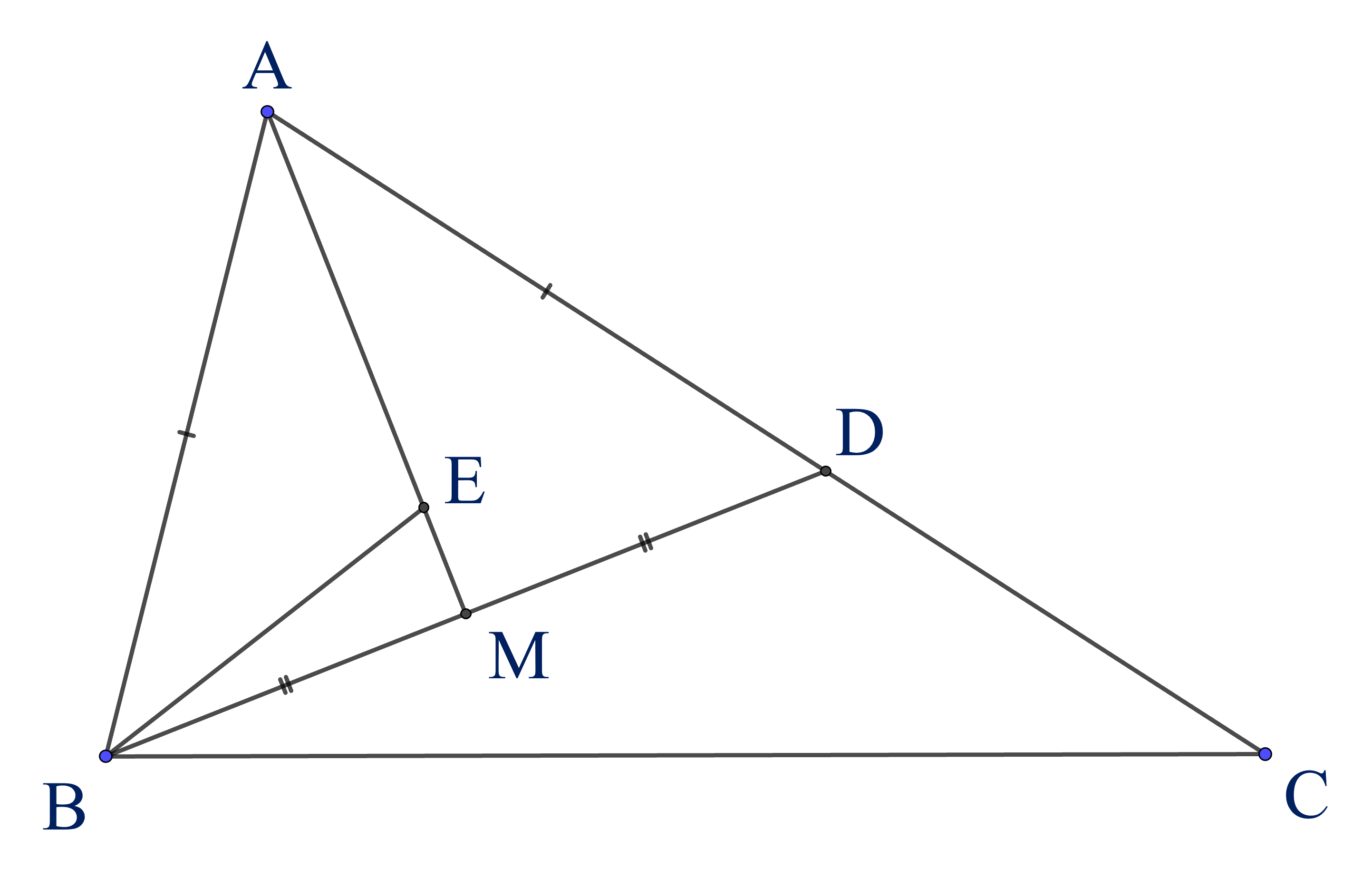
Cho tam giác $ {ABC}$ có $ {AB}< {AC}$. Trên cạnh $ {AC}$ lấy điểm $ {D}$ sao cho $ {AD}= {AB}$. Gọi $ {M}$ là trung điểm của $B D$; $E$ là giao điểm của tia phân giác góc $B$ với tia $A M$.
a)(1,25 điểm) Chứng minh rằng tia $ {AM}$ là tia phân giác góc $ {A}$ của tam giác $ {ABC}$.
b)(0,75 điểm) Cho góc $C$ có số đo bằng $30^{\circ}$. Hãy tính số đo góc $ACE$.
Hướng dẫn giải:
a)(0,5 điểm)
b) (0,75 điểm)
Xét $\triangle A D M$ và $\triangle A B M$ có $A D=A B$ (giả thiết); $D M=B M$ (giả thiết $M$ là trung điểm của $B D$ ); $A M$ chung. Suy ra $\triangle A D M=\triangle A B M$ (c.c.c).
Do đó $\widehat{D A M}=\widehat{B A M}$ (góc tương ứng). Vì vậy $A M$ là tia phân giác góc $A$ của tam giác $A B C$.
c) (0,75 điểm)
Theo chứng minh trên, có $A M$ là tia phân giác góc $A$. Lại có $ {E}$ là giao điểm của tia phân giác góc $ {B}$ với tia $ {AE}$ (giả thiết).
Như vậy $E$ là giao điểm của tia phân giác góc $ {A}$ với tia phân giác góc $ {B}$. Suy ra $CE$ là phân giác góc $C$ (theo định lí: ba đường phân giác của tam giác đồng quy tại một điểm).
Từ đó $\widehat{A C E}=\dfrac{1}{2} \widehat{C}=15^{\circ}$.
(0,5 điểm)
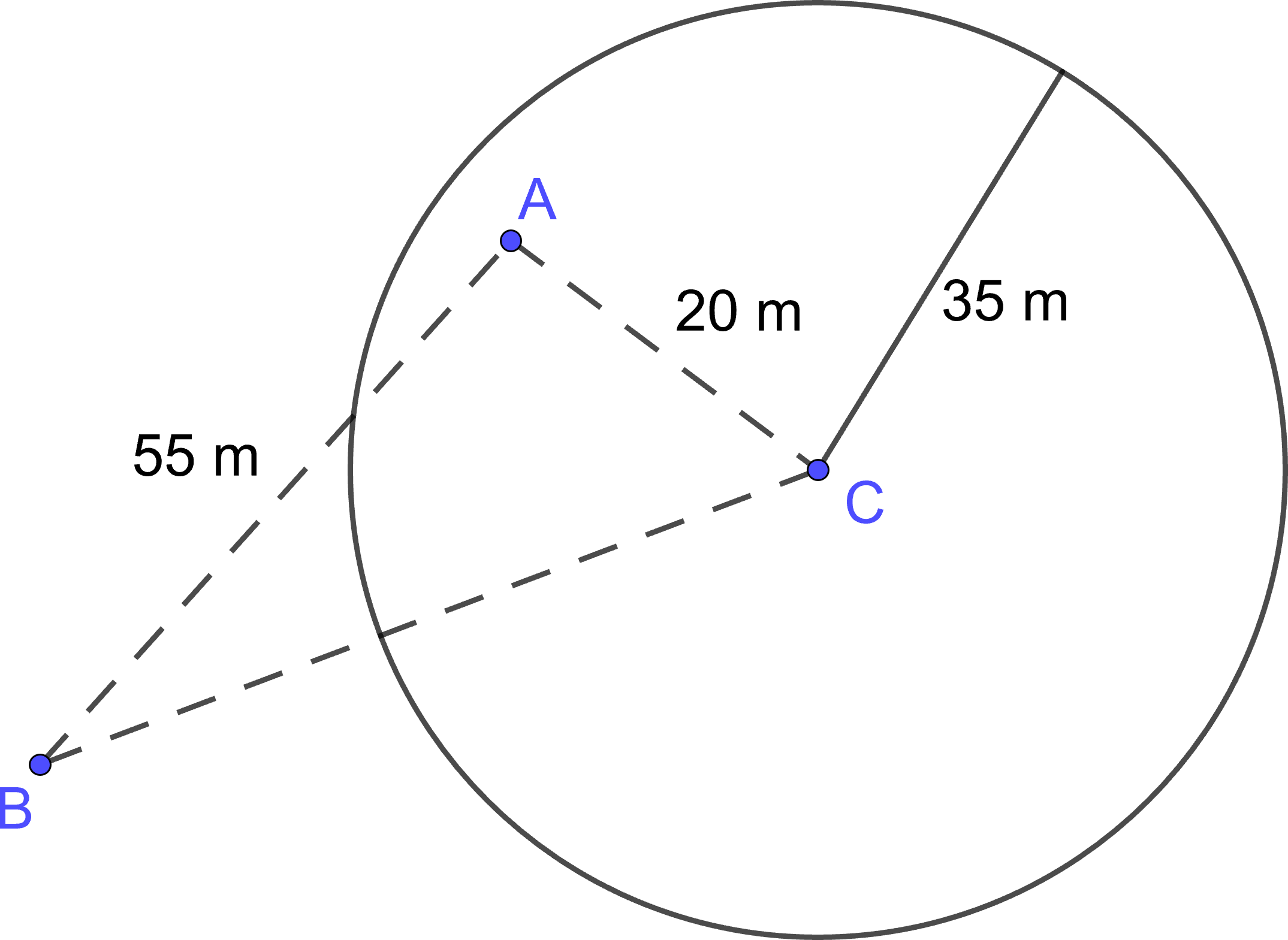
Ông A và ông B đứng cách nhau $55$ mét. Một bộ phát wifi có bán kính hoạt động $35$ mét và cách ông A $20$ mét. Em hãy cho biết điện thoại di động của ông A hay ông B không nhận được sóng wifi? Vì sao?
Hướng dẫn giải:
(Không yêu cầu vẽ hình).
Kí hiệu A, B là vị trí ông A và ông B đang đứng. C là vị trí bộ phát wifi.
Trong $\Delta ABC$ có $BC>AB-AC=55-20=35$.
Suy ra khoảng cách từ ông B đến vị trí bộ phát wifi lớn hơn bán kính hoạt động của bộ phát. Do đó ông B không nhận được sóng wifi.
Khoảng cách từ ông A đến bộ phát wifi là $20$ m(nhỏ hơn bán kính hoạt động của bộ phát) nên ông A nhân được sóng wifi.
