Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tự luận SVIP
($2$ điểm).
Theo công bố chính thức từ hãng sản xuất, xe ô tô của ông An có mức tiêu thụ nhiên liệu cho mỗi $100$ km trên các loại đường như sau:
| Đường hỗn hợp | Đường đô thị | Đường cao tốc |
| $9,9$ lít | $13,9$ lít | $7,5$ lít |
a)($0,5$ điểm) Để đi được $30$ km đường đô thị, xe của ông An cần tối thiểu bao nhiêu lít xăng?
b)($0,5$ điểm) Với $4,17$ lít xăng, xe của ông An chạy được tối đa bao nhiêu kilômét đường cao tốc?
c)($1$ điểm) Ông An lái xe đi từ nhà về quê. Từ nhà ra đến đường cao tốc, ông An phải lái xe $20$ km đường đô thị. Sau đó khi chạy tiếp $80$ km đường cao tốc, ông An còn phải chạy tiếp $30$ km đường hỗn hợp. Em hãy tính xem xe của ông An tiêu thụ hết bao nhiêu lít xăng?
Hướng dẫn giải:
($2$ điểm).
a)($0,5$ điểm) Khi xe di chuyển trên cùng một loại đường thì chiều dài quãng đường tỉ lệ thuận với lượng xăng tiêu thụ. Ta có bảng tóm tắt sau:
| Loại đường đô thị |
Chiều dài quãng $(km)$ |
Lượng xăng tiêu thụ ($l$) |
| $100$ | $13,9$ | |
| $30$ | $x$ |
Từ đó $x=(30.13,9): 100=4,17$. Do đó, để đi được $30$ km đường đô thị cần tối thiểu $4,17$ lít xăng.
b)($0,5$ điểm) Tương tự, ta có
| Loại đường cao tốc |
Chiều dài quãng $(km)$ |
Lượng xăng tiêu thụ ($l$) |
| $100$ | $7,5$ | |
| $y$ | $4,17$ |
Do đó $y=(100.4,17): 7,5=55,6$. Nếu đi trên cao tốc thì với $4,17$ lít xăng, xe chạy được $55,6$ km.
c)($1$ điểm) Bài toán được tóm tắt như sau:
| Loại đường | Chiều dài quãng (km) |
Lượng xăng tiêu thụ (l) |
| Đô thị | $100$ | $13,9$ |
| $20$ | $x$ | |
| Cao tốc | $100$ | $7,5$ |
| $80$ | $y$ | |
| Hỗn hợp | $100$ | $9,9$ |
| $30$ | $z$ |
Từ đó $x=(20.13,9): 100=2,78 ; \quad y=(80.7,5): 100=6 ; z=(30.9,9): 100=$ $2,97$.
Do đó từ nhà về quê, xe ông An tiêu thụ hết:
$2,78 +6+2,97=11,75$ lít xăng.
(1,5 điểm).
Một bể chứa nước có dạng hình hộp chữ nhật được thiết kế với chiều rộng, chiều dài, chiều cao tỉ lệ với ba số $3 ; 2 ; 1$. Người ta mở một vòi cho nước vào bể. Gọi $x$ (dm) là chiều cao của bể.
a)(1 điểm) Hãy viết đa thức biểu thị số lít nước cần phải thêm vào bể để bể đầy nước, biết rằng trong bể đang có $100$ lít nước.
b)(0,5 điểm) Tính thời gian vòi chảy đầy bể trong trường hợp chiều cao bể là $5$ dm và mỗi phút vòi chảy được $25$ lít nước.
Hướng dẫn giải:
a) (1 điểm)
Chiều rộng, chiều dài, chiều cao của bể lần lượt là $2x;\,3x;\,x$.
Bể có thể tích $2x.3x.x=6x^3$ (dm$^3$).
Bể chứa được $6x^3$ lít nước. Do bể đang có $100$ lít nước nên để bể đầy nước cần thêm vào bể $A=6x^3-100$ (lít) nước.
b) (0,5 điểm)
Trường hợp bể có chiều cao $5$ dm thì $x=5$, lượng nước cần thêm vào bể là giá trị của đa thức $A$ tại $x=5$, tức là $6.5^3-100=625$ (lít)
Để đầy nước, cần mở vòi trong $625:25=25$ phút.
(1,0 điểm).
Trong một cửa hàng bán các suất ăn nhanh, mỗi suất gồm một món chính và một món phụ với thực đơn như sau
| Món chính | Món phụ |
| Cánh gà rán; đùi gà rán; phở | Khoai tây chiên; phô mai que |
Bạn Hải gọi ngẫu nhiên một suất đủ hai món. Tính xác suất xảy ra biến cố A: "Hải chọn suất ăn gồm đùi gà rán và phô mai que".
Hướng dẫn giải:
Xét $6$ biến cố sau:
A: "Hải chọn suất ăn gôm đùi gà rán và phô mai que".
B: "Hải chọn suất ăn gôm đùi gà rán và khoai tây chiên".
C: "Hải chọn suất ăn gồm cánh gà rán và phô mai que".
D: "Hải chọn suất ăn gồm cánh gà rán và khoai tây chiên".
E: "Hải chọn suất ăn gồm phở và phô mai que".
F: "Hải chọn suất ăn gồm phở và khoai tây chiên".
Ta thấy $6$ biến cố trên đồng khả năng và luôn xảy ra đúng một trong sáu biến cố này.
Vì vậy, mỗi biến cố trên đều có xác suất bằng $\dfrac{1}{6}$. Nói riêng, biến cố A có xác suất bằng $\dfrac{1}{6}$.
(2,0 điểm).
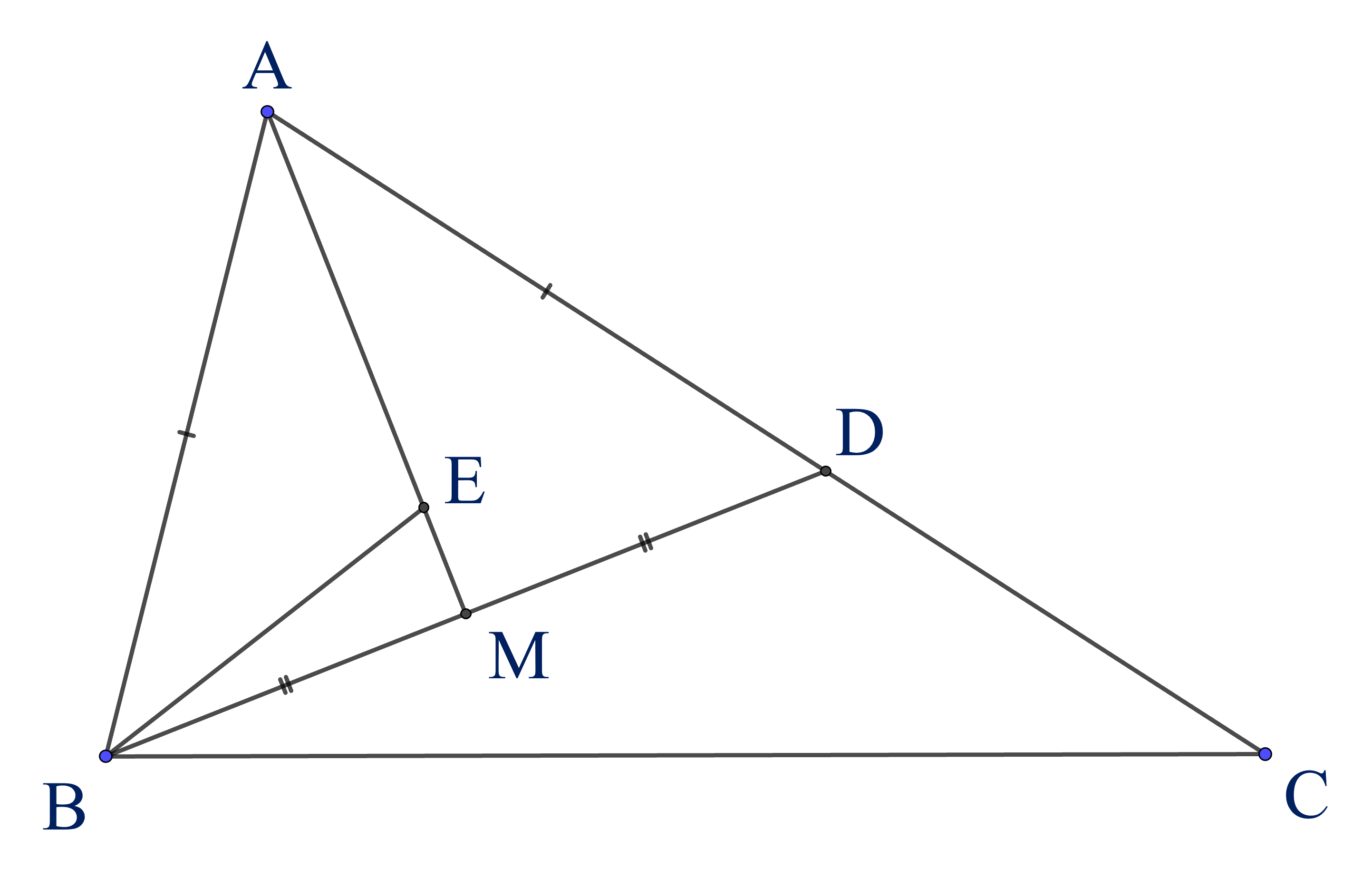
Cho tam giác $ {ABC}$ có $ {AB}< {AC}$. Trên cạnh $ {AC}$ lấy điểm $ {D}$ sao cho $ {AD}= {AB}$. Gọi $ {M}$ là trung điểm của $B D$; $E$ là giao điểm của tia phân giác góc $B$ với tia $A M$.
a)(1,25 điểm) Chứng minh rằng tia $ {AM}$ là tia phân giác góc $ {A}$ của tam giác $ {ABC}$.
b)(0,75 điểm) Cho góc $C$ có số đo bằng $30^{\circ}$. Hãy tính số đo góc $ACE$.
Hướng dẫn giải:
a)(0,5 điểm)
b) (0,75 điểm)
Xét $\triangle A D M$ và $\triangle A B M$ có $A D=A B$ (giả thiết); $D M=B M$ (giả thiết $M$ là trung điểm của $B D$ ); $A M$ chung. Suy ra $\triangle A D M=\triangle A B M$ (c.c.c).
Do đó $\widehat{D A M}=\widehat{B A M}$ (góc tương ứng). Vì vậy $A M$ là tia phân giác góc $A$ của tam giác $A B C$.
c) (0,75 điểm)
Theo chứng minh trên, có $A M$ là tia phân giác góc $A$. Lại có $ {E}$ là giao điểm của tia phân giác góc $ {B}$ với tia $ {AE}$ (giả thiết).
Như vậy $E$ là giao điểm của tia phân giác góc $ {A}$ với tia phân giác góc $ {B}$. Suy ra $CE$ là phân giác góc $C$ (theo định lí: ba đường phân giác của tam giác đồng quy tại một điểm).
Từ đó $\widehat{A C E}=\dfrac{1}{2} \widehat{C}=15^{\circ}$.
(0,5 điểm)
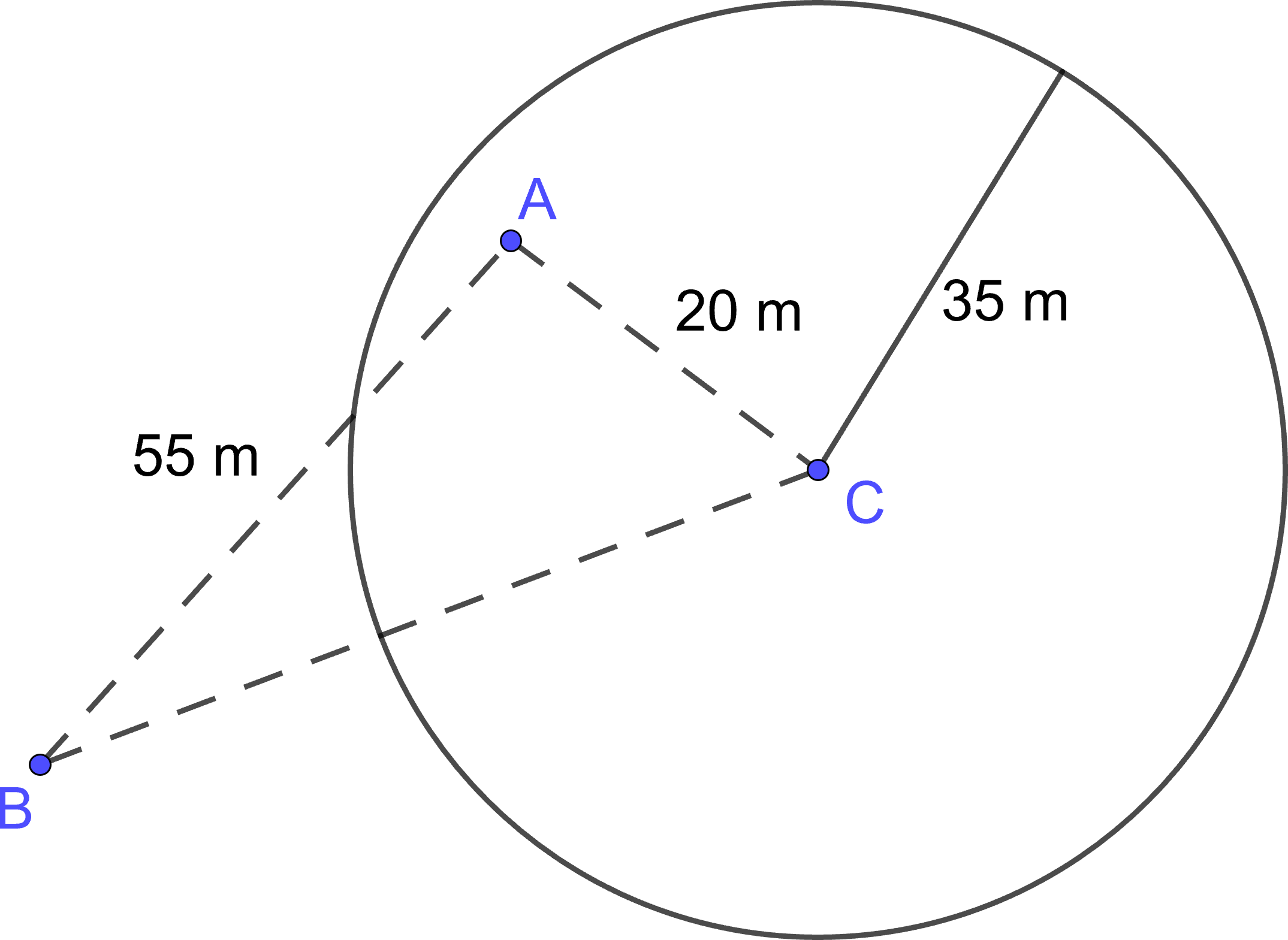
Ông A và ông B đứng cách nhau $55$ mét. Một bộ phát wifi có bán kính hoạt động $35$ mét và cách ông A $20$ mét. Em hãy cho biết điện thoại di động của ông A hay ông B không nhận được sóng wifi? Vì sao?
Hướng dẫn giải:
(Không yêu cầu vẽ hình).
Kí hiệu A, B là vị trí ông A và ông B đang đứng. C là vị trí bộ phát wifi.
Trong $\Delta ABC$ có $BC>AB-AC=55-20=35$.
Suy ra khoảng cách từ ông B đến vị trí bộ phát wifi lớn hơn bán kính hoạt động của bộ phát. Do đó ông B không nhận được sóng wifi.
Khoảng cách từ ông A đến bộ phát wifi là $20$ m(nhỏ hơn bán kính hoạt động của bộ phát) nên ông A nhân được sóng wifi.
