Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tự luận (10 điểm) SVIP
Câu 1. (2,0 điểm) Thực hiện phép tính:
a) $\sqrt{20}+2 \sqrt{45}-3 \sqrt{80}+\sqrt{125}$.
b) $\dfrac{2 \sqrt{3}+3 \sqrt{2}}{\sqrt{3}+\sqrt{2}}-4 \sqrt{\dfrac{3}{2}}-\dfrac{5}{1-\sqrt6}$.
c) $\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4(\sqrt{x}-1)}{x-2 \sqrt{x}}$ với $x \neq 4, x>0$.
Hướng dẫn giải:
a) $\sqrt{20}+2 \sqrt{45}-3 \sqrt{80}+\sqrt{125}$
$=2\sqrt{5}+2. 3\sqrt{5}-3. 4\sqrt{5}+5\sqrt{5}$
$=2\sqrt{5}+6\sqrt{5}-12\sqrt{5}+5\sqrt{5}=\sqrt{5}$.
b) $\dfrac{2 \sqrt{3}+3 \sqrt{2}}{\sqrt{3}+\sqrt{2}}-4 \sqrt{\dfrac{3}{2}}-\dfrac{5}{1-\sqrt{6}}$
$=\dfrac{\sqrt{6}(\sqrt{2}+\sqrt{3})}{\sqrt{3}+\sqrt{2}}-4 . \dfrac{\sqrt{6}}{2}-\dfrac{5 .(1+\sqrt{6})}{1-6}$
$=\sqrt{6}-2 \sqrt{6}+1+\sqrt{6}=1$
c) $\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4(\sqrt{x}-1)}{x-2 \sqrt{x}}$ với $x \neq 4, x>0$.
$=\dfrac{{{(\sqrt{x})}^{2}}-4\sqrt{x}+4}{\sqrt{x}(\sqrt{x}-2)}$
$=\dfrac{{{(\sqrt{x}-2)}^{2}}}{\sqrt{x}(\sqrt{x}-2)}$
${{\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-2)}=\dfrac{(\sqrt{x})^{2}-4 \sqrt{x}+4}{\sqrt{x}(\sqrt{x}-2)}=\dfrac{(\sqrt{x}-2)^{2}}{\sqrt{x}(\sqrt{x}-2)}=\dfrac{\sqrt{x}-2}{\sqrt{x}}}}$
Câu 2. (1,5 điểm) Giải các phương trình sau:
a) $\dfrac{5}{3} \sqrt{9 x+18}+\dfrac{1}{2} \sqrt{4 x+8}-15=\sqrt{2+x}$.
b) $\sqrt{x^{2}-4 x+4}-6=2 x$.
Hướng dẫn giải:
a) $\dfrac{5}{3} \sqrt{9 x+18}+\dfrac{1}{2} \sqrt{4 x+8}-15=\sqrt{2+x}$.
Ta có $\dfrac{5}{3} \sqrt{9 x+18}+\dfrac{1}{2} \sqrt{4 x+8}-15=\sqrt{2+x} $
$\Leftrightarrow \dfrac{5}{3} \sqrt{9(x+2)}+\dfrac{1}{2} \sqrt{4(x+2)}-15=\sqrt{x+2}$
$\Leftrightarrow 5 \sqrt{x+2}+\sqrt{x+2}-\sqrt{x+2}=15$
$\Leftrightarrow \sqrt{x+2}=3\Leftrightarrow x+2=9\Leftrightarrow x=7.$
Vậy tập nghiệm của phương trình là $S=\{7\}$.
b) $\sqrt{x^{2}-4 x+4}-6=2 x$.
${{\sqrt{x^{2}-4 x+4}-6=2 x \Leftrightarrow \sqrt{(x-2)^{2}}=2 x+6 \Leftrightarrow|x-2|=2 x+6}}$
$|x-2|=2x+6\Leftrightarrow \left\{ \begin{aligned} &x\ge -3 \\ &\left[ \begin{aligned} &x-2=2x+6 \\ &x-2=-2x-6 \\ \end{aligned} \right. \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} &x\ge -3 \\& \left[ \begin{aligned} &x=-8\,\,\,\left( l \right) \\ &x=-\dfrac{4}{3}\,\,\left( tm \right) \\ \end{aligned} \right. \\ \end{aligned} \right.\Leftrightarrow x=-\dfrac{4}{3}$.
Vậy tập nghiệm của phương trình $S=\left\{-\dfrac{4}{3}\right\}$.
Câu 2. (2,0 điểm) Cho hàm số $y=\dfrac{1}{2} x+2$ có đồ thị $\left(D_{1}\right)$ và $y=-x+3$ có đồ thị $\left(D_{2}\right)$.
a) Vẽ đồ thị hai hàm số trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm $A$ của đồ thị hai hàm số trên.
c) Viết phương trình đường thẳng $(D): \, y=a x+b$ biết $(D)$ song song với $\left(D_{2}\right)$ và $(D)$ cắt $\left(D_{1}\right)$ tại điểm có hoành độ $x=-2$.
Hướng dẫn giải:
a) Bảng giá trị hàm số $y = \dfrac12x + 2$:
| $x$ | $0$ | $2$ |
| $y = \dfrac12x + 2$ | $2$ | $3$ |
Bảng giá trị hàm số $y = -x + 3$:
| $x$ | $0$ | $1$ |
| $y = -x + 3$ | $3$ | $2$ |
Đồ thị hàm số:

b) Phương trình hoành độ giao điểm của $\left(D_{1}\right)$ và $\left(D_{2}\right)$ là:
$\dfrac{1}{2} x+2=-x+2 \Leftrightarrow x=\dfrac{2}{3}.$
Thế $x=\dfrac{2}{3}$ vào $y=-x+3=-\dfrac{2}{3}+3=\dfrac{7}{3}$.
Vậy tọa đọa giao điểm là $A\left(\dfrac{2}{3} ; \dfrac{7}{3}\right)$.
c) Vì $(D)$ song song với $\left(D_{2}\right)$ nên $a=-1$ và $b \neq 3$.
Do đó $(D): \, y=-x+b$.
Gọi $B\left(x_{B} ; y_{B}\right)$ là giao điểm của $(D)$ và $\left(D_{1}\right)$ tại điểm có hoành độ là $-2$ nên $B\left(-2 ; y_{B}\right)$.
Ta có $B \in\left(D_{1}\right) \Rightarrow y_{B}=\dfrac{1}{2} .(-2)+2=1$.
Vậy $B(-2 ; 1)$.
Ta có $B(-2 ; 1) \in(D): \, y=-x+b \Rightarrow 1=-1 .(-2)+b \Leftrightarrow b=-1$ (tm).
Vậy $(D): \, y=-x-1$.
Câu 4 (0,75 điểm): Nhân dịp 2/9 siêu thị điện máy Nguyễn Kim có khuyến mãi trên hóa đơn tính tiền. Nếu hóa đơn trị giá từ 5 000 000 đồng thì giảm 5%; từ 12 000 000 đồng trở lên thì giảm 12% kèm theo tiền quà tặng 300 000 đồng (còn dưới 12 000 000 đồng sẽ không có quà tặng). Bác Đô đã mua một quạt máy giá 2 200 000 đồng, một máy lạnh giá 12 000 000 đồng, một nồi cơm điện giá 1 500 000 đồng ở siêu thị đó. Bác Đô đã phải trả bao nhiêu tiền khi mua hàng?
Hướng dẫn giải:
Tổng số tiền các món hàng khi chưa giảm là:
2 200 000 + 12 000 000 + 1 500 000 = 15 700 000 (đồng)
Tổng số tiền bác Đô phải trả:
15 700 000.( 1 - 12%) - 300 000 = 13 516 000 (đồng).
Câu 5. (0,75 điểm) Một máy bay cất cánh theo phương có góc nâng $23^\circ$ (so với mặt đất như hình vẽ).
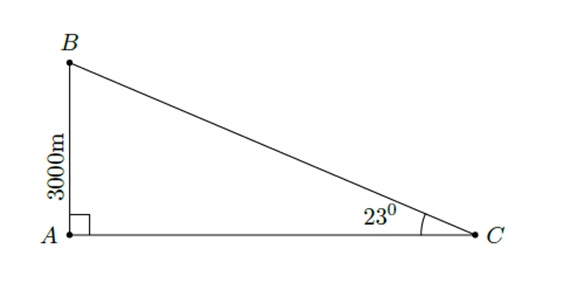
Muốn đạt độ cao $3 \, 000$ m so với mặt đất thì máy bay phải bay một đoạn đường là bao nhiêu mét? (kết quả làm tròn đến hàng đơn vị).
Hướng dẫn giải:
Tam giác $B A C$ vuông tại $A$: $\sin \,C=\dfrac{AB}{BC}{ }$ (tỉ số lượng giác)
$\sin 23^\circ =\dfrac{3 \, 000}{BC}\Rightarrow BC=\dfrac{3 \, 000}{\sin 23^\circ }\approx 7 \, 678$ m.
Vậy máy bay phải bay một đoạn đường $7 \, 678$ m để đạt độ cao $3 \, 000$ m.
Câu 6. (3,0 điểm) Từ một điểm ${{A}}$ nằm ngoài đường tròn ${{(O ; R)}}$, kẻ hai tiếp tuyến ${{AB, A C}}$ với $(O;R)\,\,\,(B$ và ${{C}}$ là hai tiếp điểm).
a) Chứng minh bốn điểm $A, \, B, \, O, \, C$ cùng thuộc một đường tròn và $A O \perp B C$ tại ${{H}}$.
b) Vẽ đường kính ${{B D}}$. Đường thẳng qua ${{O}}$ và vuông góc với ${{A D}}$ cắt tia ${{B C}}$ tại ${{E}}$. Chứng minh $D C$ // $O A$ và ${{C D \cdot C O=A B \cdot C E}}$.
c) Chứng minh ${{D E}}$ là tiếp tuyến của đường tròn ${{(O ; R)}}$.
Hướng dẫn giải:
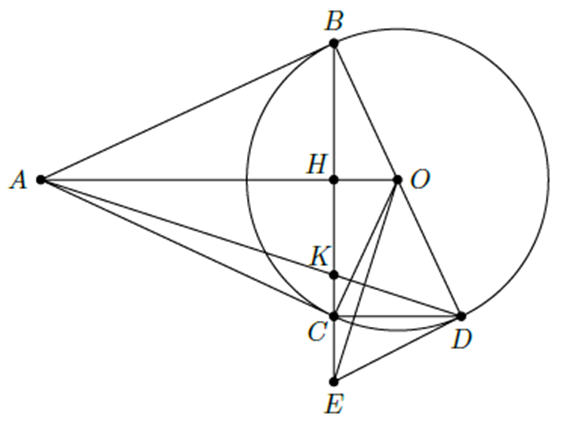
a) Ta có $A B \perp B O$ và $A C \perp C O$ (vì $A B$ và $A C$ lần lượt là các tiếp tuyến của $(O)$).
Vậy $\widehat{A B O}=90^\circ$ và $\widehat{A C O}=90^\circ$.
Xét $\Delta A B O$ vuông tại $B$ và $\Delta A C O$ vuông tại $C$ có cùng cạnh huyền $A O$.
Suy ra $\Delta A B O$ và $\Delta A C O$ nội tiếp đường tròn có đường kính $A O$.
Vậy $A, \, B, \, O, \, C$ cùng thuộc một đường tròn.
Ta có $A B=A C$ (tính chất hai tiếp tuyến $AB$, $AC$ cắt nhau) $\Rightarrow A$ cách đều $B$, $C$
$O B=O C=R_{(O)}\Rightarrow O$ cách đều $B$, $C$.
Vậy $A O$ là trung trực của $B C$ nên $A O \perp B C$ tại $H$ và $H$ là trung điểm $B C$.
b) Xét $\Delta B C D$ nội tiếp $(O)$ có $B D$ là đường kính suy ra $\Delta B C D$ vuông tại $C$.
Vậy $C D \perp B C$.
Ta có $C D \perp B C$ (chứng minh trên).
$A O \perp B C$ (chứng minh trên).
Vậy $C D$ // $A O$ (từ vuông góc đến song song).
Gọi $K$ là giao điểm của $A D$ và $B C$.
Ta có $\widehat{A C B}=\widehat{O C D}$ (cùng phụ $\widehat{B C O}$).
Ta có $\widehat{A C D}=\widehat{A C B}+\widehat{B C D}=90^\circ+\widehat{A C B}$.
$\widehat{O C E}=\widehat{O C D}+\widehat{C D E}=90^\circ+\widehat{O C D}$.
Vậy $\widehat{A C D}=\widehat{O C E}$.
Xét $\Delta A C D$ và $\Delta D C E$ có $\widehat{A C D}=\widehat{O C E}$ (chứng minh trên).
$\widehat{C D A}=\widehat{C E O}$ (cùng phụ $\widehat{D K E}$).
Vậy $\Delta A C D \backsim \Delta O C E$ (góc - góc).
Vậy $\dfrac{A C}{C O}=\dfrac{C D}{C E} \Leftrightarrow A C \cdot C E=C O \cdot C D$ mà $A B=A C$ do tính chất hai tiếp tuyến bằng nhau nên ta có $A B \cdot C E=C O \cdot C D$.
c) Xét $\Delta B C D$ vuông tại $C$ và $\Delta A C O$ vuông tại $O$ ta có
$\widehat{A O C}=\widehat{O C D}=\widehat{B D C}$.
Vậy $\Delta A C O \backsim \Delta B C D$ (góc - góc).
Suy ra $\dfrac{A C}{B C}=\dfrac{C O}{C D} \Leftrightarrow \dfrac{A C}{C O}=\dfrac{B C}{C D}$
Ta có $\dfrac{A B}{C O}=\dfrac{B C}{C D}\left(\dfrac{A C}{C O}=\dfrac{B C}{C D}\right)$.
$\dfrac{A B}{C O}=\dfrac{C D}{C E}$ (chứng minh trên).
Vậy $\dfrac{C D}{C E}=\dfrac{B C}{C D} \Leftrightarrow \dfrac{C D}{B C}=\dfrac{C E}{C D}$.
Xét $\Delta C D E$ vuông tại $C$ và $\Delta C B D$ vuông tại $C$ có $\dfrac{C D}{B C}=\dfrac{C E}{C D}$ nên $\Delta C D E \backsim \Delta C B D$.
Suy ra $\widehat{C D E}=\widehat{D B C}$ nên $\widehat{C D E}+\widehat{C D B}=90^\circ$.
Vậy $B D \perp D E$ nên $D E$ đồng thời là tiếp tuyến của $(O)$ tại $D$.
