Trường hợp bằng nhau: cạnh - cạnh - cạnh (Phần 2) SVIP

Sắp xếp các sau một cách hợp lý để được lời giải bài toán trên.

• AB = AC (giả thiết)
  BM = CM (do M là trung điểm BC)
  AM chung
• ⇒ $\widehat{\text{AMB}}=\widehat{\text{AMC}}$ (hai góc tương ứng) ⇒ $\widehat{\text{AMB}}=\widehat{\text{AMC}}=90^o$ (Do hai góc kề bù với nhau) ⇒AM $\perp$ BC.
• Xét ΔABM và ΔACM ta có:
• Suy ra ΔABM = ΔACM (c - c - c)

Cho bốn điểm $A$, $B$, $C$, $D$ thuộc đường tròn $(O)$ sao cho $BD = CA$.

$\widehat{{BOD}}$ bằng góc nào sau đây?

Cho tam giác BDA có AB = AD và tam giác BDC có CB = CD (A và C nằm khác phía đối với BD).

Khẳng định nào dưới đây luôn đúng?

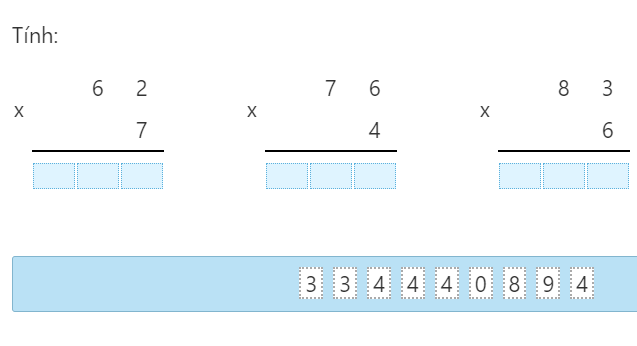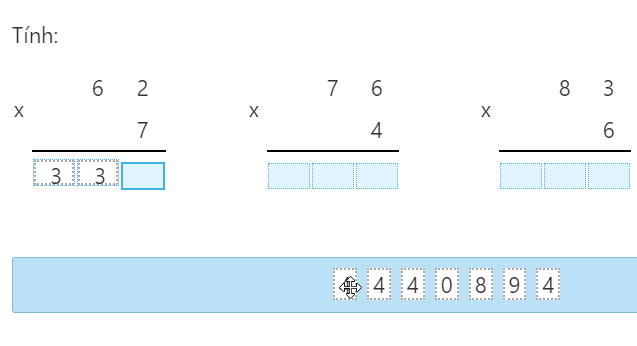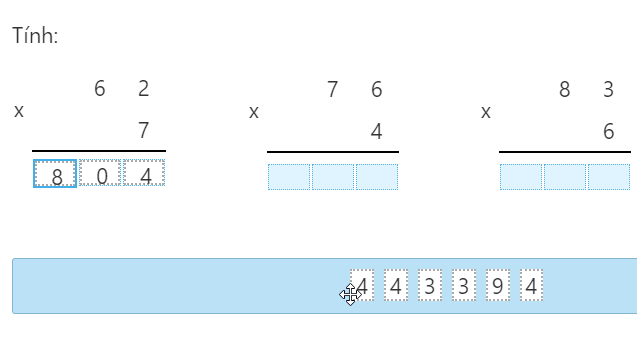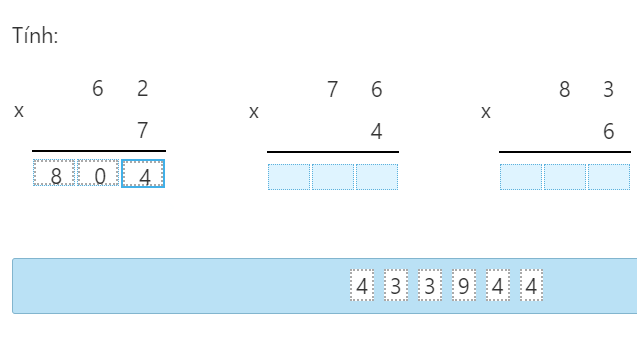
Cho đoạn thẳng AB. Vẽ cung tròn tâm A và cung tròn tâm B bán kính BA, chúng cắt nhau ở D và C.

Điền kí hiệu thích hợp vào ô trống

ΔABD = ;

ΔADC = .

Cho bài toán:

Cho tam giác DBA. Vẽ cung tròn tâm D bán kính BA, vẽ cung tròn tâm A bán kính BD, chúng cắt nhau ở C (C và B nằm khác phía đối với DA). Chứng minh rằng DC // BA.

Chọn kí hiệu thích hợp điền vào ô trống để được lời giải bài toán trên.