Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Trắc nghiệm ôn tập hình học SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho xOy=45∘. Trên cùng một nửa mặt phẳng bờ là tia Ox chứa tia Oy vẽ tia Oz sao cho yOz=90∘, Ot là tia đối của tia Ox.
Khẳng định nào sau đây sai?
Tia Ot là tia phân giác của góc xOy khi
Quan sát hình vẽ và hoàn thành các khẳng định.
![]() A1=A3 (hai góc
A1=A3 (hai góc
- kề bù
- so le trong
- đối đỉnh
- đồng vị
![]() B1+B2=180∘ (hai góc
B1+B2=180∘ (hai góc
- đối đỉnh
- kề bù
- đồng vị
- so le trong
![]() B3 và A1 là hai góc
B3 và A1 là hai góc
- so le trong
- đối đỉnh
- đồng vị
Cho hình vẽ:
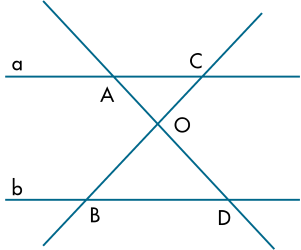
Biết đường thẳng a song song với đường thẳng b. Những cặp góc bằng nhau của hai tam giác OAC và ODB là
Cho hình vẽ:
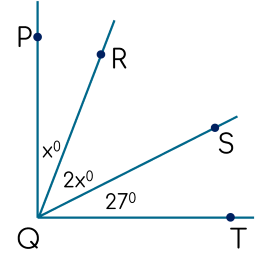
Biết PQT=90∘, số đo RQS và RQP lần lượt bằng
Cho hai tam giác:
Điền vào ô trống: Δ=ΔBAD.
(Chú ý: viết đúng thứ tự các đỉnh tương ứng).
Cho tam giác ADC có CA=CD và tam giác ADB có BA=BD (C và B nằm khác phía đối với AD).
Khẳng định nào sau đây đúng?
Cho ba tam giác với các cạnh và các góc được kí hiệu trên hình vẽ. Chọn cặp tam giác bằng nhau theo trường hợp cạnh - góc - cạnh trong ba tam giác đó.
Cho tam giác ABC có AB<AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. Kẻ IH vuông góc với đường thẳng AB, kẻ IK vuông góc với đường thẳng AC. Chứng minh BH=CK.
Sắp xếp các dòng sau theo thứ tự hợp lí để được lời giải bài toán trên.
- ΔBMI=ΔCMI (c.g.c) ⇒IB=IC. (1)
- ΔAHI=ΔAKI (cạnh huyền - góc nhọn) ⇒IH=IK. (2)
- Từ (1) và (2) suy ra ΔIHB=ΔIKC ⇒BH=CK.
- Gọi M là trung điểm của BC.
Tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD=AE.
Điền kí hiệu thích hợp vào các ô sau:
ABD= .
BDC= .
ECB= .
(Kéo thả hoặc click vào để điền)
Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Ba điểm A, D, E vì chúng cùng nằm trên đường trung trực của đoạn thẳng .
(Kéo thả hoặc click vào để điền)
Vẽ đường thẳng a song song với đường thẳng b, đường thẳng c vuông góc với đường thẳng b.
Khi đó, đường thẳng c
- song song
- vuông góc
Cho tam giác ABC. Các tia phân giác các góc B và C cắt nhau ở O. Kẻ OD ⊥ AC, kẻ OE ⊥ AB. Chứng minh rằng OD=OE.
Sắp xếp các dòng sau theo thứ tự hợp lý để được lời giải bài toán trên.
- ΔOHB=ΔOEB (cạnh huyền - góc nhọn) ⇒OH=OE (cạnh tương ứng) (1)
- Kẻ OH ⊥ BC.
- Từ (1) và (2) suy ra OD=OE (cùng bằng OH).
- ΔOHC=ΔODC (cạnh huyền - góc nhọn) ⇒OH=OD (cạnh tương ứng) (2)
Những hình nào sau đây có hai góc xAy và xAz kề nhau?
Khẳng định nào dưới đây đúng?
