Bài học cùng chủ đề
- Tỉ số lượng giác của góc nhọn
- Khái niệm tỉ số lượng giác của một góc nhọn
- Tỉ số lượng giác của một góc nhọn đặc biệt
- Tỉ số lượng giác của hai góc phụ nhau
- Tỉ số lượng giác của góc nhọn
- Tỉ số lượng giác của các góc nhọn đặc biệt
- Tỉ số lượng giác của các góc phụ nhau
- Bài toán thực tế ứng dụng tỉ số lượng giác của góc nhọn
- Phiếu bài tập tuần 3. Tỉ số lượng giác của góc nhọn
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tỉ số lượng giác của góc nhọn SVIP
1. Tỉ số lượng giác của một góc nhọn
a. Khái niệm
Cho góc nhọn $\alpha$. Xét tam giác $ABC$ vuông tại $A$ có $\widehat{B} = \alpha$.
⚡Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc $\alpha$, kí hiệu $\sin \alpha$.
$\sin \alpha$ = cạnh đối : cạnh huyền
⚡Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc $\alpha$, kí hiệu $\cos \alpha$.
$\cos \alpha$ = cạnh kề : cạnh huyền
⚡Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc $\alpha$, kí hiệu $\tan \alpha$.
$\tan \alpha$ = cạnh đối : cạnh kề
⚡Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc $\alpha$, kí hiệu $\cot \alpha$.
$\cot \alpha$ = cạnh kề : cạnh đối
Ví dụ 1. Tính các tỉ số lượng giác của góc $B$ trong tam giác $ABC$.
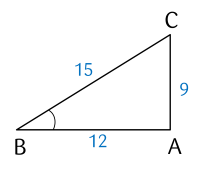
Lời giải
Xét tam giác $ABC$ có $\widehat{A} = 90^\circ$ và $B$ là góc nhọn.
$\sin B = \dfrac{AC}{BC} = \dfrac9{15} = 0,6$;
$\cos B = \dfrac{AB}{BC} = \dfrac{12}{15} = 0,8$;
$\tan B = \dfrac{AC}{AB} = \dfrac9{12} = 0,75$;
$\cot B = \dfrac{AB}{AC} = \dfrac43$.
b. Lưu ý
+ Khi không sợ nhầm lẫn, ta có thể viết $\sin B$, $\cos B$, $\tan B$, $\cot B$ lần lượt thay cho các kí hiệu $\sin \widehat{B}$, $\cos \widehat{B}$, $\tan \widehat{B}$, $\cot \widehat{B}$.
+ Các tỉ số lượng giác của góc nhọn $a$ luôn dương, $\sin a < 1$; $\cos a < 1$ và $\cot a = \dfrac1{\tan a}$.
c) Tỉ số lượng giác của góc nhọn đặc biệt
| $\alpha$ | $\sin \alpha$ | $\cos \alpha$ | $\tan \alpha$ | $\cot \alpha$ |
| $30^\circ$ | $\dfrac12$ | $\dfrac{\sqrt3}2$ | $\dfrac{\sqrt3}3$ | $\sqrt3$ |
| $45^\circ$ | $\dfrac{\sqrt2}2$ | $\dfrac{\sqrt2}2$ | $1$ | $1$ |
| $60^\circ$ | $\dfrac{\sqrt3}2$ | $\dfrac12$ | $\sqrt3$ | $\dfrac{\sqrt3}3$ |
Ví dụ 2. Tính giá trị của biểu thức $P = \dfrac{\sin 30^\circ . \cos 60^\circ}{\tan 45^\circ}$.
Lời giải
$P = \dfrac{\sin 30^\circ . \cos 60^\circ}{\tan 45^\circ} = \dfrac{\dfrac12 . \dfrac12}1 = \dfrac14.$
2. Tỉ số lượng giác của hai góc phụ nhau
Định lí
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Với $0^\circ < a < 90^\circ$ ta có:
⚡$\sin (90^\circ - a) = \cos a$; ⚡$\cos (90^\circ - a) = \sin a$;
⚡$\tan (90^\circ - a) = \cot a$; ⚡$\cot (90^\circ - a) = \tan a$;
Ví dụ 3. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn $45^\circ$.
a) $\sin 60^\circ$;
b) $\cot 82^\circ$.
Lời giải
a) $\sin 60^\circ = \cos 30^\circ$;
b) $\cot 82^\circ = \tan 8^\circ$.
Bạn có thể đăng câu hỏi về bài học này ở đây
