Tập hợp SVIP

1. CÁC KHÁI NIỆM CƠ BẢN VỀ TẬP HỢP

a. Tập hợp

Có thể mô tả một tập hợp bằng một trong hai cách sau:

Cách 1. Liệt kê các phần tử của tập hợp;

Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

 Chú ý. Số phần tử của tập hợp \(S\) kí hiệu là \(n\left(S\right)\).

• \(a\in S\): phần tử \(a\) thuộc tập hợp \(S\).
• \(a\notin S\): phần tử \(a\) không thuộc tập hợp \(S\).

Tập hợp không chứa phần tử nào được gọi là tập rỗng, kí hiệu là \(\varnothing\).

Ví dụ. Cho tập hợp \(A=\left\{x\inℕ|2< x< 7\right\}\).

a) Viết tập hợp \(A\) bằng cách liệt kê các phần tử. Tập hợp \(A\) có bao nhiêu phần tử?

b) Trong các số 1; 5; 8 số nào thuộc \(A\), số nào không thuộc \(A\)?

Giải

a) \(A=\left\{3;4;5;6\right\}\). \(n\left(A\right)=4\).

b) \(1\notin A;5\in A;8\notin A\).

b. Tập hợp con 

Nếu mọi phần tử của tập hợp \(T\) đều là phần tử của tập hợp \(S\) thì ta nói \(T\) là một tập hợp con (tập con) của \(S\) và viết là \(T\subset S\) (đọc là \(T\) chứa trong \(S\) hoặc  \(T\) là tập con của \(S\)).

Thay cho viết \(T\subset S\), ta còn viết \(S\supset T\) (đọc là \(S\) chứa \(T\)).

Kí hiệu \(T\)\(\not\subset \)\(S\) để chỉ \(T\) không là tập con của \(S\).

Nhận xét.

+ Từ định nghĩa trên, $T$ là tập con của $S$ nếu mệnh đề sau đúng: $\forall x \in T \Rightarrow x \in S$.

+ Quy ước tập rỗng là tập con của mọi tập hợp.

Người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven.

 Ví dụ. Minh họa tập hợp T.

c. Hai tập hợp bằng nhau

Hai tập hợp \(S\) và \(T\) được gọi là hai tập hợp bằng nhau nếu mỗi phần tử của \(T\) cũng là phần tử của tập hợp \(S\) và ngược lại. Kí hiệu là \(S=T\).

2. CÁC TẬP HỢP SỐ

a. Mối quan hệ giữa các tập hợp số

 Mối quan hệ giữa các tập hợp số: \(ℕ\subsetℤ\subsetℚ\subsetℝ\).

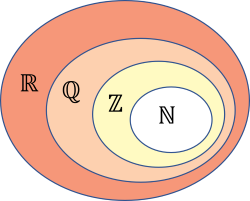
b. Các tập con thường dùng của \(ℝ\)

Một số tập con thường dùng của \(ℝ\):

• Khoảng

\(\left(a;b\right)=\left\{x\inℝ|a< x< b\right\}\)
\(\left(a;+\infty\right)=\left\{x\inℝ|x>a\right\}\)
\(\left(-\infty;b\right)=\left\{x\inℝ|x< b\right\}\)
$(-\infty;+\infty)$

• Đoạn

\(\left[a;b\right]=\left\{x\inℝ|a\le x\le b\right\}\)

• Nửa khoảng

\([a;b)=\left\{x\inℝ|a\le x< b\right\}\)
\((a;b]=\left\{x\inℝ|a< x\le b\right\}\)
\([a;+\infty)=\left\{x\inℝ|x\ge a\right\}\)
\((-\infty;b]=\left\{x\inℝ|x\le b\right\}\)

 Chú ý.

• Kí hiệu \(+\infty\): Đọc là dương vô cực (hoặc dương vô cùng).
• Kí hiệu \(-\infty\): Đọc là âm vô cực (hoặc âm vô cùng).
• $a, b$ được gọi là các đầu mút của khoảng, đoạn, nửa khoảng.