Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Số gần đúng SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Qua bài học này, các em sẽ nắm được:
- Thế nào là số gần đúng, số đúng.
- Một số ví dụ thường gặp của số đúng.
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Cho bảng kết quả đo chiều dài của cái bảng (không tính khung bảng) của năm bạn.
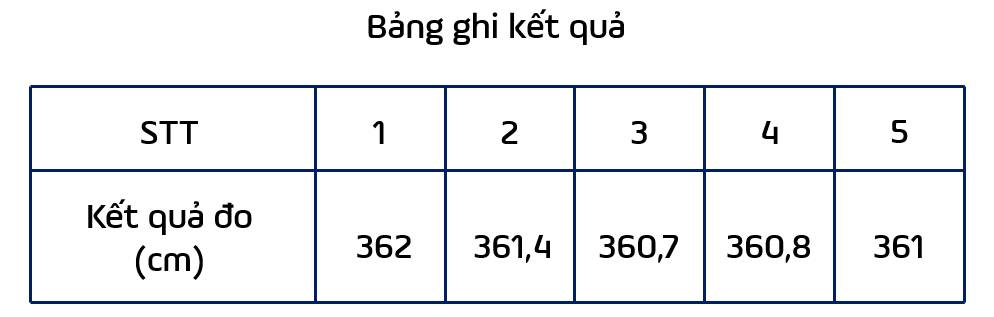
Biết thông số mà nhà sản xuất đưa ra cho chiều dài bảng (không tính khung bảng) là 360 cm, kết quả đo nào gần với thông số này nhất?
362 cm.
361,4 cm.
361 cm.
360,7 cm.
360,8 cm.
Câu 2 (1đ):
Cho tam giác vuông cân có độ dài cạnh góc vuông là 1 cm. Để biết số đo cạnh huyền, có cách làm như sau:
- Sử dụng thước kẻ (vạch chia mm) đo được chiều dài cạnh huyền là 1,4 cm.
- Sử dụng định lí Py - ta - go, tính được chiều dài cạnh huyền là 2 cm.
| Vậy, | số gần đúng là , |
| số đúng là . |
1,42
(Kéo thả hoặc click vào để điền)
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Chào mừng các em đã quay trở lại với
- khóa học toán trực tuyến trên trang web
- online.vn
- trong Bài học này chúng ta sẽ cùng nhau
- đến với bài đầu tiên của chương 5 các số
- đặc trưng của mẫu số liệu không ghép
- nhóm bài 12 số gần đúng và sai số
- chúng ta đến với phần đầu tiên số gần
- đúng
- trước khi vào nội dung chính của phần
- này thì chúng ta đến với tình huống Xem
- Tại sao lại cần phải có khái niệm số gần
- đúng
- tình huống của chúng ta đo chiều dài của
- cái bảng viết phấn
- năm bạn học sinh trong lớp được yêu cầu
- sử dụng thước kẻ học sinh
- để đo chiều dài bảng viết phấn kết quả
- thu được được ghi lại vào bảng dưới đây
- bạn thứ nhất đo được chiều dài của cái
- bảng là 362 cm
- bạn thứ hai đo được là 361,4 Cm
- bạn thứ ba đo được là 360,7 Cm
- đoạn thứ tư đo được là 360,8 cm
- và bạn cuối cùng đo được là 361 cm
- nhìn vào bảng ghi kết quả này thì chúng
- ta thấy xảy ra một hiện tượng đó là cùng
- một chiều dài của cái bảng thì 5 bạn đo
- ra 5 chiều dài khác nhau
- các em hoàn toàn có thể kiểm chứng lại
- tình huống này bằng cách dù các bạn ở
- trong lớp đo chiều dài của cái bảng để
- xem liệu chúng ta có ra cùng một kết quả
- hay không Hay là chúng ta sẽ ra các kết
- quả gần giống nhau như thế này
- bây giờ thầy sẽ nêu ra một số nguyên
- nhân vì sao chúng ta đo cùng một cái
- bảng mà lại ra nhiều kết quả đo như vậy
- cụ thể khi chúng ta đo chiều dài của cái
- bảng không tính mép bảng chúng ta sẽ đặt
- thước
- vuông góc với mép bảng đứng ở dọc chúng
- ta
- và đến đây chúng ta sẽ đánh dấu điểm
- cuối cùng của thước
- tiếp theo là chúng ta sẽ dịch thước và
- lại đánh dấu đến điểm tiếp theo
- cứ làm như vậy là chúng ta có thể đo
- được chiều dài của cái bảng bằng cách
- cộng chiều dài các thước và đoạn còn lại
- này
- tuy nhiên vấn đề đặt ra của chúng ta là
- để đo chính xác thì ta cần phải đặt
- thước vuông góc một cách hoàn hảo với
- mép của bạn
- tuy nhiên thì liệu đôi tay của chúng ta
- có hoàn hảo để được như vậy không Hay là
- khi đặt thước chúng ta sẽ bị xiên lệch
- đi một vài độ
- và đến đây chúng ta sẽ đánh dấu
- rồi lại làm Bước tiếp theo
- bước tiếp theo liệu chúng ta có thể đặt
- thước vuông góc được với mép bảng hay
- không Hay là lại lệch đi một vài độ
- và chúng ta có thể hiểu được là mỗi lần
- đo chúng ta sẽ bị lệch đi từng chút từng
- chút một
- và như vậy thì sau mỗi lần đo kết quả
- chúng ta thu được khác nhau cũng là điều
- tất yếu
- ở tình huống này thì các em có thể kiểm
- chứng để thấy được sự xuất hiện của một
- số gần đúng cụ thể hơn khi chúng ta đo
- bất kỳ một đồ vật nào thì thường kết quả
- chúng ta thu được sẽ là số phần đúng
- Thầy có kết luận sau đây Trong các tình
- huống đo lường số liệu mà ta thu được
- thường là số gần đúng
- Thầy có thể lấy ví dụ cho các em một số
- tình huống đo lường thường gặp mà chúng
- ta sẽ gặp số gần đúng
- tình huống đầu tiên đó là khi chúng ta
- cần cắt vật phẩm
- số liệu mà chúng ta thu được về cân nặng
- của vật phẩm khi nhìn ở đồng hồ cân cũng
- thường là số gần đúng Thầy có thể lấy ví
- dụ về cân nặng của một gói mì chính 450g
- nhìn trên cân thì các em có thể thấy cân
- chỉ đúng là 450g Tuy nhiên
- có thể sẽ có một vài sai số lệch lạc nhỏ
- cái cân mà mắt thường của chúng ta không
- có thể nhìn thấy được ta có thể kiểm
- chứng bằng cách cho 10 gói mì chính 450g
- Hay là cho 20 gói mì chính 450g để xem
- tổng số hơn có được như ban đầu Hay
- không Hay là sẽ bị lệch đó là tầm nửa
- lạng hoặc là một lạng
- tình huống này thì sẽ phù hợp hơn với
- các bạn có gia đình bán tạp hóa
- là tình huống chúng ta gặp ở trong
- trường trung học cơ sở đó là tình huống
- đo chiều cao của cột cờ hay ở đo chiều
- cao của cây cối
- việc chúng ta đo chiều cao ở cột cờ hay
- cây cối sẽ có bước là chúng ta phải
- đến bước chân đi từ cột cờ cho đến ống
- ngắm
- Và khi chúng ta đến mức Chân Như vậy sẽ
- rất dễ xảy ra sai lệch và như vậy chiều
- cao của cột cờ tính được theo tỉ số của
- tam giác đồng dạng sẽ là số gần đúng
- và cuối cùng tình huống đo lường của
- chúng ta đó là đo diện tích của ngôi nhà
- thông thường nếu như tự do thì chúng ta
- sẽ đếm các ô gạch mà được Lát Và tất
- nhiên khi đến các ô gạch thì người ta
- thường sẽ bỏ qua các rãnh ở giữa hai
- viên gạch do đó
- diện tích của ngôi nhà chúng ta tính
- được cũng chỉ là số gần đúng bây giờ
- chúng ta sẽ đến với một số ký hiệu mà
- chúng ta cần phải nhớ khi học phần này
- đó là số đúng được kí hiệu chung là a
- ngang như thế này
- tiếp theo là số gần đúng ký hiệu là A
- số đúng là một số rất khó xác định còn
- số gần đúng là số ta thu được qua quá
- trình đo lường
- bây giờ chúng ta sẽ sang một ví dụ để
- phân biệt số đúng và số gần đúng
- Thầy có ví dụ về độ dài của cạnh huyền
- của một tam giác vuông cân
- để biết được độ dài cạnh huyền của một
- tam giác vuông cân thì chúng ta có 2
- cách làm như sau cách đầu tiên đó là
- chúng ta sẽ vẽ tam giác vuông cân với độ
- dài cạnh bằng 1 và rồi dùng thước kẻ đo
- ta được độ dài của cạnh huyền là 1,4 cm
- cách số 2 là chúng ta sử dụng định lý
- Pitago để chúng ta tính độ dài của cạnh
- huyền sẽ là căn 2 cm
- theo các em ở trong hai trường hợp này
- đâu là số đúng và đâu là số gần đúng
- Chúng ta thấy ngay 1,4 cm là số gần đúng
- còn Căn 2 là số đúng
- Tuy nhiên thì khi chúng ta viết căn bậc
- hai số học của 2 như thế này là chẳng
- qua cũng là ký hiệu mà thôi Và liệu thì
- có phương pháp nào để chúng ta tìm tất
- cả những số thập phân của căn 2 hay
- không
- để trả lời câu hỏi này thầy sẽ để ở dưới
- phần tham khảo ngay sau đây
- đến đây là các em đã có đủ các kiến thức
- để chúng ta học đến bài tiếp theo
- Tuy nhiên thì thầy vẫn muốn giới thiệu
- ứng dụng của số gần đúng qua một vật
- phẩm rất là gần gũi với chúng ta
- đó là chiếc máy tính Casio
- như chúng ta đã biết số căn 2 là một số
- vô tỉ số căn 2 xuất hiện khi chúng ta vẽ
- tam giác vuông cân có độ dài hai cạnh
- góc vuông bằng 1 như vậy cạnh huyền sẽ
- có độ lớn là √2
- khi chúng ta sử dụng thước kẻ chúng ta
- vẽ tam giác này và khi chúng ta đo cạnh
- huyền thì chắc chắn cách chia đoạn thẳng
- đến từng mm của thước kẻ không thể đo
- chính xác được số căn 2 bằng bao nhiêu
- như vậy làm như thế nào để chúng ta có
- thể tìm được các chữ số thập phân của
- căn 2
- như chúng ta đã biết do một nhỏ hơn 2
- nhỏ hơn 4 Và bây giờ chúng ta sẽ lấy căn
- của 3 vế thì ta sẽ suy ra được 1 sẽ nhỏ
- hơn căn 2 nhỏ hơn 2 điều này có nghĩa là
- chúng ta sẽ tìm các số thập phân
- sao cho số thập phân đó nằm ở giữa 1 và
- 2 Tuy nhiên khi bình phương lên phải
- không được vượt quá 2 bây giờ chúng ta
- sẽ cùng nhau tìm các chữ số thập phân
- của √2 tất nhiên việc chúng ta tìm như
- thế này ta hoàn toàn có thể tính được
- tay mà thôi chúng ta sẽ sử dụng máy tính
- cho nhanh
- do một nhỏ hơn căn 2 nhỏ hơn 2 nên chúng
- ta sẽ bắt đầu thử Từ 1,5
- 1,5 bình phương lên
- chúng ta thấy 1,5 Bình Phương đã lớn hơn
- 2 rồi
- Thế nên chúng ta sẽ giảm xuống thành
- 1,4,4 là 1,96
- chúng ta sẽ bắt đầu thử thử 1,41
- đây là một phẩy 9881 cũng chưa vượt quá
- 2
- ta tăng lên
- đây ta thấy 1,42 bình phương đã vượt quá
- 2 nên chúng ta lại giảm xuống lấy số 1
- số gần nhất mà chúng ta chọn
- tiếp theo là chúng ta lấy số 5
- số 5 đã vượt quá 2 rồi nên chúng ta lại
- giảm xuống
- đây ta được số gần với 2 như thế này ta
- lấy số 4
- và chúng ta cứ làm như vậy là ta có thể
- tìm được tất cả các chữ số thập phân của
- √2 tuy nhiên √2 là số vô tỉ nên
- các bước làm như thế này chúng ta sẽ làm
- đến mãi mãi
- tuy nhiên vì việc làm mãi mãi như vậy
- thì chúng ta cũng cảm thấy được Đây là
- giới hạn của máy tính
- bây giờ chúng ta sẽ ấn số căn 2
- chúng ta sẽ ghi lại số thập phân này vào
- trong tờ giấy
- Bây giờ chúng ta sẽ ghi lại
- chúng ta thấy chưa chạm đến hai chúng ta
- sẽ thêm một số nữa qua số 4 ở đây đến 2
- rồi
- số 5 cũng vẫn là 2
- tao có thể thấy được máy tính ở đây đã
- bắt đầu sử dụng số gần đúng để biểu diễn
- số căn 2
- như vậy Ở đây chỉ cần là số 5 thôi
- tiếp đến là chữ số 6 chữ số 6 là cũng
- không được
- số 5 không được
- số 4 là được
- thì chúng ta có thể thấy là khi chúng ta
- thử bất kỳ một số nào
- thì tạo đều thấy bình phương lên bằng 2
- qua đây chúng ta có thể thấy được đối
- các số vô tỉ mà chúng ta tính ở trên máy
- tính thì thường đã được làm tròn
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022
