Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phép cộng, phép trừ đa thức một biến SVIP
I. CỘNG HAI ĐA THỨC MỘT BIẾN
Nhận xét. Để cộng hai đa thức một biến (theo cột dọc) ta làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột;
- Cộng hai đơn thức trong từng cột, ta có tổng cần tìm.
Chú ý. Khi cộng đa thức theo cột dọc, nếu một đa thức khuyết số mũ nào của biến thì khi viết đa thức đó, ta bỏ trống cột tương ứng với số mũ trên.
Ví dụ: Cho hai đa thức \(=x^4-2x^3+3x^2-5x+1\) và \(B=x^4-2x^2+3x-2\). Tìm tổng \(A+B\).
Giải
Ta có
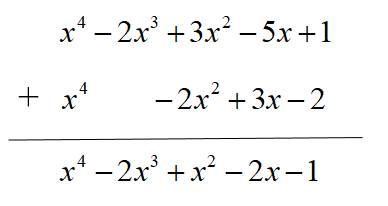
Vậy \(A+B=x^4-2x^3+x^2-2x-1.\)
Nhận xét. Để cộng hai đa thức một biến (theo hàng ngang), ta làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết tổng hai đa thức theo hàng ngang;
- Nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
Ví dụ: Cho hai đa thức \(A=x^4-2x^3+3x^2-5x+1\) và \(B=x^4-2x^2+3x-2\). Tìm tổng \(A+B\).
Giải
\(A+B=\left(x^4-2x^3+3x^2-5x+1\right)+\left(x^4-2x^2+3x-2\right)\)
\(=x^4-2x^3+3x^2-5x+1+x^4-2x^2+3x-2\)
\(=\left(x^4+x^4\right)-2x^3+\left(3x^2-2x^2\right)-\left(5x-3x\right)+\left(1-2\right)\)
\(=2x^4-2x^3+x^2-2x-1\).
II. TRỪ HAI ĐA THỨC MỘT BIẾN
Nhận xét. Để trừ đa thức \(P\left(x\right)\) cho đa thức \(Q\left(x\right)\) (theo cột dọc) ta làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức của \(P\left(x\right)\) ở trên, đơn thức của \(Q\left(x\right)\) ở dưới;
- Trừ hai đơn thức trong từng cột ta được hiệu cần tìm.
Ví dụ: Cho hai đa thức \(A=x^4-2x^3+3x^2-5x+1\) và \(B=x^4-2x^2+3x-2\). Tìm hiệu \(A-B\).
Giải
\(A-B=\left(x^4-2x^3+3x^2-5x+1\right)-\left(x^4-2x^2+3x-2\right)\)
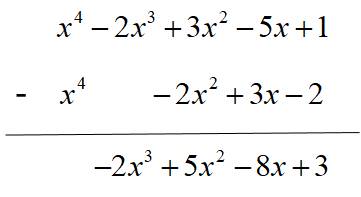
Vậy \(A-B=-2x^3+5x^2-8x+3.\)
Nhận xét. Để trừ đa thức \(P\left(x\right)\) cho đa thức \(Q\left(x\right)\) (theo hàng ngang) ta làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết hiệu \(P\left(x\right)-Q\left(x\right)\) theo hàng ngang, trong đó đa thức \(Q\left(x\right)\) được đặt trong dấu ngoặc;
- Bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức \(Q\left(x\right)\), nhóm các đơn thức có cùng số mũ của biến với nhau.
- Tính hiệu \(P(x)-Q(x)\) bằng cách thực hiện phép tính trong từng nhóm.
Ví dụ: Cho hai đa thức \(A=x^4-2x^3+3x^2-5x+1\) và \(B=x^4-2x^2+3x-2\). Tìm hiệu \(A-B\).
Giải
\(A-B=\left(x^4-2x^3+3x^2-5x+1\right)-\left(x^4-2x^2+3x-2\right)\)
\(A-B=x^4-2x^3+3x^2-5x+1-\left(x^4-2x^2+3x-2\right)\)
\(=x^4-2x^3+3x^2-5x+1-x^4+2x^2-3x+2\)
\(=\left(x^4-x^4\right)-2x^3+\left(3x^2+2x^2\right)-\left(5x+3x\right)+\left(1+2\right)\)
\(=-2x^3+5x^2-8x+3\).
Bạn có thể đăng câu hỏi về bài học này ở đây
