Phép chia đa thức một biến SVIP

1. LÀM QUEN VỚI PHÉP CHIA ĐA THỨC

a. Phép chia hết

Cho hai đa thức \(A\) và \(B\) với \(B\ne0\). Nếu có một đa thức \(Q\) sao cho \(A=B.Q\) thì ta có phép chia hết:

\(A:B=Q\) hay \(\dfrac{A}{B}=Q\), trong đó:

\(A\) là đa thức bị chia; \(B\) là đa thức chia; \(Q\) là đa thức thương (gọi tắt là thương).

Khi đó ta nói đa thức \(A\) chia hết cho đa thức \(B.\)

b. Phép chia \(ax^n\) cho \(bx^m\)

Cho hai đơn thức \(ax^m\) và \(bx^n\) (\(m,n\inℕ;a,b\inℝ,b\ne0\)). Khi đó nếu \(m\ge n\) thì phép chia \(ax^m\) cho \(bx^n\) là phép chia hết và ta có:

\(ax^m:bx^n=\dfrac{a}{b}x^{m-n}\) (quy ước \(x^0=1\))

Ví dụ: Thực hiện phép chia sau:

a) \(\left(-3x^2\right):\left(2x\right)\)                                 b) \(0,5x^4:\left(-2x^2\right)\)

Giải

Ta có:

a)   \(\left(-3x^2\right):\left(2x\right)=\dfrac{-3}{2}x^{2-1}=\dfrac{-3}{2}x\).

b) \(0,5x^4:\left(-2x^2\right)=\dfrac{0,5}{-2}x^{4-2}=\dfrac{-1}{4}x^2.\)

2. CHIA ĐA THỨC CHO ĐA THỨC, TRƯỜNG HỢP CHIA HẾT

Cách đặt tính chia

Ví dụ. Để chia đa thức \(A=6x^3-2x^2-9x+3\) cho đa thức \(B=3x-1\), ta làm như sau:

Bước 1. Đặt tính chia tương tự chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của \(A\) chia cho hạng tử bậc cao nhất của \(B\): 

\(6x^3:3x=2x^2\)

Bước 2. Lấy \(A-B.\left(2x^2\right)\) ta được 

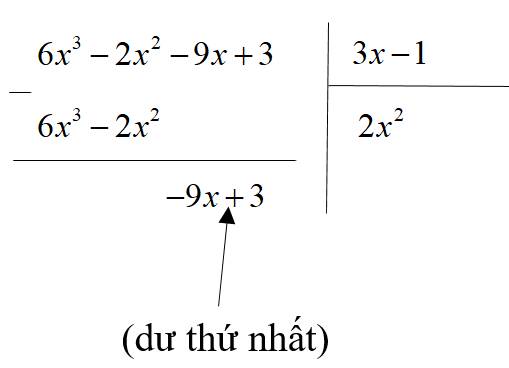
Bước 3. Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của \(B\):

\(\left(-9x\right):\left(3x\right)=-3\)

Bước 4. Lấy dư thứ nhất trừ đi tích \(B.\left(-3\right)\) ta được dư cuối cùng bằng \(0\) nên quá trình chia kết thúc

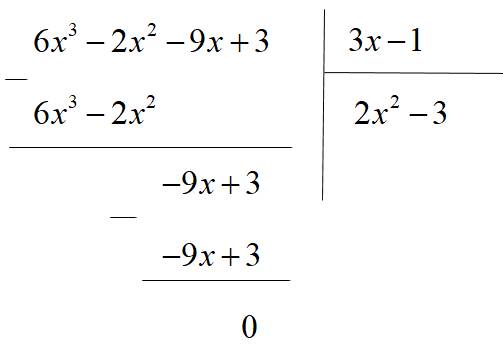
Ta được thương là đa thức \(2x^2-3.\)

Chú ý. Khi chia đa thức cho một đơn thức thì ta có thể không cần đặt tính chia.

3. CHIA ĐA THỨC CHO ĐA THỨC, TRƯỜNG HỢP CHIA CÓ DƯ

Phép chia có dư

Khi chia đa thức \(A\) cho đa thức \(B\):

Đa thức dư phải bằng \(0\) hoặc có bậc nhỏ hơn bậc của \(B.\)

Nếu thương là đa thức \(Q\), dư là \(R\) thì ta có đẳng thức \(A=BQ+R.\)

Ví dụ. Chia đa thức \(A=4x^3-2x^2-3x+7\) cho đa thức \(B=x^2-1\).

Giải

Ta có

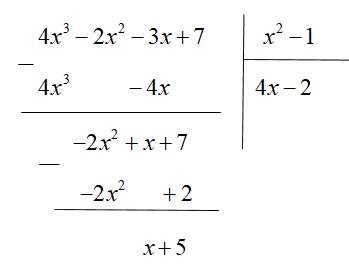
Phép chia trên gọi là phép chia có dư với đa thức thương là \(4x-2\) và đa thức dư là \(x+5.\)