Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

Với $x>0;\, x\ne 4;\, x\ne 9$ ta có:

$P=\Big(\dfrac{4\sqrt{x}}{\sqrt{x}+2}+\dfrac{8x}{4-x}\Big) \, : \, \Big(\dfrac{\sqrt{x}-1}{x-2\sqrt{x}}-\dfrac{2}{\sqrt{x}}\Big)$

$=\dfrac{4\sqrt{x}.\big(\sqrt{x}-2\big)-8x}{\big(\sqrt{x}-2\big)\big(\sqrt{x}+2\big)} \, : \, \dfrac{\sqrt{x}-1-2\big(\sqrt{x}-2\big)}{\sqrt{x}\big(\sqrt{x}-2\big)}$

$=\dfrac{-4x-8\sqrt{x}}{\big(\sqrt{x}-2\big)\big(\sqrt{x}+2\big)} \, : \, \dfrac{-\sqrt{x}+3}{\sqrt{x}\big(\sqrt{x}-2\big)}$

$=\dfrac{-4\sqrt{x}\big(\sqrt{x}+2\big)}{\big(\sqrt{x}-2\big)\big(\sqrt{x}+2\big)}.\dfrac{\sqrt{x}\big(\sqrt{x}-2\big)}{-\sqrt{x}+3}$

$=\dfrac{-4x}{-\sqrt{x}+3}=\dfrac{4x}{\sqrt{x}-3}$.

Hướng dẫn giải:

a) Với $m=-2$, phương trình (1) trở thành $x^2+2x-3=0.$

Giải ra được $x=1,\,x=-3.$

Vậy với $m=-2$ phương trình (1) có tập nghiệm là $\left\{ 1;-3 \right\}$.

b) Ta có: $\Delta =m^2-4m+4=(m-2)^2 \ge 0,\,\forall m$

Do đó phương trình $(1)$ luôn có hai nghiệm $x_1;\,x_2$ với mọi $m$.

Áp dụng hệ thức Viète, ta có: $\left\{ \begin{aligned} & x_1+x_2=m \\ & x_1x_2=m-1 \\ \end{aligned} \right.$

Biến đổi $A=\dfrac{2x_1x_2+3}{x_{1}^{2}+x_{2}^{2}+2(x_1x_2+1)}$

$=\dfrac{2x_1x_2+3}{{{(x_1+x_2)}^{2}}+2}$

$=\dfrac{2(m-1)+3}{m^2+2}$

$=\dfrac{2m+1}{m^2+2}$

$A=\dfrac{m^2+2-(m-1)^2}{m^2+2}=1-\dfrac{(m-1)^2}{m^2+2}$

Lập luận chỉ ra $A \le 1$, dấu "=" xảy ra khi $m=1$.

Hướng dẫn giải:

Gọi vận tốc của bạn Hoa lúc đi là $x$ (km/h; $x>0$).

Thời gian bạn Hoa đi từ nhà đến địa điểm A là $\dfrac{24}{x}$ (giờ).

Thời gian bạn Hoa đi một nửa quãng đường lúc về là $\dfrac{12}{x}$ (giờ).

Vận tốc của bạn Hoa đi một nửa quãng đường còn lại lúc về là $x+4$ (km/h).

Thời gian bạn Hoa đi nửa quãng đường còn lại lúc về nhà là $\dfrac{12}{x+4}$ (giờ).

Do thời gian về ít hơn thời gian đi là $15$ phút $\Big($đổi bằng $\dfrac{1}{4}$ h$\Big)$ nên ta có phương trình:

$\dfrac{24}{x}-\dfrac{12}{x}-\dfrac{12}{x+4}=\dfrac{1}{4}$

$\dfrac{12}{x}-\dfrac{12}{x+4}=\dfrac{1}{4}$

${{x}^{2}}+4x-192=0$

$x=12$ hoặc $x=-16$

Ta thấy $x=-16$ không thỏa mãn.

Vậy vận tốc của bạn Hoa lúc đi là $12$ km/h.

Hướng dẫn giải:

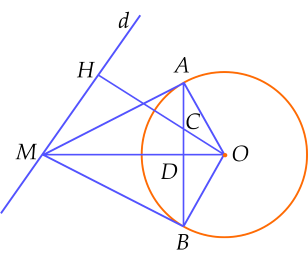
a) Do $MA$, $MB$ là hai tiếp tuyến của đường tròn $(O)$ nên $MA \bot OA;\,MB\bot OB\,$

Suy ra $\widehat{MAO}=\widehat{MBO}=90^\circ$.

Gọi $I$ là trung điểm của $OM$.

Xét tam giác $MAO$ vuông tại $A$, $AI$ là trung tuyến ứng với cạnh huyền, ta có:

$AI=MI=IO=\dfrac{1}{2}OM$ (1)

Xét tam giác $MBO$ vuông tại $B$, $BI$ là trung tuyến ứng với cạnh huyền, ta có:

$BI=MI=IO=\dfrac{1}{2}OM$ (2)

Từ (1) và (2) suy ra $AI=MI=IO=BI$

Vậy tứ giác $MAOB$ nội tiếp đường tròn tâm $I$, đường kính $OM$.

b) Do $MA$, $MB $ là hai tiếp tuyến của đường tròn $(O)$ nên $MA = MB$;

Mà $OA = OB = R$ nên $MO$ là trung trực của đoạn thẳng $AB$.

Suy ra $MO\bot AB$ tại $D$.

$H$ là hình chiếu của $O$ trên đường thẳng $d$ nên $HO\bot MH$.

Xét tam giác $\Delta ODC$ và $\Delta OHM$ có:

$\widehat{MOH}$ chung;

$\widehat{ODC}=\widehat{OHM}=90^\circ$

Suy ra $\Delta ODC \backsim \Delta OHM$ (g.g) suy ra $\dfrac{OD}{OH}=\dfrac{OC}{OM}$

Hay $OC.OH=OD.OM$.

Tương tự, chứng minh $\Delta ODA \backsim \Delta OAM$ suy ra $OD.OM=OA^2 = R^2$

Hay $OC.OH=R^2$

c) Vì điểm $O$ và đường thẳng $d$ cố định nên $H$ cố định do đó $OH$ cố định và có độ dài không đổi suy ra $C\in OH$ cố định (3)

 Từ $OC.OH=R^2$ ta có $OC=\dfrac{R^2}{OH}$ không đổi (4)

Từ (3) và (4) suy ra điểm $C$ cố định suy ra dây $AB$ luôn đi qua điểm $C$ cố định.

Vậy khi điểm $M$ di chuyển trên đường thẳng $d$ thì dây $AB$ luôn đi qua một điểm cố định.

Hướng dẫn giải:

Ta có: $(x^2-1)(x+3)(x+5)=m$ (1)

$(x+1)(x+3)(x-1)(x+5)=m$

$(x^2+4x+3)(x^2+4x-5)=m$ (2)

Đặt $y=x^4+4x+4=(x+2)^2 \ge 0$ với mọi $x$. 

Khi đó (2) có dạng: $(y-1)(y-9)=m$ hay $y^2-10y+9-m=0$ (3)

Phương trình (1) có bốn nghiệm phân biệt tương đương với phương trình (3) có hai nghiệm dương phân biệt $y_1>y_2>0$ khi và chỉ khi

$\left\{ \begin{aligned}   & \Delta '=16+m>0 \\  & y_1+y_2=10>0 \\  & y_1y_2=9-m>0 \\ \end{aligned} \right.$ hay $-16<m<9$ (4)

Khi $y_1; \, y_2$ là hai nghiệm dương phân biệt của phương trình (3) thì phương trình (2) tương đương với:

$x^2+4x+4-y_1=0$ hoặc $x^2+4x+4-y_2=0$

Gọi $x_1,\,x_2$ là hai nghiệm phân biệt của phương trình: $x^2+4x+4-y_1=0$ (5)

Gọi $x_3,\,x_4$ là hai nghiệm phân biệt của phương trình: $x^2+4x+4-y_2=0$ (6)

Áp dụng định lí Viète cho các phương trình (3), (5), (6) ta có:

$\dfrac{1}{x_1}+\dfrac{1}{x_2}+\dfrac{1}{x_3}+\dfrac{1}{x_4}$

$=\dfrac{x_1+x_2}{x_1x_2}+\dfrac{x_3+x_4}{x_3x_4}$

$=\dfrac{-4}{4-y_1}+\dfrac{-4}{4-y_2}$

$\dfrac{4(y_1+y_2)-32}{16-4(y_1+y_2)+y_1y_2}$

$=\dfrac{40-32}{16-40+9-m}$

$=\dfrac{8}{-15-m}=-1$

Suy ra $m=-7$ (thỏa mãn).