Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

1.

Ta có:

$\left\{ \begin{aligned}  & 2x+3y=-2 \\  & 4x+y=1 \end{aligned} \right.$

$ \left\{ \begin{aligned}  & 4x+6y=-4 \\  & 4x+y=1 \end{aligned} \right.$

$\left\{ \begin{aligned}  & 5y=-5 \\  & 4x+y=1 \end{aligned} \right.$

$ \left\{ \begin{aligned}  & y=-1 \\  & 4x-1=1 \end{aligned} \right.$

$ \left\{ \begin{aligned}& y=-1 \\ & 4x=1+1 \end{aligned} \right.$

$\left\{ \begin{aligned} & x=\dfrac{1}{2} \\  & y=-1 \end{aligned} \right.$

Vậy hệ phương trình có nghiệm $(x;\,y)=\Big(\dfrac{1}{2};\,-1\Big)$.

2.

a) Với $x > 0; x \ne 4$ ta có:

$P=\Big( \dfrac{x}{x\sqrt{x}-4\sqrt{x}}-\dfrac{6}{3\sqrt{x}-6} + \dfrac{1}{\sqrt{x} + 2} \Big) : \Big( \sqrt{x} – 2 + \dfrac{10-x}{\sqrt{x}+2}\Big)$

$=\Big[ \dfrac{x}{\sqrt{x}(x-4)} - \dfrac{6}{3(\sqrt{x}-2)}-\dfrac{1}{\sqrt{x} + 2} \Big] : \Big(\dfrac{x-4+10-x}{\sqrt{x} + 2} \Big)$

$ = \Big[\dfrac{\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)} - \dfrac{2}{\sqrt{x}-2} + \dfrac{1}{\sqrt{x}+2} \Big] : \dfrac{6}{\sqrt{x}+2}$

$=\dfrac{\sqrt{x}-2(\sqrt{x}+2)+\sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}+2)}:\dfrac{6}{\sqrt{x}+2}$

$=\dfrac{\sqrt{x}-2\sqrt{x}-4+\sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}+2)}:\dfrac{6}{\sqrt{x}+2}$

$=\dfrac{-6}{(\sqrt{x}-2)(\sqrt{x}+2)}.\dfrac{\sqrt{x}+2}{6}$

$=\dfrac{-1}{\sqrt{x}-2}$.

Vậy $P=\dfrac{-1}{\sqrt{x}-2}$.

b) Với  $x > 0; x \ne 4$. Ta có

$Q= (-\sqrt{x}-1).P= (-\sqrt{x}-1).\dfrac{-1}{\sqrt{x}-2} = \dfrac{\sqrt{x}+1}{\sqrt{x}-2}=1+\dfrac{3}{\sqrt{x}-2}$.

+ Nếu $x$ không là số chính phương, suy ra $\sqrt{x}$ là số vô tỉ.

Do đó $Q$ không nguyên.

+ Nếu $x$ là số chính phương, suy ra $\sqrt{x}$ là số nguyên.

Do đó $Q$ nguyên hay $\dfrac{3}{\sqrt{x}-2}$ nguyên khi và chỉ khi $\sqrt{x}-2$ thuộc ước của $3$

Giải ra tìm được các giá trị $x = 1; x = 9; x = 25$ (TMĐK).

Vậy $x = 1; x = 9; x = 25$.

Hướng dẫn giải:

Gọi số luống rau trong vườn nhà Mai là $x$  ($x\in N,x>5$)

Gọi số cây rau trồng trên mỗi luống là $y$ ($y\in N,y>2$)

Tổng số cây rau bắp cải trong vườn nhà Mai là $xy$

Theo bài ra ta có hệ phương trình $\left\{ \begin{aligned}  & xy-(x+7)(y-2)=9 \\  & (x-5)(y+2)-xy=15 \end{aligned} \right.$

$\Leftrightarrow \left\{ \begin{aligned}  & 2x-7y=-5 \\  & 2x-5y=25 \end{aligned} \right.$

Giải hệ phương trình tìm được $\left\{ \begin{aligned}  & x=50 \\  & y=15 \end{aligned} \right.$ (thoả mãn điều kiện của ẩn)

Vậy tổng số cây rau bắp cải trong vườn nhà Mai là $50.15=750$ cây.

Hướng dẫn giải:

Gọi vị trí ban đầu của người đó là điểm $A$.

Vì thời gian thực hiện mỗi vòng của đu quay là $30$ phút nên khi đu quay quay đều thì $10$ phút người đó đi được $\dfrac{1}{3}$ vòng tròn và đang ở vị trí điểm $B$ như hình vẽ sau:

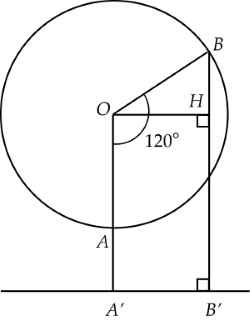
Gọi $A', B'$ lần lượt là hình chiếu của $A, B$ trên mặt đất, kẻ $OH\bot BB'$.Ta có: $\widehat{AOB}=\dfrac{1}{3}.360^\circ=120^\circ, OA'=80$ m.

Vì $OA'B'H$ là hình chữ nhật (tứ giác có ba góc vuông) nên $HB'=OA'=80$ (m).

Ta có: $\widehat{AOH}=90^\circ$

$\widehat{BOH}=120^\circ−90^\circ=30^\circ $

Xét tam giác vuông $OBH$ có: 

$BH=OB.\sin30^\circ=75.\dfrac{1}{2}=37,5$ (m)

$BB'=BH+HB'=37,5+80=117,5$ (m).

Vậy sau $10$ phút người đó ở độ cao $117,5$ m so với mặt đất.

Hướng dẫn giải:

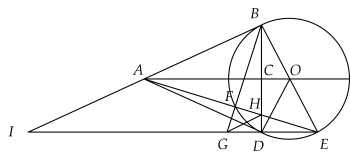
a) Ta có: $OB = OD (= R)$ nên $\Delta ODB$ cân tại $O$.

Mà $OC$ là đường cao của $\Delta ODB$.

Nên $OC$ cũng là đường phân giác của $\Delta ODB$.

Suy ra $\widehat{BOC}=\widehat{COD}$ hay $\widehat{BOA}=\widehat{AOD}$.

Xét $\Delta ABO$ và $\Delta ADO$ có:

$OB = OD (= R)$

$\widehat{BOA}=\widehat{AOD}$ (chứng minh trên)

Cạnh $OA$ chung

Do đó $\Delta ABO = \Delta ADO$ (c-g-c)

Suy ra $\widehat{ABO}=\widehat{ADO}=90^\circ$.

Do đó $AD$ là tiếp tuyến của $(O)$.

Ta có: $\widehat{DEB}=\dfrac12 sđ\overset\frown{BD} \, \, (1)$

Lại có: $\widehat{BOD} = sđ \overset\frown{BD}$

Mà $\widehat{BOA} = \dfrac{1}{2} \widehat{BOD}$

Nên $\widehat{BOA} = \dfrac12 sđ \overset\frown{BD} \, \,  (2)$

Từ $(1)$ và $(2)$ suy ra $\widehat{BOA}=\widehat{DEO}$.

Mà hai góc này nằm ở vị trí đồng vị nên $OA // DE$.

b) Vì $F$ thuộc đường tròn đường kính $BE$ nên $\widehat{BFE}=90^\circ$

Xét $\Delta ABE$ vuông tại $B$ có: $BF$ là đường cao

Suy ra $AE . AF = AB^2$

Chứng minh tương tự, ta có: $AC . AO = AD^2.$

Mà $AB = AD$ (tính chất hai tiếp tuyến cắt nhau)

Do đó $AB^2 = AD^2$

Suy ra: $AE . AF = AC.AO$.

c) Vì $D$ thuộc đường tròn đường kính BE nên $\widehat{BDE}=90^\circ$.

Ta có: $BD$ là đường cao của $\Delta BGE$; $EF$ là đường cao của $\Delta BGE$.

Mà $BD, EF$ cắt nhau tại $H$.

Do đó $H$ là trực tâm của $\Delta BGE$.

Suy ra: $GH \bot BE; AB \bot BE$

Nên $GH // AB$.

Xét $\Delta BIE $có: $BO = EO (= R);\, AO // EI (AO // DE)$.

Do đó $AB = AI$.

Hướng dẫn giải:

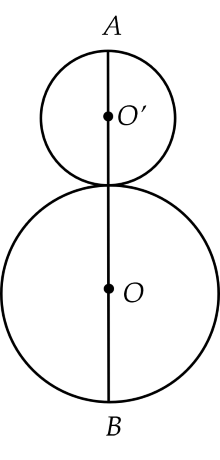
Ta có: $1,8$ m$ = 180$ cm

Gọi $r$ (cm) là bán kính của đường tròn nhỏ

Đường kính của đường tròn nhỏ là $2r$ (cm) $(r > 0) $

Đường kính của đường tròn lớn là: $2.2r = 4r$ (cm)

Ta có: $2r + 4r = 180$ (vì $(O)$ tiếp xúc với $(O’)$)

$6r=180$

$r=30$ cm.

Vậy để đắp người tuyết có chiều cao là $1,8$ m thì ta cần đắp hai quả cầu tuyết có đường kính lần lượt là $60$ cm và $120$ cm.