Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (8 điểm) SVIP
Câu 13. Viết bất đẳng thức để mô tả mỗi tình huống sau:
a) Tuần tới, nhiệt độ $t$ ($^\circ C$) tại Tokyo là trên $-5^\circ C$.
b) Để được điều khiển xe máy điện thì tuổi $x$ của một người phải ít nhất là $16$ tuổi.
c) Mức lương tối thiểu trong một giờ làm việc của người lao động là $20\,000$ đồng.
d) $y$ là số dương.
Hướng dẫn giải:
a) $t>-5$.
b) $x\ge 16$.
c) Với $y$ (đồng) là mức lương tối thiểu cho một giờ làm việc của người lao động, ta có bất đẳng thức $y\ge 20\,\,000$.
d) $y>0$.
Câu 14. (2,0 điểm). Giải các phương trình và hệ phương trình sau:
a) $\dfrac{x+6}{x+5}+\dfrac{3}{2}=2$;
b) $\left\{ \begin{aligned} & x+3y=-2 \\ & 5x+8y=11 \\ \end{aligned} \right.$.
Hướng dẫn giải:
a) Điều kiện xác định: $x\ne -5$
Ta có: $\dfrac{x+6}{x+5}+\dfrac{3}{2}=2$
$\dfrac{x+6}{x+5}=\dfrac{1}{2}$
$2( x+6)=x+5$
$2x+12=x+5$
$x=-7$ (thỏa mãn điều kiện)
Vậy phương trình đã cho có nghiệm $x=-7$.
b) $\left\{ \begin{aligned} & x+3y=-2 \\ & 5x+8y=11 \\ \end{aligned} \right.$
$\left\{ \begin{aligned} & -5x-15y=10 \\ & 5x+8y=11 \\ \end{aligned} \right.$
$\left\{ \begin{aligned} & -7y=21 \\ & 5x+8y=11 \\ \end{aligned} \right.$
$\left\{ \begin{aligned} & y=-3 \\ & 5x+8.( -3)=11 \\ \end{aligned} \right.$
$\left\{ \begin{aligned} & y=-3 \\ & x=7 \\ \end{aligned} \right.$
Vậy hệ phương trình đã cho có nghiệm $( x;y)=( 7;-3)$.
Câu 15. (1,0 điểm). Một người đi xe máy từ địa điểm A đến địa điểm B cách nhau $60$ km. Khi từ B trở về A, do trời mưa người đó giảm tốc độ $10$ km/h so với lúc đi nên thời gian về nhiều hơn thời gian đi là $30$ phút. Tính tốc độ lúc về của người đó.
Hướng dẫn giải:
Gọi tốc độ của xe máy lúc về là $x$ (km/h), $x>0$
Tốc độ của xe máy lúc đi là: $x + 10$ (km/h)
Thời gian của xe máy lúc đi là $\dfrac{60}{x+10}$ (h)
Thời gian của xe máy lúc về là $\dfrac{60}{x}$ (h)
Theo bài ra ta có phương trình:
$\dfrac{60}{x}-\dfrac{60}{x+10}=\dfrac{1}{2}$
$\dfrac{120x+1200}{2x( x+10)}-\dfrac{120x}{2x( x+10)}=\dfrac{x( x+10)}{2x( x+10)}$
$120x+1200-120x=x( x+10)$
${{x}^{2}}+10x=1\,200$
${{x}^{2}}+10x+25=1 \, 225$
${{( x+5)}^{2}}=1\,\,225$
$ \left[ \begin{aligned} & x+5=35 \\ & x+5=-35 \\ \end{aligned} \right.$
$\left[ \begin{aligned} & x=30 \\ & x=-40 \\ \end{aligned} \right. $
Đối chiếu điều kiện, ta có: $x = 30$ thỏa mãn.
Vậy tốc độ của xe máy lúc về là $30$ km/h.
Câu 16. (2,0 điểm)
1. So sánh $\sin 35^\circ$ và $\cos 55^\circ$;
$\tan 28^\circ$ và $\cot 62^\circ$.
2. Cho tam giác $ABC$ vuông tại $A$ có cạnh huyền bằng $20$ cm, $\widehat{B}=36^\circ$. Giải thích vì sao $AB \approx 16,18$ cm.
Hướng dẫn giải:
1) $\sin 35^\circ = \cos (90^\circ-35^\circ)=\cos 55^\circ$;
$\tan 28^\circ = \cot (90^\circ-28^\circ)=\cot 62^\circ$.
2) Xét $\Delta ABC$ vuông tại $A$, ta có:
$BC=20$
$\cos \widehat{B}=\dfrac{AB}{BC}=\dfrac{AB}{20}=\cos 36^\circ$
Suy ra $AB=BC.\cos 36^\circ \approx 16,18$ cm.
Câu 17. (1,0 điểm). Người ta cần lắp đặt một thiết bị chiếu sáng gắn trên tường cho một phòng triển lãm. Thiết bị này có góc chiếu sáng là $20^\circ$ và cần đặt cao hơn mặt đất là $2,5$ m. Người ta đặt thiết bị này sát tường và căn chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường $2$ m.
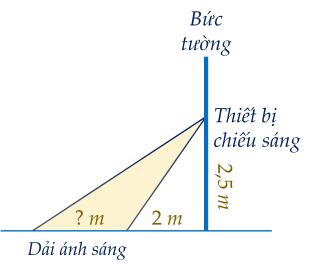
Tính độ dài vùng được chiếu sáng trên mặt đất.
Hướng dẫn giải:
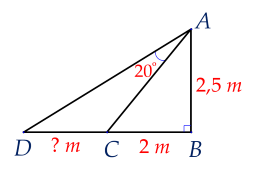
Xét $\Delta ABC$ vuông tại $B$, ta có:
$\tan \widehat{BAC}=\dfrac{BC}{AB}=\dfrac{2}{2,5}=0,8$ (tỉ số lượng giác của góc nhọn)
Suy ra $\widehat{BAC} \approx 38,7^\circ $
Ta có: $\widehat{BAD}=\widehat{BAC}+\widehat{CAD}=38,7^\circ +20^\circ =58,7^\circ $
Xét $\Delta ABD$ vuông tại $B$, ta có:
$\tan \widehat{BAD}=\dfrac{BD}{AB}$ (tỉ số lượng giác của góc nhọn)
Suy ra $BD=AB.\tan \widehat{BAD}=2,5.\tan 58,7^\circ \approx 4,1$ m.
$CD=BD-BC=4,1-2=2,1$ m.
Vậy độ dài vùng được chiếu sáng trên mặt đất là $2,1$ m.
