Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Câu 13. (1 điểm) Một ca nô đi xuôi dòng trong $2$ giờ $30$ phút. Biết rằng tốc độ ca nô khi nước yên lặng không quá $40$ km/h và tốc độ của dòng nước là $6$ km/h. Chứng minh quãng đường ca nô đi được trong thời gian trên không vượt quá $115$ km.
Hướng dẫn giải:
Gọi tốc độ của ca nô khi nước yên lặng là $x$ (km/h) ($x>6$ ).
Tốc độ ca nô đi xuôi dòng là $x+6$ (km/h)
Ta có $x\le 40$ nên $x+6\le 40+6$, tức là $x+6\le 46$
Gọi $s$ (km) là quãng đường ca nô đi được trong $2$ giờ $30$ phút $=2,5$ giờ
Ta có $s=2,5.(x+6)$ (km).
Do $x+6\le 46$ nên $2,5.(x+6)<2,5.46$ hay $s\le 115$
Vậy quãng đường ca nô đi được trong $2$ giờ $30$ phút không vượt quá $115$ km.
Câu 14. (2,0 điểm). Giải các phương trình và hệ phương trình sau:
a) ${{\left( 2x+1 \right)}^{2}}-9{{x}^{2}}=0$
b) $\left\{ \begin{aligned} & 5x-4y=3 \\ & 2x+y=4 \\ \end{aligned} \right.$
Hướng dẫn giải:
a) Ta có $(2x+1)^2-9x^2=0$
$(2x+1-3x)(2x+1+3x)=0$
$(-x+1)(5x+1)=0$
+ Giải phương trình $-x+1=0$
$x=1$
+ Giải phương trình $5x+1=0$
$x=\dfrac{-1}{5}$
Vậy phương trình có hai nghiệm là $x=1$ và $x=\dfrac{-1}{5}$.
b) Ta có: $\left\{ \begin{aligned} & 5x-4y=3 \\ & 2x+y=4 \\ \end{aligned} \right.$
$ \left\{ \begin{aligned} & 5x-4y=3 \\ & 8x+4y=16 \\ \end{aligned} \right.$
$\left\{ \begin{aligned} & 13x=19 \\ & 2x+y=4 \\ \end{aligned} \right.$
$\left\{ \begin{aligned} & x=\dfrac{19}{13} \\ & y=\dfrac{14}{13} \\ \end{aligned} \right.$
Vậy hệ phương trình đã cho có nghiệm $(x; y) = \Big( \dfrac{19}{13};\dfrac{14}{13} \Big) $.
Câu 15. (1,0 điểm). Trong một đợt khuyến mại, siêu thị giảm giá cho mặt hàng $A$ là $20\%$ và mặt hàng $B$ là $15\%$ so với giá niêm yết. Một khách hàng mua hai món hàng $A$ và một món hàng $B$thì phải trả số tiền là $362 \, 000$ đồng. Nhưng nếu mua trong khung giờ vàng thì mặt hàng $A$ được giảm giá $30\%$ và mặt hàng $B$ được giảm giá $25\%$ so với giá niêm yết. Một khách hàng mua ba món hàng $A$ và hai món hàng $B$ trong khung giờ vàng nên phải trả số tiền là $552\,000$ đồng. Tính giá niêm yết của mỗi mặt hàng $A$ và $B$.
Hướng dẫn giải:
Gọi $x,\,y$(đồng) lần lượt là giá niêm yết của mỗi mặt hàng $A$ và $B$ $(x>0,\,y>0)$
Một khách hàng mua hai món hàng $A$ và một món hàng $B$ thì phải trả số tiền là $362 \, 000$ đồng nên ta có:
$80\%x\,.\,2+85\%y=362\,000$ hay $1,6x+0,85y=362\,000$ (1)
Trong khung giờ vàng khách hàng mua ba món hàng $A$ và hai món hàng $B$ trong khung giờ vàng nên phải trả số tiền là $552\,000$ đồng nên ta có:
$70\%x\,.\,3+75\%y.2=552\,000$ hay $2,1x+1,5y=552 \, 000$ (2)
Từ (1) và (2) ta có hệ phương trình: $\left\{ \begin{aligned} & 1,6x+0,85y=362\,000 \\ & 2,1x+1,5y=552\,000 \\ \end{aligned} \right.$
Giải hệ phương trình ta được: $\left\{ \begin{aligned} & x=120\,000 \\ & y=200\,000 \\ \end{aligned} \right.$
Vậy giá niêm yết của mặt hàng $A$ là $120\,000$ đồng, mặt hàng $B$ là $200\,000$ đồng.
Câu 16. (2,0 điểm). Cho hình bình hành $ABCD$ có đường chéo $AC$ lớn hơn đường chéo $BD$. Kẻ $CH \bot AD$ và $CK \bot AB$.
a) Chứng minh $\Delta CKH \backsim \Delta BCA$.
b) Chứng minh $HK=AC.\sin \widehat{BAD}$.
Hướng dẫn giải:
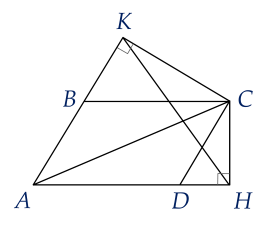
a) $\Delta BKC \backsim \Delta DHC$ (g. g)
Vì $\widehat{K}=\widehat{H}= 90^\circ$
$\widehat{D}=\widehat{B}$ (cùng bằng $\widehat{A}$)
$\dfrac{KC}{HC}=\dfrac{BC}{DC}$ hay $\dfrac{KC}{HC}=\dfrac{BC}{AB}$ (*)
Xét tứ giác $AKCH$ có: $\widehat{A}+\widehat{HCK}=180^\circ$;
$\widehat{A}+\widehat{ABC}=180^\circ$
Suy ra: $\widehat{ABC}=\widehat{HCK}$ (**)
Từ (*) và (**) suy ra: $\Delta CKH \backsim \Delta BCA$ (c-g-c)
b) $\Delta CKH \backsim \Delta BCA$ suy ra $\dfrac{HK}{AC}=\dfrac{CK}{BC}$
$HK=AC.\dfrac{CK}{BC}=AC.\sin \widehat{KBC}$ mà $\widehat{BAD}=\widehat{KBC}$ (cặp góc đồng vị) nên $HK=AC.\sin \widehat{BAD}$.
Câu 17. (1,0 điểm). Hai chiếc tàu thủy $B$ và $C$ cùng xuất phát từ một vị trí $A$, đi thẳng theo hai hướng tạo thành một góc $60^\circ$ (Hình vẽ).
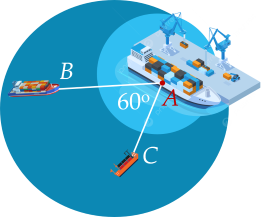
Tàu $B$ chạy với tốc độ $20 $ hải lí/giờ, tàu $C$ chạy với tốc độ $15$ hải lí/giờ. Sau $1,5$ giờ hai tàu $B$ và $C$ cách nhau bao nhiêu hải lí (kết quả làm tròn đến hàng phần trăm)?
Hướng dẫn giải:
Nối $B$ và $C$. Kẻ $CH \perp AB$ ($H \in AB$).
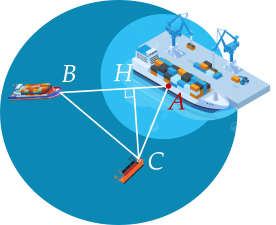
Sau $1,5$ giờ tàu $B$ chạy được quãng đường là: $AB = 20.1,5 = 30$ (hải lí).
Sau $1,5$ giờ tàu $C$ chạy được quãng đường là: $AC = 15.1,5 = 22,5$ (hải lí).
Xét tam giác $AHC$ vuông tại $H$, ta có:
$CH = AC. \sin A = 22,5. \sin 60^\circ = \dfrac{45\sqrt{3}}{4}$ (hải lí).
$AH = AC.\cos A = 22,5.\cos 60^\circ = 11,25$ (hải lí).
Do đó $BH = AB - AH = 30 - 11,25 = 18,75$ (hải lí).
Mặt khác, tam giác $CHB$ vuông tại $H$, áp dụng định lí Pythagore ta có:
$BC=\sqrt{BH^2+CH^2}=\sqrt{(18,75)^2+\Big(\dfrac{45\sqrt{3}}4\Big)^2}\approx 27,04$ (hải lí).
Vậy sau $1,5$ giờ tàu $B$ cách tàu $C$ là $27,04$ hải lí.
