Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

a) Tập hợp ${M}$ gồm các kết quả có thể xảy ra khi bút màu được rút ra là:

${M}=$ $\{$ xanh, đỏ, vàng, da cam, tím, trắng, hồng $\}$.

b) Số phần tử của tập hợp ${M}$ là $7$.

Xác suất biến cố "Màu được rút ra là vàng" là: $\dfrac{1}{7}$

Hướng dẫn giải:

a) Sắp xếp ${P(x)}$ và ${Q(x)}$ theo lũy thừa giảm dần.

$P(x)=2 x^3+5 x^2-2 x+2$.

$Q(x)=-x^3-5 x^2+2 x+6$.

b) $P(x)+Q(x)=x^3+8$.

$P(x)-Q(x)=3 x^3+10 x^2-4 x-4$.

Hướng dẫn giải:

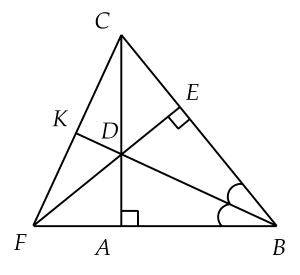
a) Xét $\Delta BAD$ và $\Delta BED$ lần lượt vuông tại $A$ và $E$.

    $BD$ chung.

    $\widehat{ABD}=\widehat{EBD} $ ($BD$ là tia phân giác).

Suy ra $\Delta BAD= \Delta BED$ (cạnh huyền - góc nhọn).

b) Vì $\Delta {BAD}=\Delta {BED}({c} / {m}$ phần a) nên ${AD}={ED} ; {BA}={BE}$ (2)

Xét $\Delta {AFD}$ vuông tại ${A}$ và $\Delta {ECD}$ vuông tại ${E}$ có:

    ${AD}={ED}({cmt})$

    $\widehat{A D F}=\widehat{E D C}$ (đối đỉnh)

Suy ra $\Delta {AFD}=\Delta {ECD}$ (cạnh góc vuông - góc nhọn)

Nên $A F=E C$ (2).

Từ (1) và (2) suy ra ${AF}+{BA}={BE}+{EC}$

Hay ${BF}={BC}$

Vậy $\Delta B C F$ cân tại $B$.

c) Giả sử ${BD}$ kéo dài cắt ${FC}$ tại ${K}$

Xét $\Delta B K F$ và $\Delta B K C$ có:

    ${BK}$ là cạnh chung

    $\widehat{K B F}=\widehat{K B C}$ (Vì ${BD}$ là phân giác của $\widehat{A B C}$ )

     ${BF}={BC}$ ( chứng minh phần ${b})$

Suy ra $\Delta B K F=\Delta B K C($ c.g.c $)$

Suy ra ${KF}={KC}$ (hai cạnh tương ứng)

Vậy ${BK}$ hay ${BD}$ là đường trung tuyến của $\Delta {BCF}$.

Hướng dẫn giải:

Biểu thức $A$ lớn nhất khi và chỉ khi ${x}^{2022}+2023$ nhỏ nhất.

Ta có: ${x}^{2022} \geq 0$ với mọi $x$. Dấu bằng xảy ra khi và chỉ khi $x=0$.

Vậy khi $x=0$, $A$ đạt giá trị lớn nhất bằng $2023$.