Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (3 điểm) SVIP
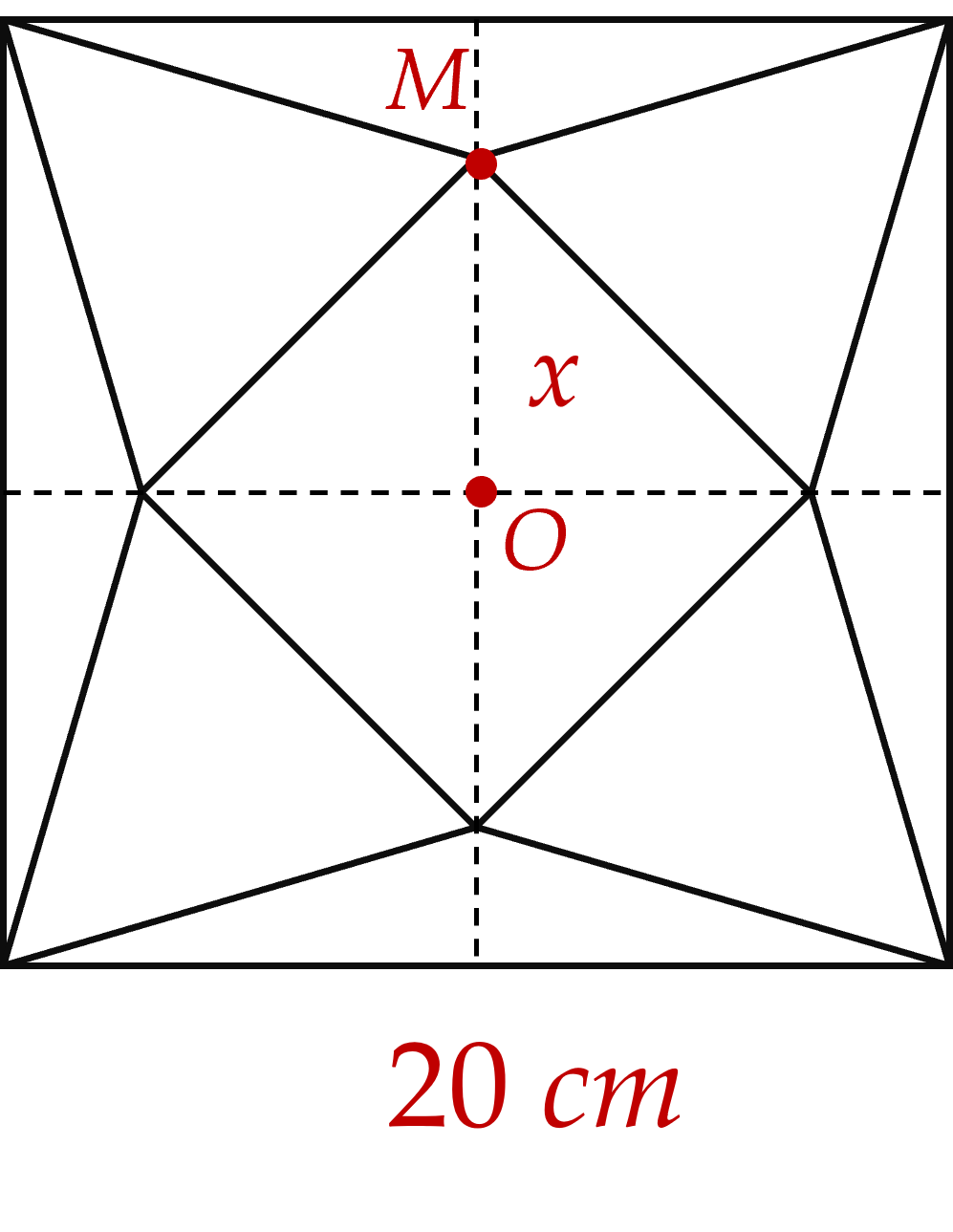
Cắt một miếng giấy hình vuông và xếp thành một hình chóp tứ giác đều (hình vẽ). Biết cạnh hình vuông bằng $20$ (cm), $OM=x$ (cm). Tìm $x$ để hình chóp đều ấy có thể tích lớn nhất.
Hướng dẫn giải:
Sau khi cắt miếng giấy hình vuông như trên, ta xếp lại được hình chóp tứ giác đều $S.MNPQ$

Ta có $OM=x\Rightarrow MP=NQ=2x$ (cm)
Mà $NQ=MN\sqrt{2}\Rightarrow MN=\sqrt{2}x$ (cm)
Gọi $H$ là trung điểm $PQ$
$OH=\dfrac{NP}{2}=\dfrac{\sqrt{2}}{2}x$ (cm)
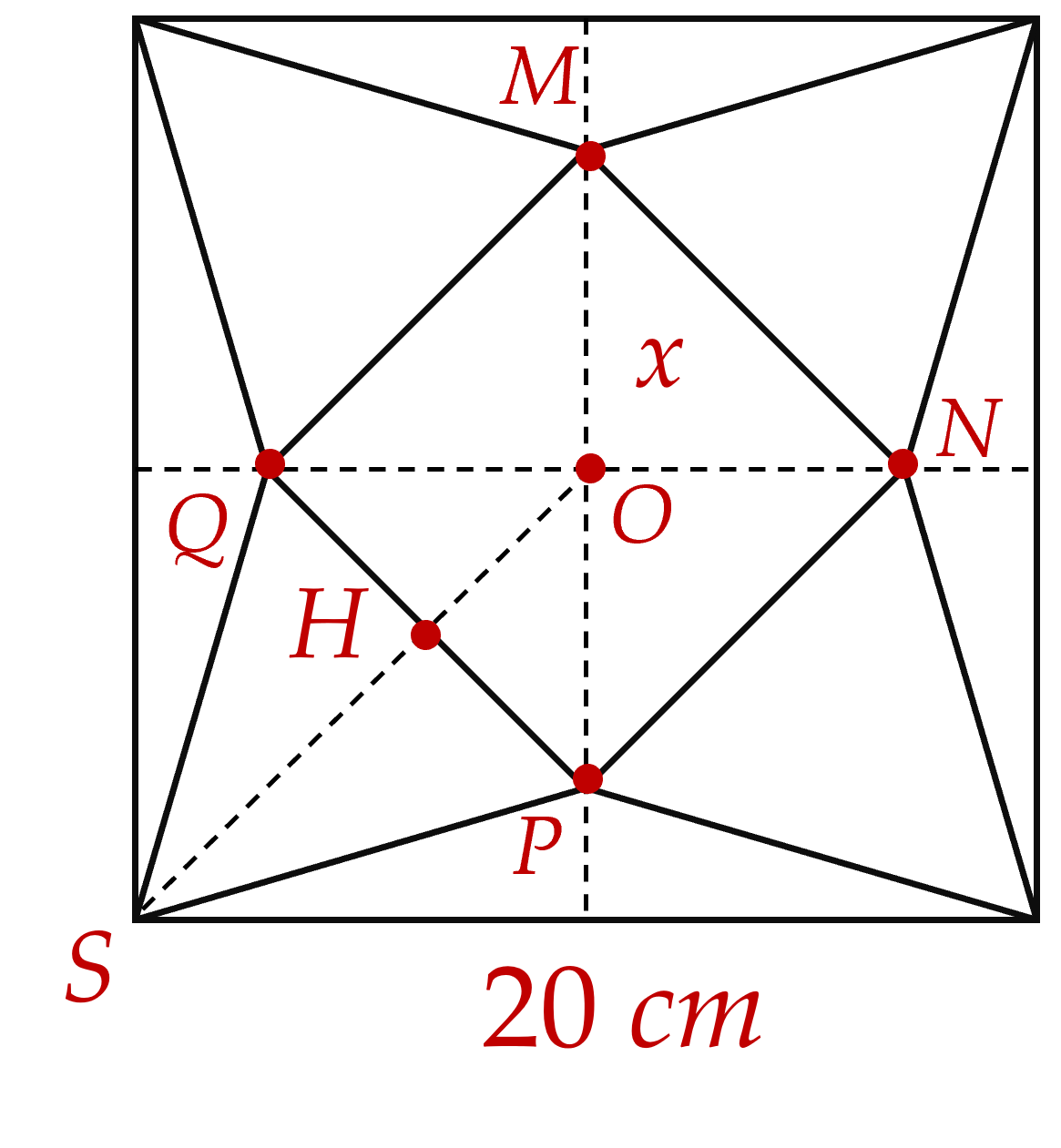
Từ hình vẽ trên, ta có: $SH=SO-OH=10\sqrt{2}-\dfrac{\sqrt{2}x}{2}$ (cm)
SO lúc này là một nửa hình đường chéo hình vuông cạnh $20$ cm
Suy ra, chiều cao hình chóp là:
$SO_{h}=\sqrt{SH^2-OH^2}=\sqrt{20(10-x)}$ (cm)
Thể tích khối chóp $S.MNPQ$ là:
$V=\dfrac{1}{3}SO.{{S}_{MNPQ}}$
$V=\dfrac{1}{3}\sqrt{20(10-x)}.(\sqrt{2}x)^2$
$V=\dfrac{\sqrt{20}}{3}\sqrt{(40-4x).4x^4}$
$V=\dfrac{\sqrt{20}}{3}\sqrt{(40-4x).x.x.x.x}\le \dfrac{\sqrt{20}}{3}.\sqrt{{{\Bigg(\dfrac{40-4x+x+x+x+x}{5} \Bigg)}^{5}}}$
$=\dfrac{256\sqrt{10}}{3}$ (cm3)
Dấu “$=$” xảy ra khi $40-4x=x\Leftrightarrow x=8$ (cm).
Vợ chồng nhà chị Thơm vay ngân hàng $400$ triệu đồng để mua nhà với hình thức trả góp, chị chọn gói lãi suất ưu đãi cố định $0,5\%$ tháng trong $12$ tháng đầu và sang tháng thứ $13$ trở đi thì ngân hàng tính lãi suất thả nổi theo quy định. Gia đình chị hoàn nợ cho ngân hàng theo cách: sau đúng một tháng kể từ ngà̀y vay thì bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là $15$ triệu đồng. Sau khi hết $12$ tháng ưu đãi thì chị Thơm phải trả lãi suất thả nổi là $1\%$ tháng. Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó và lãi suất thả nổi của ngân hàng không thay đổi trong thời gian chị Thơm hoàn nợ. Hỏi chị Thơm cần bao nhiêu tháng để trả hết nợ ngân hàng kể từ khi vay?
Hướng dẫn giải:
Số tiền chị Thơm nợ sau một tháng là $400+400.0,5\%=400(1+0,5\%)$ (triệu đồng).
Sau 1 tháng thì số tiền chị Thơm phải trả là $400(1+0,5\%)-15$ (triệu đồng).
Sau 2 tháng thì số tiền chị Thơm phải trả là:
$400(1+0,5\%)-15+[400(1+0,5\%)-15].0,5\%-15$
$=400(1+0,5\%)^2-15[(1+0,5\%)+1]$ (triệu đồng).
Sau 12 tháng thì số tiền chị Thơm phải trà là
$A=400(1+0,5\%)^{12}-15\left[(1+0,5\%)^{11}+(1+0,5\%)^{10}+\ldots +(1+0,5\%)+1 \right]$
$=400(1+0,5\%)^{12}-15\dfrac{(1+0,5\%)^{12}-1}{(1+0,5\%)-1}$
$=400(1+0,5\%)^{12}-\dfrac{15}{0,5\%}\left[(1+0,5\%)^{12}-1 \right]$
$=239,637$ (triệu đồng).
Gọi $n$ là số tháng tiếp theo mà chị Thơm cần đề trả hết nợ, tương tự như trên ta được
$A(1+1\%)^{n}-\dfrac{15[(1+1\%)^{n}-1]}{1\%}=0$
$\Leftrightarrow n=\log _{1+1\%}\dfrac{-15}{A.1\%-15}\approx 17.49$.
Tức là chị Thơm cần thêm $18$ tháng để trả hết nợ.
Vậy chị Thơm cần $12+18=30$ tháng để trả hết nợ ngân hàng kể từ khi vay.
Cho tam giác đều $ABC$ cạnh bằng $12$. Gọi $d$ là đường thẳng đi qua $A$ và vuông góc với mặt phẳng $\left(ABC \right)$. Trên đường thẳng $d$ lấy điểm $S$, $H$ là trực tâm của tam giác $SBC$. Khi $S$ di động trên đường thẳng $d$ thì $H$ luôn thuộc một đường tròn cố định có bán kính bằng bao nhiêu?
Hướng dẫn giải:
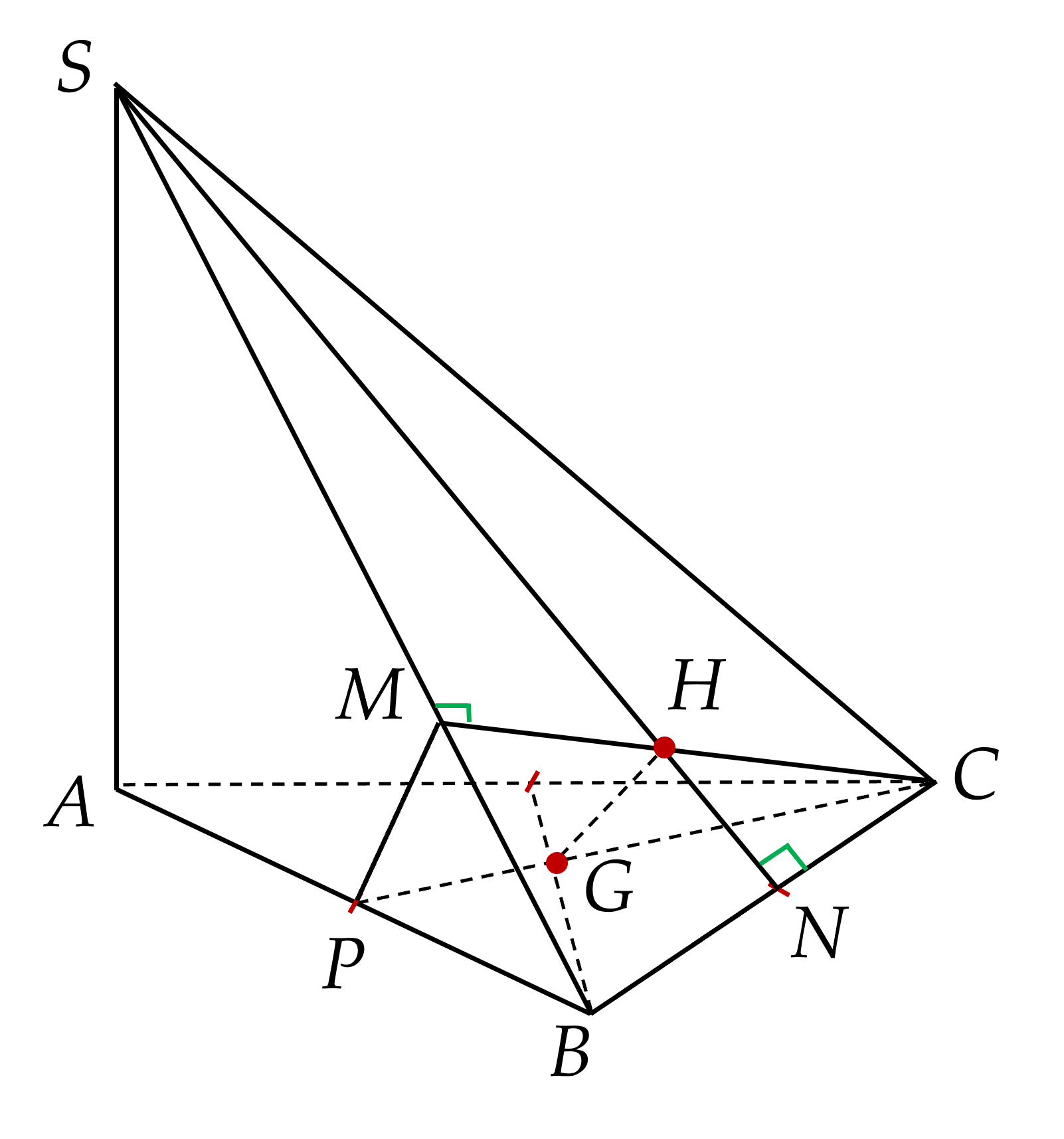
Gọi $G$ là trọng tâm $ABC$ thì $BC\bot \left(SAG \right)\Rightarrow BC\bot GH$. $\left(1 \right)$
Gọi $P,M$ là giao điểm của $\left(CGH \right)$ và $AB,SB$.
Khi đó $CP\bot \left(SAB \right)\Rightarrow CP\bot SB$.
Kết hợp với $SB\bot CM$, suy ra $SB\bot \left(CGH \right)$, dẫn đến $SB\bot GH$. $\left(2 \right)$
Từ $\left(1 \right)$ và $\left(2 \right)$ ta được $GH\bot \left(SBC \right)$, nên $GH\bot HN$.
Suy ra $H$ thuộc đường tròn đường kính $GN=\dfrac{1}{3}.\dfrac{12. \sqrt{3}}{2}=2\sqrt{3}$.
Vậy $H$ thuộc đường tròn có bán kính bằng $\sqrt{3}$.
