Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần trắc nghiệm (7 điểm) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho a là số thực dương và m,n là các số thực tùy ý. Mệnh đề nào sau đây đúng?
Khẳng định nào dưới đây sai?
Cho a là số thực dương. Khi đó ln5a−ln2a bằng
Hàm số nào dưới đây đồng biến trên R?
Tập giá trị của hàm số y=log2x là
Nghiệm của phương trình log3(2x−1)=2 là
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông tại B. Đường thẳng nào dưới đây không vuông góc với BC?
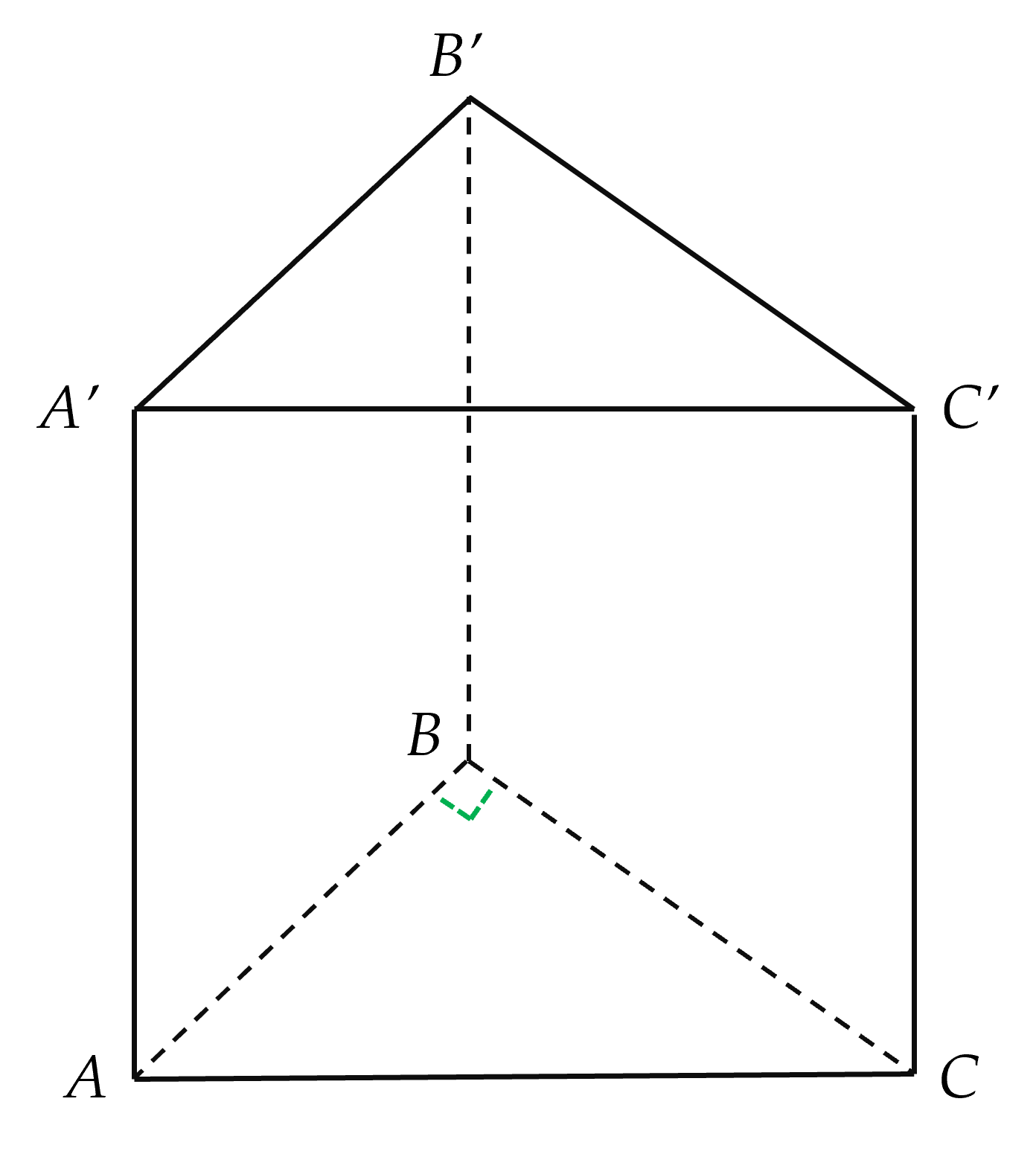
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông tại B. Đường thẳng nào dưới đây vuông góc với (ABB′A′)?

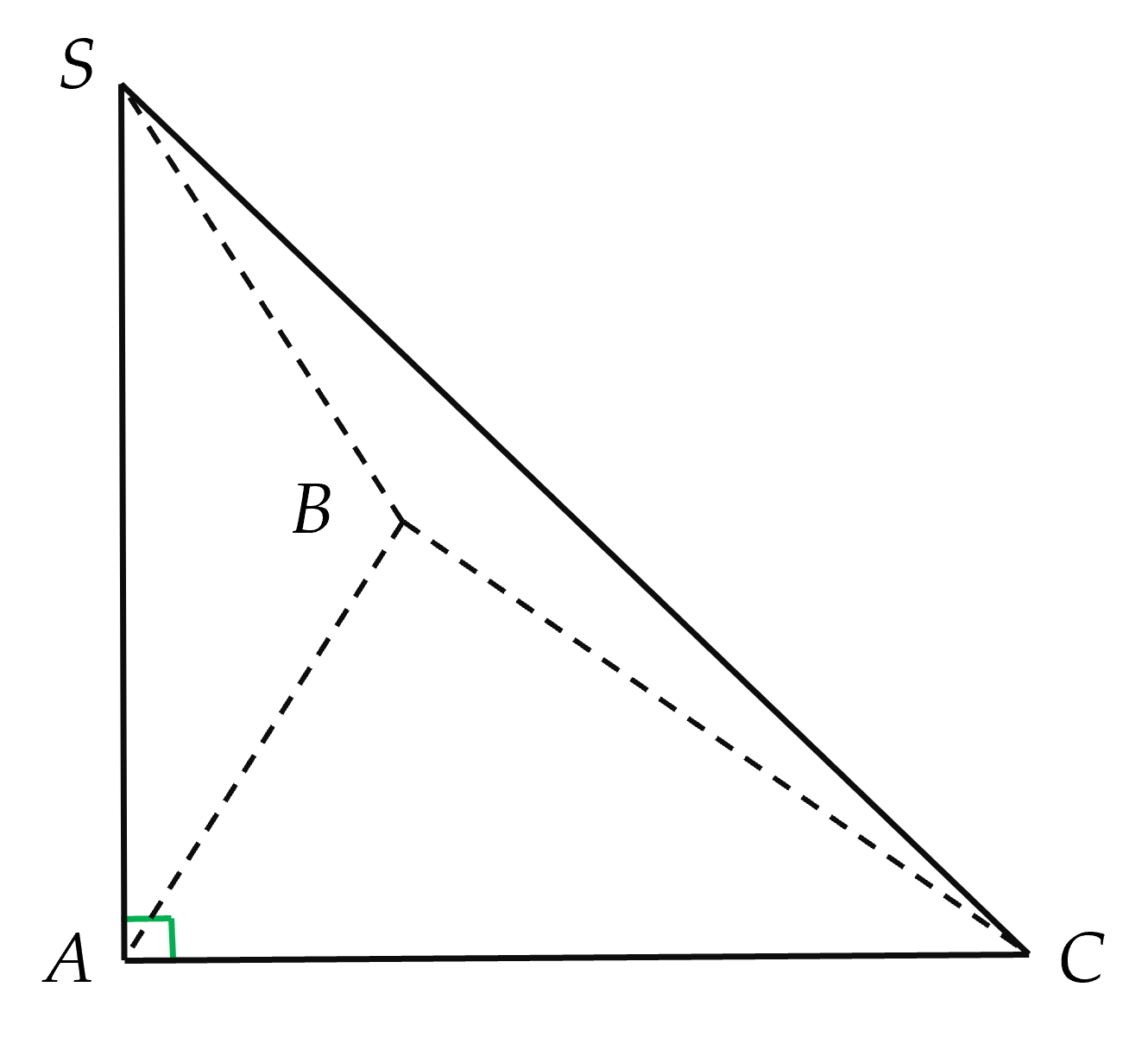
Cho hình chóp tam giác S.ABC có SA vuông góc với đáy. Hai mặt phẳng nào dưới đây vuông góc với nhau?
Trong không gian, cho (P)//(Q), A∈(P) và M∈(Q). Biết rằng AM⊥(Q) và AM=2. Khi đó d((P),(Q)) bằng
Thể tích của hình hộp có diện tích đáy bằng 10 và chiều cao bằng 2 là
Hình chóp cụt đều có các mặt bên là hình gì?
Cho các số thực dương x,y và x=1
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) logxy=logyx1. |
|
| b) Bất phương trình logxy<2 khi y<x2 và x>1. |
|
| c) log2x>log4y⇔x>y. |
|
| d) Phương trình log2(x+3)+log2(x+1)=1 vô nghiệm. |
|
Cho phương trình 2x2−x+8−41−3x=0 có hai nghiệm x1;x2. Tính S=x1+x2.
Trả lời:
Cho hình chóp tam giác S.ABC, đáy là tam giác cân tại B. Gọi M là trung điểm của AC và SM⊥(ABC).
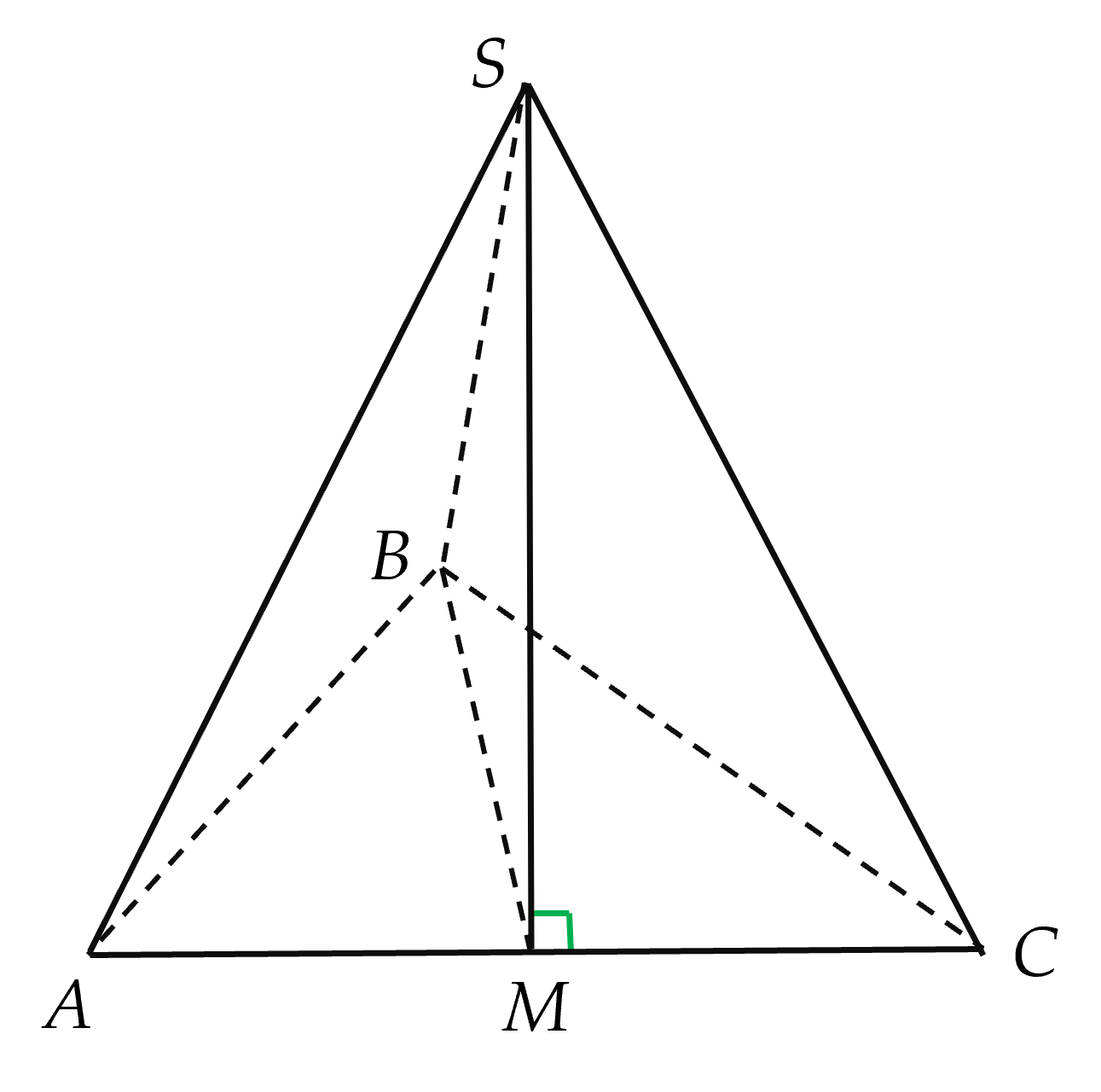
| a) AC⊥(SBM). |
|
| b) d(A,(SBM))=d(C,(SBM)). |
|
| c) Nếu có BC=a3 và AC=2a2 thì d(B,(SAC))=a. |
|
| d) Nếu có SM=a3, BC=a3 và AC=2a2 thì (BS,(SAC))=60∘. |
|
Giá đỡ ba chân ở hình dưới đây đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm. Biết các chân của giá đỡ dài 129 cm, chiều cao của giá đỡ bằng bao nhiêu cm? (làm tròn đến hàng đơn vị)

Trả lời:
Một người gửi 100 triệu đồng vào một ngân hàng với lãi suất 6% / năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 300 triệu bao gồm cả gốc lẫn lãi? (Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền ra).
Trả lời :
Tập nghiệm của bất phương trình log21(x−1)+log2(x−1)+log2(x+3)≥1 có dạng S=(a;+∞). Giá trị của a là
Trả lời:
