Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Ôn tập và kiểm tra cuối chương V SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Giá trị của tham số m để hai mặt phẳng (P):mx+(2m+3)y−2z+5=0 và (Q):x−y+2z−1=0 song song với nhau là
Trong không gian Oxyz, cho mặt phẳng (P):2x−y+3=0. Vectơ nào sau đây không là vectơ pháp tuyến của mặt phẳng (P)?
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1:2x−1=−2y−2=−1z+1, d2:⎩⎨⎧x=ty=0z=−t. Phương trình mặt phẳng (P) chứa đường thẳng d1 tạo với đường thẳng d2 một góc 45∘ là
Trong không gian Oxyz, cho ba điểm A(1;0;1), B(1;1;0) và C(3;4;−1). Đường thẳng đi qua A và song song với BC có phương trình là
Trong không gian với hệ tọa độ Oxyz, mặt cầu (S):(x+2)2+(y+3)2+(z−5)2=36 có tọa độ tâm I là
Trong không gian Oxyz, cho mặt cầu (S):x2+y2+z2+2x−2z−7=0. Bán kính của mặt cầu đã cho là
Trong không gian Oxyz, phương trình mặt phẳng(P) chứa đường thẳng d1:⎩⎨⎧x=1y=1−2tz=1+t và song song với đường thẳng d2:1x−1=2y=2z−1 là
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng song song d1:1x−1=2y+1=3z−2 và d2:3x−4=6y−1=9z−3. Mặt phẳng (P) chứa hai đường thẳng d1 và d2 có phương trình là
Trong không gian Oxyz, cho điểm A(−4;−3;3) và mặt phẳng (P):x+y+z=0. Đường thẳng đi qua A, cắt trục Oz và song song với (P) có phương trình là
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có các đỉnh lần lượt là S(0;0;2a); A(0;0;0); B(a;0;0); C(a;a;0); D(0;2a;0), với a>0.
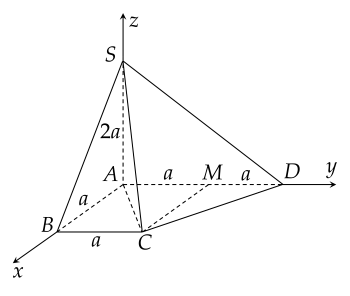
Góc giữa đường thẳng SD và mặt phẳng (SAC) bằng
Cho tam giác ABC có A(2;2;0), B(1;0;2), C(0;4;4). Mặt cầu (S) có tâm A và đi qua trọng tâm G của tam giác ABC có phương trình là
Trong không gian với hệ trục tọa độ Oxyz, phương trình nào dưới đây là phương trình của mặt cầu tâm I(−3;2;−4) và tiếp xúc với mặt phẳng Oxz?
Trong không gian Oxyz, mặt phẳng (P) đi qua hai điểm M(2;0;−1), N(1;−1;3) và vuông góc với mặt phẳng (Q):3x+2y−z+5=0.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) MN=(−1;−1;4). |
|
| b) Một vectơ pháp tuyến của mặt phẳng (Q) là nQ=(3;2−1). |
|
| c) Vectơ pháp tuyến của mặt phẳng (Q) cũng là vectơ pháp tuyến của mặt phẳng (P). |
|
| d) Phương trình mặt phẳng (P):7x−11y−9z+15=0. |
|
Trong hệ trục tọa độ cho các điểm M(0;2;0),N(0;0;−1),P(−1;0;3).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Trọng tâm tam giác MNP là điểm G(0;2;1). |
|
| b) Điểm M thuộc mặt phẳng (α):2x+y−2z=0. |
|
| c) Diện tích tam giác OMN=1. |
|
| d) Tồn tại 2 mặt phẳng (α) qua hai điểm M, N và có khoảng cách từ P đến (α) bằng 2. |
|
Trong không gian Oxyz, cho hai điểm A(1;0;0);B(0;2;0) và các đường thẳng d1:1x+1=−2y=1z−2 ,d2:1x+1=−2y−2=1z+3, Δ:⎩⎨⎧x=2+ty=1+2tz=2+mt.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Vectơ chỉ phương của đường thẳng d1 và d2 lần lượt là ud1=(1;−2;1), ud2=(1;−2;1). |
|
| b) Góc giữa hai đường thẳng d1 và d2 là 60∘. |
|
| c) Có hai giá trị của tham số m thỏa mãn góc giữa đường thẳng Δ và đường thẳng d1 bằng 60∘. |
|
| d) Có hai giá trị của tham số m thỏa mãn góc giữa đường thẳng Δ và đường thẳng AB bằng 45∘. |
|
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục là kilômét), một trạm thu phát sóng điện thoại di động được đặt ở vị trí I(−1;2;5). Biết trạm thu phát sóng đó được thiết kế với bán kính phủ sóng là 4 km.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Phương trình mặt cầu thể hiện phạm vi phủ sóng tối đa của trạm thu phát sóng là x2+y2+z2+2x−4y−10z−14=0. |
|
| b) Điểm A(−1;2;8) nằm ngoài vùng phủ sóng của trạm thu phát sóng điện thoại di động. |
|
| c) Một người đứng ở vị trí có tọa độ điểm B(2;0;−5) sẽ không thu được sóng điện thoại ở trạm phát sóng này. |
|
| d) Nếu hai người cùng bắt được sóng của trạm thu phát sóng điện thoại đó thì khoảng cách tối đa giữa hai người đó là 8 km. |
|
Mặt phẳng (α) đi qua điểm M(2;4;5) và cắt ba tia Ox, Oy, Oz lần lượt tại ba điểm A, B, C sao cho thể tích tứ diện OABC nhỏ nhất có phương trình là ax+by+cz−60=0. Tính a+b+c.
Trả lời:
Trong không gian Oxyz, cho ba điểm A(2;0;0),B(0;1;0),C(0;0;−3). Gọi H là trực tâm tam giác ABC. Độ dài OH có dạng ba (là phân số tối giản có mẫu dương). Tính T=a+b.
Trả lời:
Trên một sườn núi có độ nghiêng đều, người ta trồng một cái cây và giữ cây không bị nghiêng bằng hai sợi dây neo. Giả thiết cây mọc thẳng đứng và trong một hệ tọa độ phù hợp, gốc cây nằm ở điểm O, A và B là điểm buộc dây neo có tọa độ tương ứng là O(0;0;0);A(3;−2;1);B(−5;−3;1) (đơn vị trên mỗi trục tọa độ là mét). Biết rằng hai sợi dây neo đều được buộc vào thân cây tại điểm (0;0;5) và dây kéo căng tạo thành các đoạn thẳng. Tổng các góc tạo bởi mỗi dây neo và mặt phẳng sườn núi bằng bao nhiêu độ? (làm tròn kết quả đến hàng đơn vị của độ)

Trả lời: ∘.
Trong không gian Oxyz, cho hai đường thẳng d1:2x−1=1y+2=−2z−2, d2:−1x−2=1y−3=1z−4 và mặt phẳng (P):x−y+z−2024=0. Gọi Δ là đường thẳng song song với mặt phẳng (P) và cắt d1,d2 lần lượt tại A,B sao cho AB=32. Biết u=(a;b;1) là một vectơ chỉ phương của đường thẳng Δ, khi đó giá trị của biểu thức T=a2024+b2025 bằng bao nhiêu?
Trả lời: .
Trong không gian với hệ tọa độ Oxyz, cho A(−3;1;1), B(1;−1;5) và mặt phẳng (P):2x−y+2z+11=0. Mặt cầu (S) đi qua hai điểm A,B và tiếp xúc với (P) tại điểm C. Biết C luôn thuộc một đường tròn (T) cố định. Tính bán kính r của đường tròn (T).
Trong không gian với hệ toạ độ Oxyz, gọi I(a;b;0) và r lần lượt là tâm và bán kính mặt cầu đi qua A(2;3−3),B(2;−2;2),C(3;3;4). Khi đó, giá trị của T=a+b+r2 bằng bao nhiêu?
Trả lời: .
