Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Những luận điểm cho phần thi toán SVIP
Nội dung này do giáo viên tự biên soạn.
Những luận điểm cho phần thi toán
Mục đích tổng thể của Bài kiểm tra Toán SAT là đánh giá mức độ thông thạo, hiểu biết và khả năng áp dụng các khái niệm, kỹ năng và thực hành toán học của học sinh, những điều kiện tiên quyết nhất và hữu ích cho nhiều chuyên ngành và nghề nghiệp ở trường đại học. Bài kiểm tra Toán SAT sẽ ra các yêu cầu về ít chuyên đề hơn nhưng là những chuyên đề quan trọng hơn so với SAT cũ. Để đạt kết quả cao trong bài thi SAT mới này, học sinh sẽ cần thể hiện khả năng thông thạo các bài tập toán, thông thạo các quy trình toán học và hiểu khái niệm về các ý trong toán học. Cùng với các kiến thức trong sách, đề thi cũng sẽ xuất hiện các bài toán ứng dụng phong phú hơn.
Như với phần Đọc, Viết và Bài luận, một số yếu tố ra đề chính dựa trên kiến thức nền tảng được đan xen vào đề Toán. Các yếu tố như:
» tập trung vào nội dung sát với mục đích đầu vào đại học và nghề nghiệp;
» nhấn mạnh vào giải quyết vấn đề và phân tích dữ liệu; và
» bao gồm cả phần có dùng máy tính bỏ túi (calculator) và không dùng máy tính cũng như chú ý đến việc sử dụng máy tính như một công cụ.
Tập trung vào nội dung trọng tâm nhất (FOCUSING ON CONTENT THAT MATTERS MOST)
Ngày nay, có một sự mất kết nối lớn về toán học giữa hệ thống giáo dục từ mẫu giáo đến lớp 12 và hệ thống giáo dục đại học. Trong một cuộc khảo sát quốc gia gần đây, các giáo viên trung học và giảng viên đại học đã được hỏi liệu học sinh rời trường trung học có chuẩn bị cho môn toán trình độ đại học hay không. Gần 90% giáo viên trung học nói có. Gần 75% giảng viên đại học nói không.
Kết quả của sự mất kết nối này có thể được nhìn thấy ở tỷ lệ học lại kiến thức cơ bản cao phổ biến ở các trường cao đẳng, đại học. Trong các lớp phụ đạo, học sinh thường phải tự trả tiền túi để học những gì lẽ ra phải học trong hệ thống trường học từ mẫu giáo đến lớp 12. Sinh viên trong các lớp phụ đạo cũng thường có tỉ lệ hoàn thành chương trình đại học thấp hơn.
Một trong những cách quan trọng nhất để kỳ thi SAT mới giải quyết khoảng cách giữa mong muốn ở đại học và k–12 là thông qua việc tập trung vào nội dung trọng tâm nhất đối với giáo dục sau trung học.
Các cuộc khảo sát của các khoa ở đại học và các nghiên cứu về nhu cầu của khóa học đầu vào ở đại học đã nhiều lần chỉ ra kết luận rằng các giảng viên đánh giá cao phần nhỏ các yêu cầu tiên quyết hơn là sự tiếp xúc hời hợt với nhiều chủ đề. Các yêu cầu tiên quyết cho phép sinh viên xây dựng dựa trên những gì họ biết và áp dụng kiến thức này để giải quyết các vấn đề thực chất. Như một cuộc khảo sát đã lưu ý:
Bởi vì kết quả khảo sát sau trung học chỉ ra rằng việc tiếp nhận nghiêm túc hơn các kiến thức nội dung và kỹ năng cơ bản cần thiết cho các khóa học đại học sẽ giúp học sinh chuẩn bị tốt hơn cho việc học đại học và công việc sau này, các tiểu bang có thể kiểm tra các tiêu chuẩn và, nếu cần, giảm bớt chúng, chỉ tập trung vào kiến thức và kỹ năng mà nghiên cứu cho thấy là cần thiết để sẵn sàng vào đại học và nghề nghiệp cũng như thành công sau trung học. [1]
Gần đây, trong một cuộc khảo sát quốc gia được công bố vào năm 2011 bởi David Conley và các đồng nghiệp của ông, hơn 1.800 giảng viên sau trung học từ nhiều lĩnh vực nội dung và loại hình tổ chức đã đánh giá tầm quan trọng của từng nội dung trong Các tiêu chuẩn cốt lõi chung của tiểu bang về toán học ở bậc trung học (the Common Core State Standards for Mathematics CCSSMM, giống như Khung chương trình giáo dục phổ thông của Việt Nam). Kết quả của cuộc khảo sát này củng cố kết luận rằng một số lĩnh vực nội dung cần được nhấn mạnh hơn nhiều so với những nội dung khác. Tầm quan trọng đặc biệt của đại số là không thể nhầm lẫn dựa trên dữ liệu của Conley, như thể hiện trong hình bên dưới. Các lĩnh vực toán học khác có kết quả khảo sát không tập trung, thường bao gồm nhiều nội dung không liên quan đến hầu hết các yêu cầu ở đại học và/hoặc không phải là điều kiện tiên quyết cho hầu hết các môn học ở đại học. Dữ liệu từ nghiên cứu này hỗ trợ trực tiếp việc lựa chọn nội dung được thể hiện trong SAT mới.
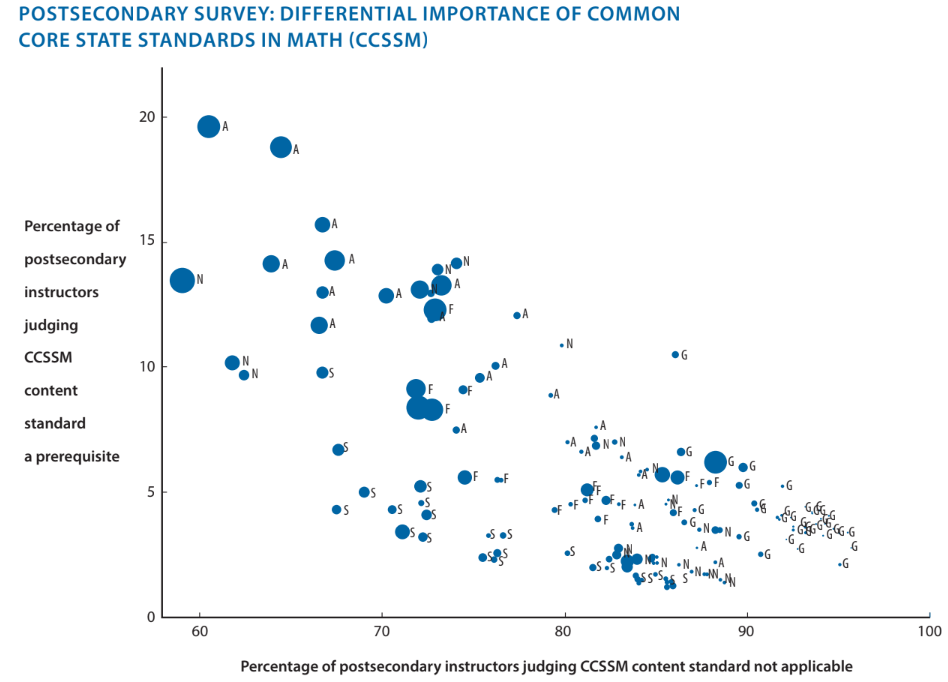
Trục tung biểu thị tỷ lệ phần trăm giảng viên sau trung học đánh giá tầm quan trọng của các nội dung trong CCSSM như một điều kiện tiên quyết cho các khóa học đại học giới thiệu. Hình tròn lớn hơn thể hiện tầm quan trọng hơn, hình tròn nhỏ hơn thể hiện ít quan trọng hơn.
Chú thích: N = Số học; A = Đại số; F = Hàm số; G = Hình học; S = Thống kê và Xác suất.
Vào tháng 10 năm 2013, the Council of Chief State School Officers đã công bố các nguyên tắc đánh giá tổng hợp cho phần đánh giá Ngữ văn-Tiếng Anh (ELA/literacy) và toán học gắn với các tiêu chuẩn đại học và nghề nghiệp. Những nguyên tắc đánh giá này nhằm tạo cơ sở cho sự xem xét của các bang về hệ thống đánh giá của họ. Các nguyên tắc nhấn mạnh tầm quan trọng vào việc tập trung đánh giá những gì trọng tâm nhất. Nguyên tắc gắn kết đầu tiên trong toán học là “tập trung nhiều vào nội dung cần thiết nhất để thành công trong toán học sau này.” Như tài liệu lưu ý, “Trong hệ thống đánh giá gắn kết giữa trường trung học và với đại học và nghề nghiệp, trường trung học tập trung vào các nội dung có khả năng áp dụng rộng rãi cho nghề nghiệp và giáo dục sau trung học.” [3] Kì thi SAT mới tuân theo nguyên tắc này.
Giải quyết vấn đề và phân tích dữ liệu (PROBLEM SOLVING AND DATA ANALYSIS)
Có đủ bằng chứng cho thấy việc giải quyết vấn đề và phân tích dữ liệu — khả năng trình bày một vấn đề, xem xét các yếu tố liên quan, chú ý đến ý nghĩa của các đại lượng, biết và sử dụng các thuộc tính khác nhau của các phép toán và đối tượng — rất quan trọng đối với trường đại học, công việc, và cuộc sống. Tuy nhiên, kết quả kỳ thi Chương trình Đánh giá Sinh viên Quốc tế (PISA) của Mỹ, trong đó bao gồm một bài kiểm tra kiến thức toán học, cho thấy rằng các trường học của chúng ta không làm tốt trong việc đào tạo những sinh viên có trình độ đọc hiểu về định lượng. Việc đọc hiểu định lượng (tư duy định lượng) tốt là một phần của việc tham gia vào một nền dân chủ; nó rất quan trọng đối với các nhà tuyển dụng-những người cần nhân viên có thể sử dụng toán học bên ngoài lớp học; và nó quan trọng không chỉ đối với các lĩnh vực khoa học, công nghệ, kỹ thuật và toán học (STEM) mà còn đối với nhiều chuyên ngành đại học.
Một nghiên cứu gần đây của Trung tâm Giáo dục và Kinh tế Quốc gia cũng hỗ trợ cho việc nhấn mạnh vào việc giải quyết vấn đề và phân tích dữ liệu trong SAT, nó phân tích nhu cầu toán học thực tế của chương trình khóa học và bài tập trong các trường học hai năm. Nghiên cứu cho thấy rằng sinh viên theo học các chương trình đào tạo đại học hai năm phải có khả năng giải các bài toán nhiều bước liên quan đến tỷ lệ, mối quan hệ tỷ lệ, tỷ lệ phần trăm, chuyển đổi đơn vị và các bài toán đo lường phức tạp. [4]
Những vấn đề như vậy là một điểm kết nối lý tưởng cho khoa học và cho sự sẵn sàng cho đại học và nghề nghiệp vì rất nhiều đại lượng trong khoa học ứng dụng liên quan đến các mối quan hệ tỷ lệ và/hoặc được hình thành bằng phép chia (chẳng hạn như tỷ lệ, mật độ và độ dốc). Do đó, phần lớn khoa học ứng dụng cơ bản là tư duy theo tỷ lệ và kết hợp tỷ lệ. Hãy thử tính đến bài toán: học sinh sử dụng dữ liệu tham khảo để xác định chi phí năng lượng của các loại nhiên liệu khác nhau, dựa trên các mối quan hệ tỷ lệ, chuyển đổi đơn vị và các kỹ năng khác. Các bối cảnh thực tế, liên quan đến nghề nghiệp, chẳng hạn như bản vẽ tỷ lệ của cơ khí động cơ diesel và ước tính xây dựng, dày đặc với tỷ lệ đơn vị, mối quan hệ tỷ lệ, tỷ lệ phần trăm, v.v.
Phần Giải quyết vấn đề và Phân tích dữ liệu của bài thi SAT mới chứa nhiều bài toán của nhiều phần. Những bài toán này cho phép học sinh khám phá một tình huống phong phú hơn và đọ dài lớn hơn so với các bài toán trong bài SAT cũ. Đổi lại, điều đó cho phép SAT mới kết hợp tốt hơn mô hình toán học và các thực hành toán học khác. Đặc trưng này của bài thi mới cũng phản ánh cấu trúc của kỳ thi PISA, được tổ chức theo tập hợp, mỗi tập hợp bao gồm một số mục.
Phần dùng máy tính và không máy tính (CALCULATOR AND NO-CALCULATOR PORTIONS)
Các dữ liệu rõ ràng cho thấy rằng các giảng viên đại học kỳ vọng sinh viên thông thạo phần số học hữu tỷ. Phần thi không có máy tính trong bài thi SAT mới sẽ giúp đảm bảo với những giảng viên rằng những học sinh đạt điểm cao trong bài thi SAT không thiếu các điều kiện tiên quyết cơ bản.
Máy tính bỏ túi là một công cụ và các quyết định về việc khi nào sử dụng và không sử dụng nó với một vài cân nhắc. Ví dụ, hãy xem xét một bài toán trong đó mục tiêu chính là chọn một mô hình toán học cho một tình huống phức tạp, thực hiện một số tính toán với mô hình, sau đó liên hệ kết quả của các tính toán này với tình huống ban đầu. Một mặt, việc sử dụng máy tính cho phép học sinh tập trung vào tính hiệu quả của mô hình và đánh giá các kết luận của nó. Mặt khác, việc giải quyết bài toán và phân tích dữ liệu tốt là rất quan trọng để kiểm soát các phép tính và sự hiểu biết chắc chắn về cấu trúc đại số sẽ giúp học sinh có những lựa chọn khôn ngoan trong việc tiến hành các bước trong một bài toán. Học sinh có thể phụ thuộc quá nhiều vào khả năng tính toán của máy tính mà không chú ý đến các lập luận định lượng và trừu tượng, cái mà làm nền tảng cho toán học. Ngược lại, các học sinh cũng có thể bị hạn chế trong các phép tính số và đại số mà công nghệ có thể xử lý tốt.
Các câu hỏi trong phần máy tính của bài thi được thiết kế để đánh giá khả năng của học sinh trong việc đưa ra những lựa chọn khôn ngoan giữa hai thái cực. Đối với một số câu hỏi, máy tính sẽ cho ra kết quả hiệu quả; đối với những câu hỏi khác, khả năng sử dụng cấu trúc hoặc suy luận trừu tượng sẽ dẫn đến giải pháp nhanh nhất. Phần máy tính chứa cả hai loại câu hỏi; đáng chú ý là không phải tất cả các câu hỏi trong phần này sẽ được giải tốt nhất bằng máy tính bỏ túi.
TÀI LIỆU TRÍCH DẪN
[1] David T. Conley, Understanding University Success (Eugene, OR: Center for Educational Policy Research, University of Oregon, 2003), http://eric.ed.gov/?id=ED476300; ACT, National Curriculum Survey 2009, 43.
[2] Informed by postsecondary survey data in Conley et al., Reaching the Goal: The Applicability and Importance of the Common Core State Standards to College and Career Readiness (Eugene, OR: Educational Policy Improvement Center, 2011), http://www.epiconline.org/publications/document-detail.dot?id=09535d00466a-498f-ac44-98f4c372d9c1.
[3] Council of Chief State School Officers, States’ Commitment to High-Quality Assessments Aligned to College- and Career-Readiness (Washington, DC: Council of Chief State School Officers, 2013), http://www.ccsso.org/documents/2013/CCSSO%20Assessment%20Quality%20Principles%2010-1-13%20FINAL.pdf.
[4] National Center on Education and the Economy, What Does It Really Mean to Be College and Work Ready? The Mathematics Required of First Year Community College Students (Washington, DC: National Center on Education and the Economy, 2013), 2, http://www.ncee.org/wp-content/uploads/2013/05/NCEE_MathReport_May20131.pdf.
Bạn có thể đăng câu hỏi về bài học này ở đây
