Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Dấu của tam thức bậc hai SVIP
1. Định lý về dấu của tam thức bậc hai
a. Tam thức bậc hai
Tam thức bậc hai đối với $x$ là biểu thức có dạng $f(x)=ax^2+bx+c$, trong đó $a,b,c$ là những hệ số, \(a\ne0\).
Ví dụ: $-5x^2+6x-1$ là một tam thức bậc hai; $3x-4$ không phải là một tam thức bậc hai.
b. Dấu của tam thức bậc hai
Định lý về dấu tam thức bậc hai:
Cho $f(x)=ax^2+bx+c$, \(a\ne0\), \(\Delta=b^2-4ac\).
+) Nếu \(\Delta< 0\) thì $f(x)$ luôn cùng dấu với hệ số $a$, với mọi \(x\inℝ\).
+) Nếu \(\Delta=0\) thì $f(x)$ luôn cùng dấu với hệ số $a$, trừ khi \(x=\dfrac{-b}{2a}\)
+) Nếu \(\Delta>0\) thì $f(x)$ luôn cùng dấu với hệ số $a$ khi $x<x_1$ hoặc $x>x_2$, trái dấu với hệ số $a$ khi $x_1<x<x_2$, trong đó $x_1, x_2 (x_1<x_2)$ là hai nghiệm của $f(x)$.
Chú ý: Trong định lý trên, có thể thay biệt thức \(\Delta=b^2-4ac\) bằng biệt thức thu gọn \(\Delta'=\left(b'\right)^2-4ac\).
Minh họa hình học: Định lý về dấu của tam thức bậc hai có hình minh họa hình học sau:
| \(\Delta< 0\) | \(\Delta=0\) | \(\Delta>0\) | |
| \(a>0\) |  |
 |
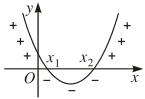 |
| \(a< 0\) |  |
 |
 |
c. Áp dụng
Ví dụ: Xét dấu tam thức $f(x)=-x^2+3x-5$.
Lời giải: $f(x)$ có \(\Delta=-11< 0\), hệ số $a=-1<0$ nên $f(x)<0$ với mọi $x$.
Ví dụ: Lập bảng xét dấu tam thức $f(x)=2x^2-5x+2$.
Lời giải: $f(x)=2x^2-5x+2$ có hai nghiệm phân biệt $x_1=\dfrac{1}{2}, x_2=2$, hệ số $a=2>0$.
Ta có bảng xét dấu $fx)$ như sau:
| $x$ | $-\infty$ | $\dfrac{1}{2}$ | $2$ | $+\infty$ | |||
| $f(x)$ | $+$ | $0$ | $-$ | $0$ | $+$ |
Ví dụ: Xét dấu biểu thức:
\(f\left(x\right)=\dfrac{2x^2-x-1}{x^2-4}\)
Lời giải:
Xem video này để hiểu rõ hơn cách xét dấu biểu thức trên.
Xét dấu các tam thức $2x^2-x-1$ và $x^2-4$ rồi lập bảng xét dấu $f(x)$ ta được:
| $x$ | $-\infty$ | $-2$ | $-\dfrac{1}{2}$ | $1$ | $2$ | $+\infty$ | |||||
| $2x^2-x-1$ | $+$ | \(\Big|\) | $+$ | $0$ | $-$ | $0$ | $+$ | \(\Big|\) | $+$ | ||
| $x^2-4$ | $+$ | $0$ | $-$ | \(\Big|\) | $-$ | \(\Big|\) | $-$ | $0$ | $+$ | ||
| $f(x)$ | $+$ | || | $-$ | $0$ | $+$ | $0$ | $-$ | || | $+$ |
2. Bất phương trình bậc hai một ẩn
a. Bất phương trình bậc hai
Bất phương trình bậc hai ẩn $x$ là bất phương trình dạng $ax^2+bx+c<0$ (hoặc $ax^2+bx+c \leq 0$; $ax^2+bx+c>0$, $ax^2+bx+c \geq 0$), trong đó $a,b,c$ là những số thực đã cho, \(a\ne0\).
Ví dụ:
$\dfrac{1}{8}x^2-16x-17<0$, $-5x^2+6x-1>0$; $-4x^2+16x+18 \leq 0$ và $-9x^2+14x+5 \geq 0$ là những bất phương trình bậc hai ẩn $x$.
b. Giải bất phương trình bậc hai
Xem video này để hiểu rõ hơn cách giải bất phương trình bậc hai.
Giải bất phương trình bậc hai $ax^2+bx+c <0$ thực chất là tìm các khoảng mà trong đó $f(x)=ax^2+bx+c$ cùng dấu với hệ số $a$ (trường hợp $a<0$) hay trái dấu với hệ số $a$ (trường hợp $a>0$)
Ví dụ: Tìm các giá trị của tham số $m$ để phương trình sau có hai nghiệm trái dấu:
$2x^2-(m^2-m+1)x+2m^2-3m-5=0$.
Lời giải:
Phương trình bậc hai sẽ có hai nghiệm trái dấu khi và chỉ khi các hệ số $a$ và $c$ trái dấu, tức là $m$ phải thỏa mãn điều kiện
$2(2m^2-3m-5)<0$ \(\Leftrightarrow\) $2m^2-3m-5<0$.
Vì tam thức $f(m)=2m^2-3m-5$ có hai nghiệm là $m_1=-1$; $m_2=\dfrac{5}{2}$ và hệ số của $m^2$ dương nên
$2m^2-3m-5<0$ \(\Leftrightarrow\) $-1<m<\dfrac{5}{2}$.
Bạn có thể đăng câu hỏi về bài học này ở đây
