Bài học cùng chủ đề
- Phương trình đường tròn. Phương trình tiếp tuyến của đường tròn
- Phương trình đường tròn đi qua ba điểm, phương trình tiếp tuyến của đường tròn
- Phương trình đường tròn
- Tìm tâm và bán kính dựa vào phương trình đường tròn
- Lập phương trình đường tròn (Phần 1)
- Lập phương trình đường tròn (Phần 2)
- Điều kiện để phương trình là phương trình đường tròn
- Phương trình tiếp tuyến của đường tròn
- Luyện tập tổng hợp
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phương trình đường tròn. Phương trình tiếp tuyến của đường tròn SVIP
1. Phương trình đường tròn
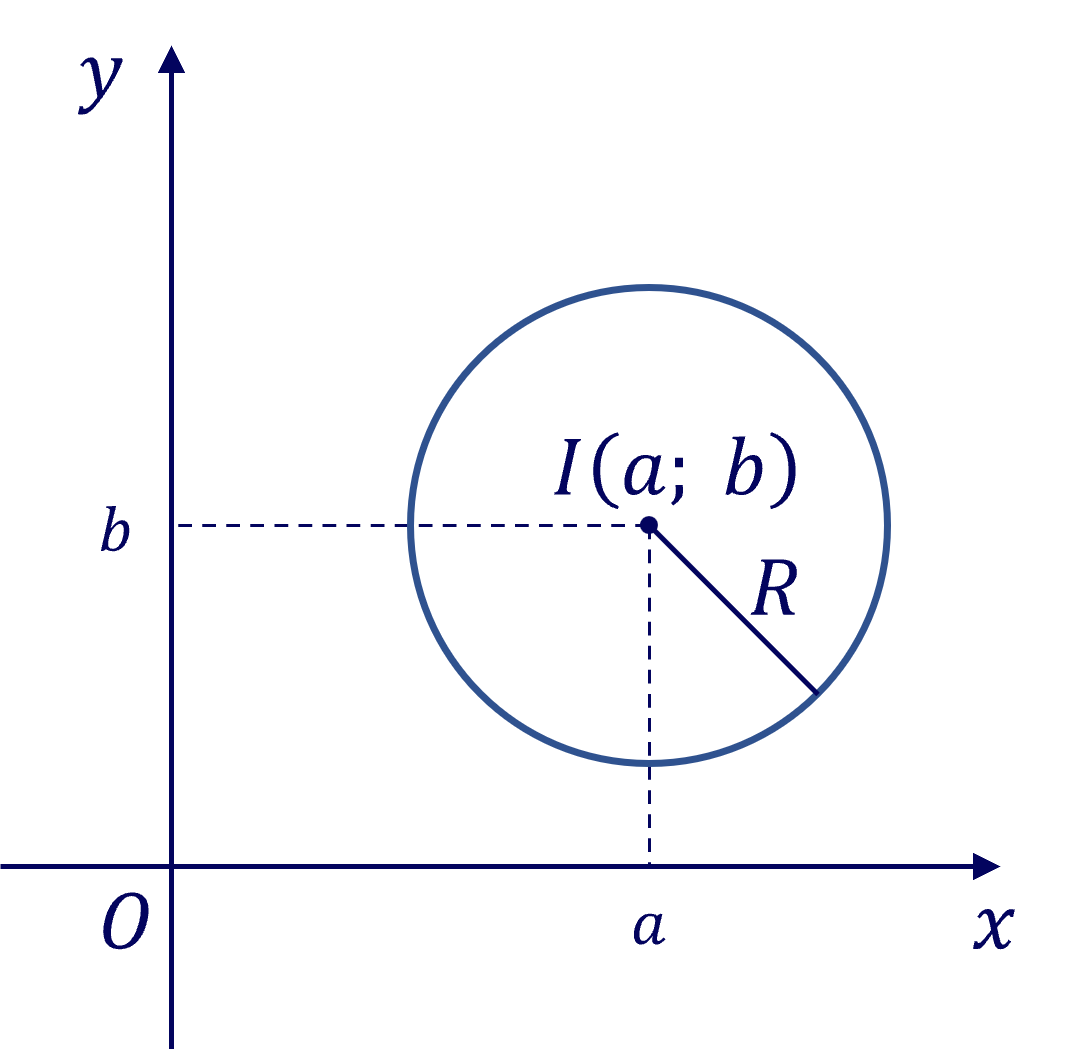
Phương trình \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) phương trình đường tròn tâm \(I\left(a;b\right)\) bán kính \(R\).
Nhận xét: Ta có
\(\left(x-a\right)^2+\left(y-b\right)^2=R^2\)
\(\Leftrightarrow x^2+y^2-2ax-2by+\left(a^2+b^2-R^2\right)=0\).
Vậy phương trình đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) có thể được viết dưới dạng \(x^2+y^2-2ax-2by+c=0\), trong đó \(c=a^2+b^2-R^2\).
Ngược lại, phương trình \(x^2+y^2-2ax-2by+c=0\) là phương trình của đường tròn \(\left(C\right)\) khi và chỉ khi \(a^2+b^2-c>0\). Khi đó đường tròn \(\left(C\right)\) có tâm \(I\left(a;b\right)\) và bán kính \(R=\sqrt{a^2+b^2-c}\).
Ví dụ 1: Tìm tâm và bán kính của đường tròn trong mỗi trường hợp sau:
a) Đường tròn có phương trình \(\left(x+2\right)^2+\left(y-3\right)^2=25\);
b) Đường tròn có phương trình \(x^2+4x+y^2-6y-12=0\).
Giải
a) Ta có \(\left(x+2\right)^2+\left(y-3\right)^2=25\Leftrightarrow\left[x-\left(-2\right)\right]^2+\left(y-3\right)^2=5^2\).
Suy ra đường tròn có tâm \(I\left(-2;3\right)\) và bán kính \(R=5\).
b) Ta có \(x^2+4x+y^2-6y-12=0\Leftrightarrow x^2+y^2-2.\left(-2\right)x-2.3y-12=0\) và \(\left(-2\right)^2+3^2+12=25>0\)
suy ra đường tròn có tâm \(I\left(-2;3\right)\) và bán kính \(R=\sqrt{25}=5\).
Ví dụ 2: Viết phương trình đường tròn trong mỗi trường hợp sau:
a) Có tâm \(I\left(-2;3\right)\) và đi qua \(A\left(2;0\right)\);
b) Có tâm \(I\left(1;-2\right)\) và tiếp xúc với đường thẳng \(\Delta:3x-4y+14=0\).
Giải
a) Vì đường tròn có tâm \(I\) và đi qua \(A\) nên có bán kính là
\(R=IA=\left|\overrightarrow{IA}\right|=\sqrt{\left(2+2\right)^2+\left(0-3\right)^2}=5\).
Vậy phương trình đường tròn là
\(\left[x-\left(-2\right)\right]^2+\left(y-3\right)^2=5^2\Leftrightarrow\left(x+2\right)^2+\left(y-3\right)^2=25\).
b) Vì đường tròn có tâm \(I\) và tiếp xúc với đường thẳng \(\Delta\) nên bán kính \(R\) của đường tròn bằng khoảng cách từ điểm \(I\) đến đường thẳng \(\Delta\).
\(R=d\left(I,\Delta\right)=\dfrac{\left|3.1-4\left(-2\right)+14\right|}{\sqrt{3^2+4^2}}=5\).
Vậy phương trình đường tròn là
\(\left(x-1\right)^2+\left[y-\left(-2\right)\right]^2=5^2\Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2=25\).
Ví dụ 3: Viết phương trình đường tròn \(\left(C\right)\) đi qua ba điểm \(A\left(2;6\right)\), \(B\left(-6;2\right)\), \(C\left(-1;-3\right)\).
Giải
Cách 1:
Phương trình đường tròn \(\left(C\right)\) có dạng \(x^2+y^2-2ax-2by+c=0\).
Vì \(A\left(2;6\right)\in\left(C\right)\) nên ta có \(2^2+6^2-2a.2-2b.6+c=0\Leftrightarrow4a+12b-c=0\) (1).
Tương tự, thay tọa độ các điểm \(B\), \(C\) vào phương trình \(\left(C\right)\) ta được hai phương trình
\(12a-4b+c=-40\). (2)
\(2a+6b+c=-10\). (3)
Cộng theo từng vế phương trình (1) với phương trình (2), phương trình (1) với phương trình (3), ta được hệ phương trình
\(\left\{{}\begin{matrix}16a+8b=0\\6a+18b=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=2.\end{matrix}\right.\)
Suy ra \(c=4a+12b-40=-20\).
Vậy phương trình đường tròn \(\left(C\right)\) là \(x^2+y^2+2x-4y-20=0\).
Cách 2:
Giả sử tâm của đường tròn là điểm \(I\left(a;b\right)\). Ta có \(IA=IB=IC\Leftrightarrow IA^2=IB^2=IC^2\).
Vì \(IA^2=IB^2\), \(IB^2=IC^2\)nên
\(\left\{{}\begin{matrix}\left(2-a\right)^2+\left(6-b\right)^2=\left(-6-a\right)^2+\left(2-b\right)^2\\\left(-6-a\right)^2+\left(2-b\right)^2=\left(-1-a\right)^2+\left(-3-b\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2-4a+4+b^2-12b+36=a^2+12a+36+b^2-4b+4\\a^2+12a+36+b^2-4b+4=a^2+2a+1+b^2+6b+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-16a-8b=0\\10a-10b=-30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=2.\end{matrix}\right.\)
Bán kính đường tròn \(\left(C\right)\) là
\(R=IA=\sqrt{\left[2-\left(-1\right)\right]^2+\left(6-2\right)^2}=5\).
Phương trình đường tròn \(\left(C\right)\) là
\(\left[x-\left(-1\right)\right]^2+\left(y-2\right)^2=5^2\Leftrightarrow\left(x+1\right)^2+\left(y-2\right)^2=25\).
Cách 3:
Các đoạn thẳng \(AB\), \(AC\) tương ứng có các trung điểm là \(M\left(-2;4\right)\), \(N\left(\dfrac{1}{2};\dfrac{3}{2}\right)\).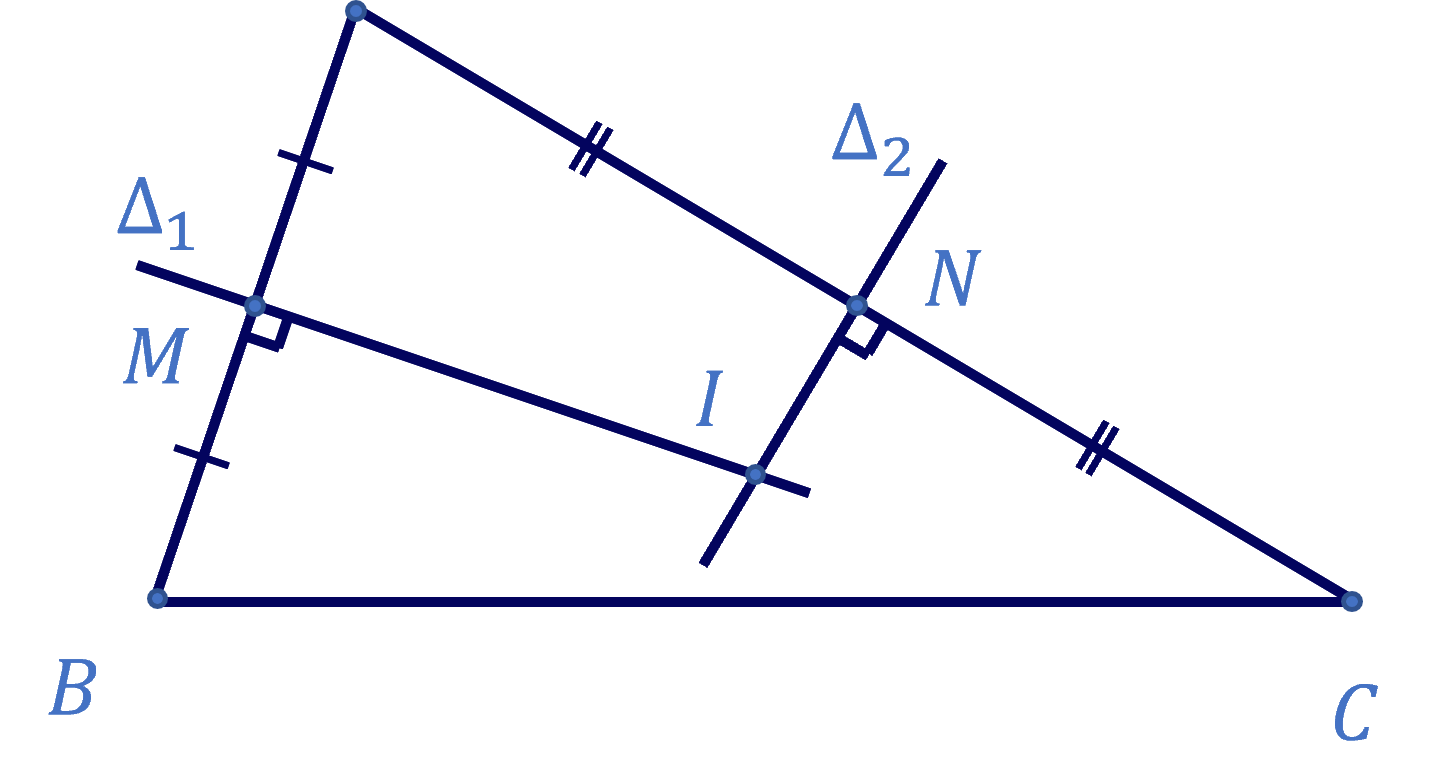
Đường trung trực \(\Delta_1\) của đoạn thẳng \(AB\) đi qua \(M\left(-2;4\right)\) và có vectơ pháp tuyến \(\overrightarrow{AB}=\left(-8;-4\right)\).
Vì \(\overrightarrow{AB}\left(-8;-4\right)\) cùng phương với \(\overrightarrow{n_1}\left(2;1\right)\) nên \(\Delta_1\) cũng nhận \(\overrightarrow{n_1}\left(2;1\right)\) là vectơ pháp tuyến.
Do đó, phương trình của đường thẳng \(\Delta_1\) là
\(2\left(x+2\right)+1\left(y-4\right)=0\) hay \(2x+y=0\).
Đường trung trực \(\Delta_2\) của đoạn thẳng \(AC\) đi qua \(N\left(\dfrac{1}{2};\dfrac{3}{2}\right)\) và có vectơ pháp tuyến \(\overrightarrow{AC}=\left(-3;-9\right)\).
Vì \(\overrightarrow{AC}\left(-3;-9\right)\) cùng phương với \(\overrightarrow{n_2}\left(1;3\right)\) nên \(\Delta_2\) cũng nhận \(\overrightarrow{n_2}\left(1;3\right)\) là vectơ pháp tuyến.
Do đó, phương trình của đường thẳng \(\Delta_2\) là
\(1\left(x-\dfrac{1}{2}\right)+3\left(y-\dfrac{3}{2}\right)=0\Leftrightarrow x+3y-5=0\).
Tâm \(I\) của đường tròn \(\left(C\right)\) là giao điểm của hai đường thẳng \(\Delta_1\) và \(\Delta_2\).
Vậy tọa độ của \(I\) là nghiệm của hệ phương trình
\(\left\{{}\begin{matrix}2x+y=0\\x+3y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2.\end{matrix}\right.\)
Suy ra \(I\left(-1;2\right)\). Đường tròn \(\left(C\right)\) có bán kính là \(IA\).
\(IA=\left|\overrightarrow{IA}\right|=\sqrt{\left(-1-2\right)^2+\left(2-6\right)^2}=5\).
Vậy phương trình của \(\left(C\right)\) là \(\left(x+1\right)^2+\left(y-2\right)^2=25\).
2. Phương trình tiếp tuyến của đường tròn
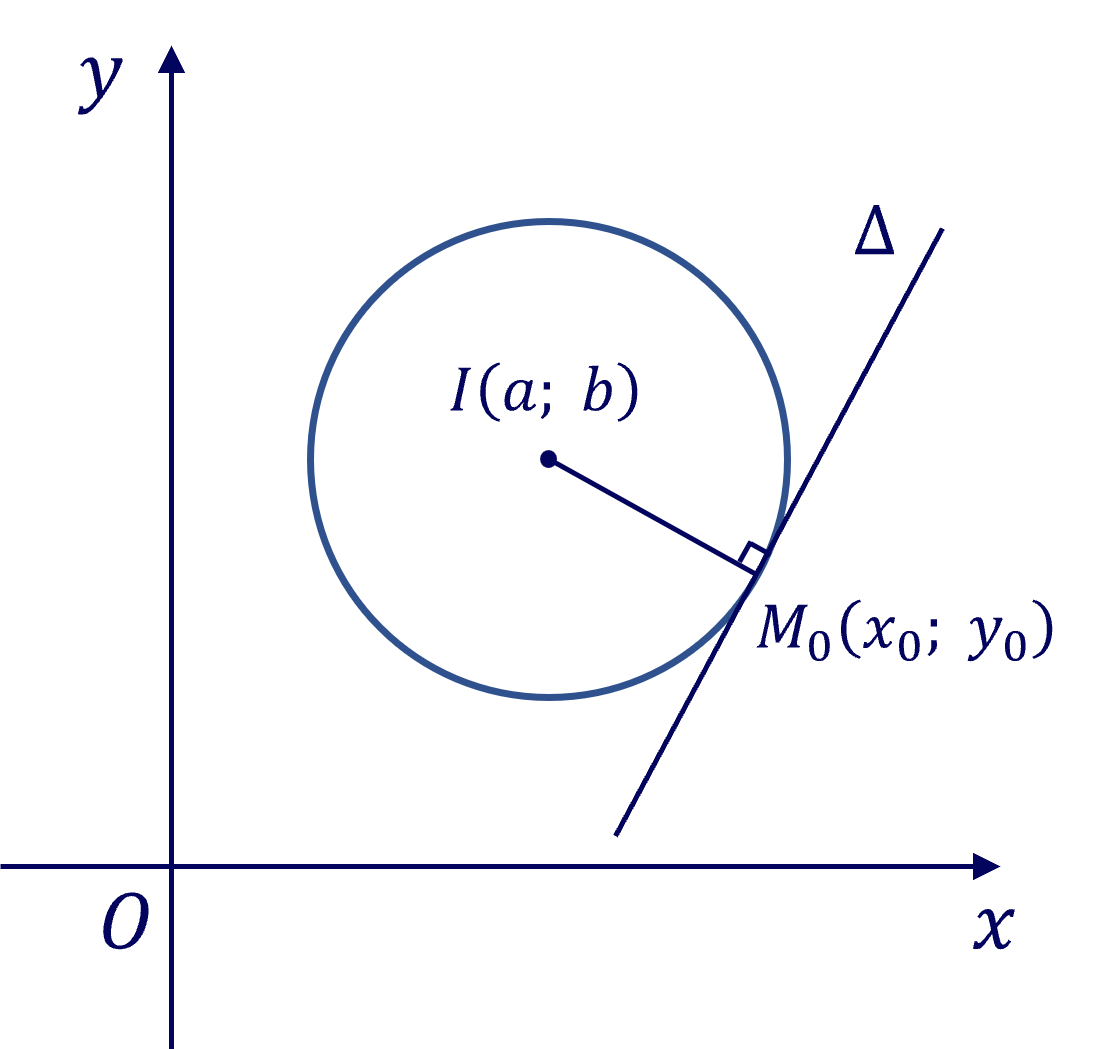
Phương trình tiếp tuyến của đường tròn tâm \(I\left(a;b\right)\) tại điểm \(M_0\left(x_0;y_0\right)\) nằm trên đường tròn là:
\(\left(a-x_0\right)\left(x-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)=0\).
Ví dụ: Viết phương trình tiếp tuyến của đường tròn \(\left(C\right):x^2+y^2+2x-4y-20=0\).
Giải
Đường tròn \(\left(C\right)\) có tâm \(I\left(-1;2\right)\), bán kính \(R=\sqrt{\left(-1\right)^2+2^2+20}=5\).
Tiếp tuyến \(\Delta\) của \(\left(C\right)\) vuông góc với đường thẳng \(IM\), do đó có vectơ pháp tuyến là
\(\overrightarrow{n_{\Delta}}=\overrightarrow{IM}=\left(3-\left(-1\right);5-2\right)=\left(4;3\right)\).
Đường thẳng \(\Delta\) có vectơ pháp tuyến \(\overrightarrow{n_{\Delta}}=\left(4;3\right)\) và đi qua điểm \(M\left(3;5\right)\) nên có phương trình
\(4\left(x-3\right)+3\left(y-5\right)=0\Leftrightarrow4x+3y-27=0\).
Bạn có thể đăng câu hỏi về bài học này ở đây