Đối xứng tâm SVIP

Khẳng định nào dưới đây là đúng?

Khẳng định nào dưới đây là không đúng?

Hai tam giác dưới đây có đối xứng nhau qua điểm O không?

Các câu dưới đây đúng hay sai?

Khẳng định nào dưới đây đúng?

Những hình nào sau đây không có tâm đối xứng?

(Biển cấm đi ngược chiều)

(Biển báo hiệu đường giao nhau)

(Tam giác đều ABC)

(Biển cấm người đi bộ)

(Đoạn thẳng AB)

Bài toán:

Ở hình vẽ bên, ABCD là hình bình hành. Chứng minh rằng M đối xứng với N qua C.

Sắp xếp các dòng sau theo thứ tự hợp lý để được lời giải bài toán trên.

Do đó M đối xứng với N qua C. Từ (1) và (2) suy ra M, C, N thẳng hàng và CM = CN. Chứng minh tương tự, CN // BD, CN = BD. (2) Tứ giác BMCD có BM // CD, BM = CD nên là hình bình hành. Suy ra CM // BD, CM = BD. (1)

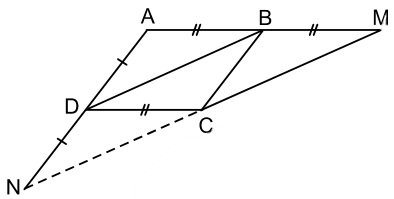Cho bài toán:

Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với C qua N. Chứng minh rằng điểm D đối xứng với điểm E qua A.

Sắp xếp các dòng sau theo thứ tự hợp lý để được lời giải bài toán trên.

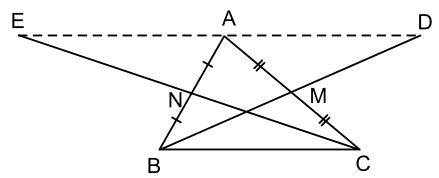
• Từ (1) và (2) suy ra D, A, E thẳng hàng và AD = AE. Do đó D đối xứng với E qua A.
• Chứng minh tương tự, ACBE là hình bình hành nên AE = BC và AE // BC (2)
• Ta có MA = MC, MB = MD, do đó tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường nên là hình bình hành.
• Suy ra AD // BC và AD = BC (1)

Cho bài toán:

Cho tam giác ABC vuông tại A, điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, gọi F là điểm đối xứng với D qua AC. Chứng minh rằng các điểm E và F đối xứng với nhau qua điểm A.

Sắp xếp các dòng sau theo thứ tự hợp lý để được lời giải bài toán trên.

• Chứng minh tương tự, AF = AD và $\widehat{\text{A}_3}=\widehat{\text{A}_4}$.
• Do đó, A là trung điểm của EF hay E và F đối xứng với nhau qua A.
• Suy ra AE = AF (cùng bằng AD) và $\widehat{\text{DAE}}+\widehat{\text{DAF}}=2\left(\widehat{\text{A}_1}+\widehat{\text{A}_3}\right)=180^\circ.$
• Vì $\Delta$ADE có AB là đường trung trực của DE nên là tam giác cân. Do đó AB cũng là đường phân giác, suy ra AE = AD và $\widehat{\text{A}_1}=\widehat{\text{A}_2}$.