Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Làm tròn và ước lượng SVIP
I. LÀM TRÒN SỐ
1. Làm tròn số
Ở nhiều tình huống thực tiễn, ta cần tìm một số thực khác xấp xỉ với số thực đã cho để thuận tiện hơn trong ghi nhớ, đo đạc hay tính toán. Số thực tìm được như thế được gọi là số làm tròn của số thực đã cho.
2. Làm tròn số với độ chính xác cho trước
Ví dụ: Làm tròn số \(123\) đến hàng chục. Tren trục số nằm ngang tìm khoảng cách giữa điểm biểu diễn số làm tròn và điểm biểu diễn số ban đầu.
Nhận xét: khi làm tròn số \(123\) đến hàng chục, ta được số \(120\). Trên trục số nằm ngang khoảng giữa điểm \(120\) và điểm \(123\) là: \(123-120=3.\) Khoảng cách đó không vượt quá \(5\). Ta nói số \(123\) được làm tròn đến số \(140\) với độ chính xác \(5\).

Ta nói số \(a\) được làm tròn đến số \(b\) với độ chính xác \(d\) nếu khoảng cách giữa điểm \(a\) và điểm \(b\) trên trục số không vượt quá \(d\).
Nhận xét
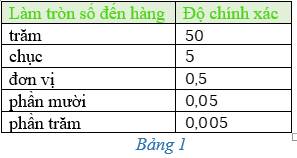
- Khi làm tròn số đến một hàng nào đó thì độ chính xác bằng nửa đơn vị của hàng làm tròn (Bảng 1)
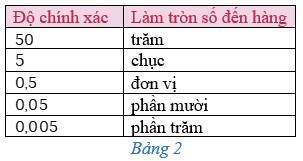
- Để làm tròn số với độ chính xác cho trước, ta có thể sử dụng cách nếu trong Bảng \(2\)
Chú ý: Trong đo đạc và tính toán thực tiễn, ta thường cố gắng làm tròn số thực với độ chính xác \(d\) càng nhỏ càng tốt. Trong thực tế, làm tròn số thực là một công việc có nhiều khó khăn. Tuy nhiên, người ta cũng biết một số cách để làm tròn số thực.
II. ƯỚC LƯỢNG
Trong thực tiễn, đôi lúc ta không quá quan tâm đến tính chính xác của kết quả tính toán mà chỉ cần ước lượng kết quả, tức là tìm một số gần sát kết quả tính toán.
Bạn có thể đăng câu hỏi về bài học này ở đây
