Bài học cùng chủ đề
- Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba
- Khảo sát và vẽ đồ thị hàm số hàm số phân thức hữu tỉ
- Nhận diện hàm số khi biết bảng biến thiên hoặc đồ thị hàm số
- Giao điểm của hai đồ thị hàm số
- Khảo sát sự biến thiên và vẽ đồ thị hàm số
- Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Khảo sát sự biến thiên và vẽ đồ thị hàm số SVIP
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
$a)$ $y=-x^3+3x+1;$
$b)$ $y=x^3 - 3x^2 + 4.$
Hướng dẫn giải:
$a)$ $y=-x^3+3x+1$.
1) Tập xác định của hàm số: $\mathbb R$.
2) Sự biến thiên:
+) Ta có: $y'=-3x^2+3$. Vậy $y'=0$ khi $x=-1$ hoặc $x=1$.
+) Trên khoảng $(-1;1)$, $y'>0$ nên hàm số đồng biến. Trên các khoảng $(-\infty;-1)$ và $(1;+\infty)$, $y'<0$ nên hàm số nghịch biến trên mỗi khoảng đó.
+) Hàm số đạt cực tiểu tại $x=-1$, giá trị cực tiểu $y_{CT}=-1$. Hàm số đạt cực đại tại $x=1$, giá trị cực đại $y_{CĐ} = 3$.
+) Giới hạn tại vô cực: $\displaystyle \lim_{x \rightarrow -\infty} y = +\infty$
$\displaystyle \lim_{x \rightarrow +\infty} y = -\infty$
+) Bảng biến thiên:
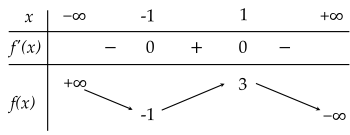
3) Đồ thị:
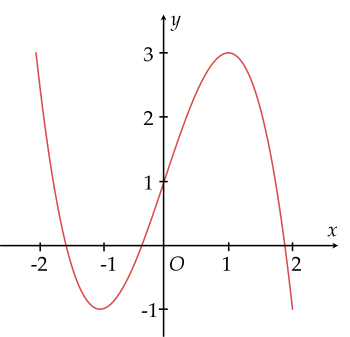
+) Giao điểm của đồ thị hàm số với trục tung là điểm $(0;1)$.
+) Ta thấy hàm số cắt trục tung tại $3$ điểm phân biệt.
+) Đồ thị hàm số có tâm đối xứng là điểm $(0;1)$.
$b)$ $y=x^3 - 3x^2 + 4.$
1) Tập xác định của hàm số: $\mathbb R$.
2) Sự biến thiên:
+) Giới hạn tại vô cực: $\displaystyle \lim_{x \rightarrow +\infty} y = +\infty$
$\displaystyle \lim_{x \rightarrow -\infty} y = -\infty$
$y' = 3x^2 - 6x;$
$y'=0 \Leftrightarrow 3x^2 - 6x = 0 \Leftrightarrow x=0$ hoặc $x=2$.
Bảng biến thiên của hàm số như sau:
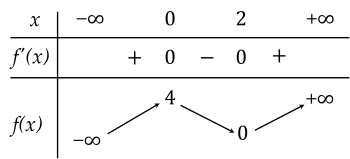
3) Đồ thị:
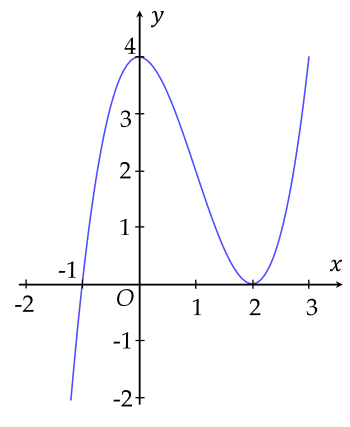
+) Giao điểm của đồ thị hàm số với trục tung là điểm $(0;4)$.
+) Giao điểm của đồ thị với trục hoành: $( -1 ; 0 )$ và $(2;0)$.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
$a) y= \dfrac{x+1}{x-2};$
$b) y= \dfrac{2x+1}{x-1}.$
Hướng dẫn giải:
$a) y= \dfrac{x+1}{x-2};$
1. Tập xác định của hàm số $\mathbb R$ \ $\{2\}$.
2. Sự biến thiên:
+) Ta có: $y' = -\dfrac{3}{(x-2)^2} < 0$ với mọi $x \neq 2$.
+) Hàm số nghịch biến trên từng khoảng \((- \infty; 2)\) và \((2; +\infty)\).
+) Hàm số không có cực trị.
+) Tiệm cận:
\[\displaystyle \lim_{x \to 2^-} y = \displaystyle \lim_{x \to 2^-} \dfrac{x+1}{x-2} = -\infty\]
\[\displaystyle \lim_{x \to 2^+} y =\displaystyle \lim_{x \to 2^+} \dfrac{x+1}{x-2} = +\infty\]
\[ \displaystyle \lim_{x \to +\infty} y = \displaystyle \lim_{x \to +\infty} \dfrac{x+1}{x-2} = 1; \]
\[\displaystyle \lim_{x \to -\infty} y = \displaystyle \lim_{x \to -\infty} \dfrac{x+1}{x-2} = 1.\]
+) Do đó, đồ thị của hàm số có tiệm cận đứng là đường thẳng \(x = 2\), tiệm cận ngang là đường thẳng \(y = 1\).
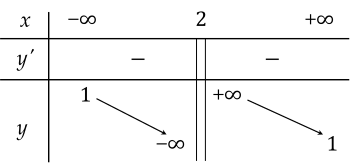
3. Đồ thị:

+) Giao điểm của đồ thị hàm số với trục tung là điểm \(\left(0; -{1}\right)\).
+) Giao điểm của đồ thị hàm số với trục hoành là điểm \((-1; 0)\).
+) Đồ thị hàm số nhận giao điểm \(I(2; 1)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng.
$b) y= \dfrac{2x+1}{x-1}.$
1. Tập xác định của hàm số $\mathbb R$ \ $\{1\}$.
2. Sự biến thiên:
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\[ \displaystyle \lim_{x \to -1^-} y = -\infty, \displaystyle \lim_{x \to -1^+} y = +\infty.\]
Vậy \[ x = 1 \] là tiệm cận đứng của đồ thị hàm số.
\[ \displaystyle \lim_{x \to +\infty} y = 2, \quad \displaystyle \lim_{x \to -\infty} y = 2.\]
Do đó, đường thẳng $y = 2$ là tiệm cận ngang của đồ thị hàm số.
\[y' = \dfrac{-3}{(x-1)^2} < 0 \] với mọi \[x \neq 1.\]
Bảng biến thiên:
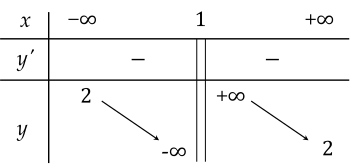
Hàm số nghịch biến trên mỗi khoảng \((- \infty; 1)\) và \((1; +\infty)\).
Hàm số không có cực trị.
3. Đồ thị:

Giao điểm của đồ thị với trục tung: \((0; -1)\).
Giao điểm của đồ thị với trục hoành: \(( -\dfrac{1}{2}; 0)\).
Đồ thị hàm số đi qua các điểm \((0; -1)\), \((-\dfrac{1}{2}; 0)\), \((-2; 1)\), \((2; 5)\), $\Big( \dfrac{5}{2};4 \Big)$ và $(4;3)$.
Khảo sát và vẽ đồ thị hàm số $y=\dfrac{x^2-x-1}{x-2}$.
Hướng dẫn giải:
1. Tập xác định của hàm số: $\mathbb{R} \setminus \{2\}$.
2. Sự biến thiên: Viết $y = x + 1 + \dfrac{1}{x-2}$.
Ta có: $y' = 1 - \dfrac{1}{(x-2)^2} = \dfrac{x^2 - 4x + 3}{(x-2)^2}$.
Vậy $y' = 0 \Leftrightarrow \dfrac{x^2 - 4x + 3}{(x-2)^2} = 0 \Leftrightarrow x = 1 \text{ hoặc } x = 3$.
Trên các khoảng $(-\infty; 1)$ và $(3; +\infty)$, $y' > 0$ nên hàm số đồng biến trên từng khoảng này.
Trên các khoảng $(1; 2)$ và $(2; 3)$, $y' < 0$ nên hàm số nghịch biến trên từng khoảng này.
Hàm số đạt cực đại tại $x = 1$ với $y_{\text{CĐ}} = 1$; hàm số đạt cực tiểu tại $x = 3$ với $y_{\text{CT}} = 5$.
$\lim\limits_{x \to -\infty} y = \lim\limits_{x \to +\infty} \dfrac{x^2 - x - 1}{x - 2} = \lim\limits_{x \to +\infty} \dfrac{x - 1 - \dfrac{1}{x}}{1 - \dfrac{2}{x}} = +\infty$.
Tiệm cận: $\lim\limits_{x \to 2} y = \lim\limits_{x \to 2} \left( x + 1 + \dfrac{1}{x-2} \right) = +\infty$.
$\lim\limits_{x \to 2} [y - (x + 1)] = \lim\limits_{x \to 2} \dfrac{1}{x-2} = +\infty$.
Do đó, đồ thị hàm số có tiệm cận đứng là đường thẳng $x = 2$, tiệm cận xiên là đường thẳng $y = x + 1$.
Bảng biến thiên:
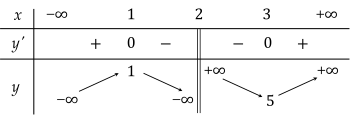
3. Đồ thị:

+) Giao điểm của đồ thị hàm số với trục tung là điểm $\Big( 0;\dfrac{1}{2} \Big).$
+) Ta có $y=0 \Leftrightarrow \dfrac{x^2-x-1}{x-2}$
$\Leftrightarrow x= \dfrac{1-\sqrt{5}}{2}$ hoặc $x=\dfrac{1+\sqrt{5}}{2}$.
Do đó giao điểm của đồ thị hàm số với trục hoành là các điểm $\Big(\dfrac{1-\sqrt{5}}{2} ; 0 \Big)$ và $\Big(\dfrac{1+\sqrt{5}}{2} ; 0 \Big)$.
Đồ thị hàm số nhận giao điểm $I(2;3)$ của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
