Đề số 1 (thời gian: 90') SVIP

Hướng dẫn giải:

a) $A=\sqrt{(2-\sqrt{3})^2}+2 \sqrt{3}$
$A=|2-\sqrt{3}|+2 \sqrt{3}$
$A=2-\sqrt{3}+2 \sqrt{3}$
$A=2+\sqrt{3}$
b) $B=\sqrt{18}-2 \sqrt{50}+3 \sqrt{8}+\sqrt[3]{27}$
$B=\sqrt{9.2}-2 \sqrt{25.2}+3 \sqrt{4.2}+\sqrt[3]{3.3 .3}$
$B=3 \sqrt{2}-2.5 \sqrt{2}+3.2 \sqrt{2}+3$
$B=3 \sqrt{2}-10 \sqrt{2}+6 \sqrt{2}+3$
$B=3-\sqrt{2}$
c) $C=\dfrac{4}{\sqrt{5}-1}-\dfrac{10}{\sqrt{5}}+\dfrac{\sqrt{125}}{\sqrt{5}}+\sqrt{2} \cdot \sqrt{\dfrac{5}{2}}$
$C=\dfrac{4 \cdot(\sqrt{5}+1)}{(\sqrt{5}-1)(\sqrt{5}+1)}-\dfrac{2 \cdot 5}{\sqrt{5}}+\sqrt{\dfrac{125}{5}}+\sqrt{2} \cdot \dfrac{\sqrt{5}}{\sqrt{2}}$
$C=\dfrac{4 \cdot(\sqrt{5}+1)}{(\sqrt{5})^2-1^2}-2 \sqrt{5}+\sqrt{25}+\sqrt{5}$
$C=\dfrac{4 \cdot(\sqrt{5}+1)}{5-1}-2 \sqrt{5}+5+\sqrt{5}$
$C=\dfrac{4 \cdot(\sqrt{5}+1)}{4}-\sqrt{5}+5$
$C=\sqrt{5}+1-\sqrt{5}+5$
$C=6$.

Hướng dẫn giải:

a) Ta có $x=25$ (thỏa mãn điều kiện), thay vào biểu thức $A$ ta có:
$$ A=\frac{\sqrt{25}-3}{\sqrt{25}+1}=\frac{5-3}{5+1}=\frac{2}{6}=\frac{1}{3} $$

Vậy khi $x=25$ thì $A=\dfrac{1}{3}$
b) Với $x>0, x \neq 4$, ta có:
$B=\left(\dfrac{x}{x-4}-\dfrac{1}{\sqrt{x}-2}\right): \dfrac{\sqrt{x}}{\sqrt{x}+2}$
$=\left[\dfrac{x}{(\sqrt{x}+2)(\sqrt{x}-2)}-\dfrac{1}{\sqrt{x}-2}\right]$
$=\dfrac{x-\sqrt{x}-2}{(\sqrt{x}+2)(\sqrt{x}-2)} \cdot \dfrac{\sqrt{x}+2}{\sqrt{x}}$
$=\dfrac{x-2 \sqrt{x}+\sqrt{x}-2}{\sqrt{x}(\sqrt{x}-2)}$
$=\dfrac{(\sqrt{x}-2)(\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}-2)}$
$=\dfrac{\sqrt{x}+1}{\sqrt{x}}$
Vậy $B=\dfrac{\sqrt{x}+1}{\sqrt{x}} x>0, x \neq 4$,
c) với $x>0, x \neq 4$, ta có
$P=A \cdot B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1} \cdot \dfrac{\sqrt{x}+1}{\sqrt{x}}=\dfrac{\sqrt{x}-3}{\sqrt{x}}=1-\dfrac{3}{\sqrt{x}}$
Với $x \in \mathbb{Z}, x>0, x \neq 4$,
+) Nếu $\sqrt{x}$ là số vô tỉ thì $\dfrac{3}{\sqrt{x}}$ là số vô tỉ nên $\mathrm{P}$ không là số nguyên (loại).
+) Nếu $\sqrt{x}$ là số nguyên nên $\mathrm{P}$ là số nguyên
$\Leftrightarrow \dfrac{3}{\sqrt{x}}$ là số nguyên
$\Leftrightarrow \sqrt{x}$ là ước dương của 3
$$ \begin{aligned} &\Leftrightarrow\left[\begin{array}{ll} \sqrt{x}=1 \\ \sqrt{x}=3 \end{array}\right. \\ &\Leftrightarrow\left[\begin{array}{ll} x=1 & \text { (nhận) } \\ x=9 & \text { (nhận) } \end{array}\right.\end{aligned}$$
Vậy $x \in\{1 ; 9\}$ thì $P$ có giá trị nguyên.

Hướng dẫn giải:

a) $\sqrt{4 x+20}-2 \sqrt{x+5}+\sqrt{9 x+45}=12$
Điều kiện: $x \geq-5$
Ta có:
$$\begin{aligned} &\sqrt{4 x+20}-2 \sqrt{x+5}+\sqrt{9 x+45}=12 \\ &\Leftrightarrow \sqrt{4(x+5)}-2 \sqrt{x+5}+\sqrt{9(x+5)}=12 \\ &\Leftrightarrow 2 \sqrt{x+5}-2 \sqrt{x+5}+3 \sqrt{x+5}=12 \\ &\Leftrightarrow 3 \sqrt{x+5}=12 \\ &\Leftrightarrow \sqrt{x+5}=4 \\ &\Leftrightarrow x+5=16 \\ &\Leftrightarrow x=11 \text { (thỏa mãn) } \end{aligned}$$
Vậy tập nghiệm của phương trình là $S=\{11\}$.
b) $\sqrt{x^2-10 x+25}=6$
Ta có:
$$ \begin{aligned} &\sqrt{x^2-10 x+25}=6 \\ &\Leftrightarrow \sqrt{(x-5)^2}=6 \\ &\Leftrightarrow|x-5|=6 \\ &\Leftrightarrow\left[\begin{array}{l} x-5=6 \\ x-5=-6 \end{array}\right. \\ &\Leftrightarrow\left[\begin{array}{l} x=11 \\ x=-1 \end{array}\right. \end{aligned}$$
Vậy tập nghiệm của phương trình là $S=\{11 ;-1\}$.

Hướng dẫn giải:

a)

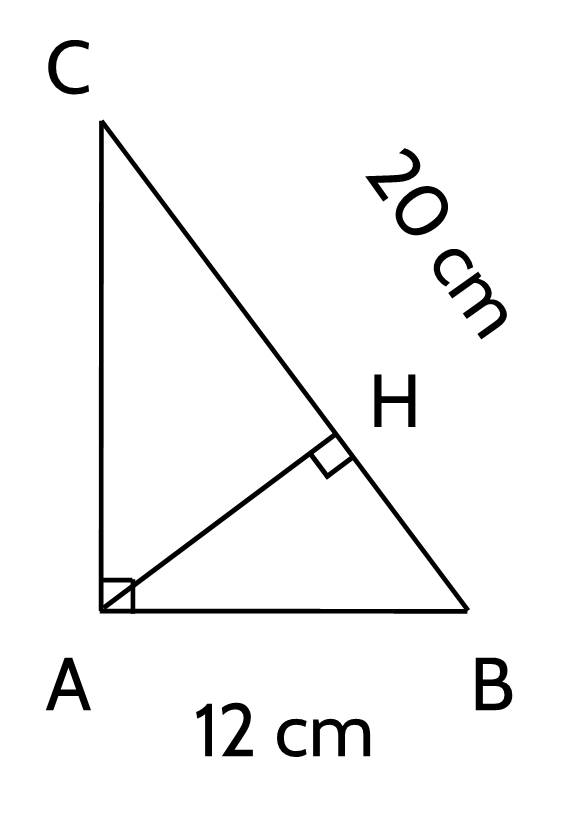
Xét tam giác $A B C$ vuông tại $A$, ta có:

$B C^2=A B^2+A C^2$ (Định lý Pytago)

Hay $20^2=12^2+A C^2 \Rightarrow A C^2=20^2-12^2=16^2 \Rightarrow A C=16 \mathrm{~cm}$

Xét tam giác $A B C$ vuông tại $A$ đường cao $A H$

Ta có: $A B \cdot A C=A H \cdot B C$ ( Hệ thức giữa đường cao và các cạnh góc vuông)

$$\Rightarrow A H=\dfrac{A B \cdot A C}{B C}=\dfrac{12 \cdot 16}{20}=9,6$$

Ta có: $\sin A B C=\dfrac{A C}{B C}=\dfrac{16}{20}=\dfrac{4}{5} \Rightarrow \widehat{A B C} \approx 53^{\circ}$

Vậy $A C=16 \mathrm{~cm}, A H=9,6$; tính được $\widehat{A B C} \approx 53^{\circ}$.

b)

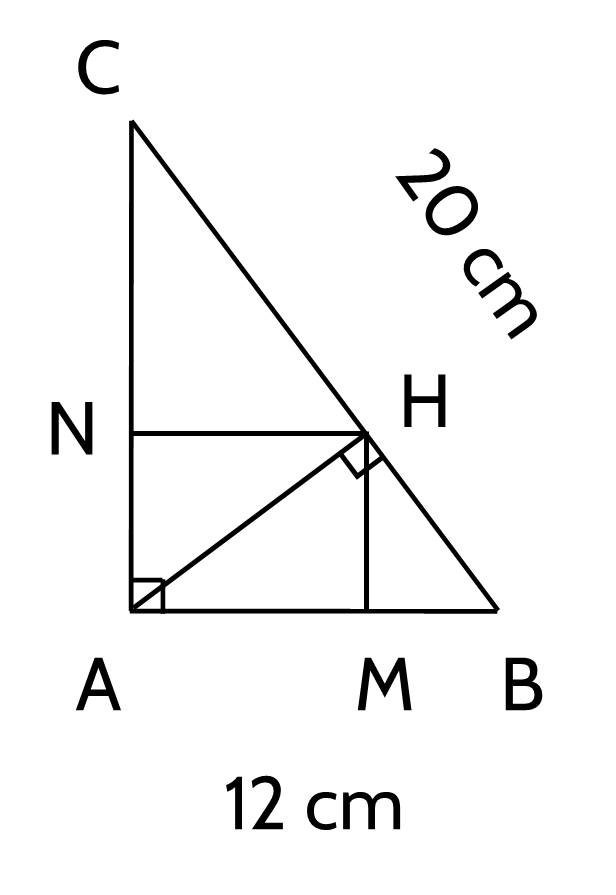
Xét $\triangle A H C$ đường cao $H N$

Có: $A N \cdot A C=A H^2$ ( Hệ thức giữa đường cao và các cạnh góc vuông) (1) $A C^2=A H^2+H C^2$ (Định lý Pytago) $\Rightarrow A H^2=A C^2-H C^2$

Từ (1), (2) $\Rightarrow A N . A C=A C^2-H C^2$

c) Ta có: $\widehat{M A N}=\widehat{A N H}=\widehat{A M H}=90^{\circ}$
$\Rightarrow A N H M$ là hình chữ nhật $\Rightarrow A H=M N$

Xét $\triangle A H B, \triangle A H C$ và $\triangle M H N$ có:

$\left\{\begin{array}{l}A M \cdot M B=M H^2 \\ A N \cdot N C=H N^2 \\ M N^2=H N^2+H M^2\end{array}\right.$ $\Rightarrow A M \cdot M B+A N \cdot N C=H N^2+H M^2=M N^2=A H^2$

d) Xét tam giác $A B C$ vuông tại $A$, đường cao $A H$, ta có:
$\left\{\begin{array}{l}A C^2=C H \cdot B C \\ A B^2=B H \cdot B C\end{array} \Rightarrow \dfrac{A B^2}{A C^2}=\dfrac{B H \cdot B C}{C H \cdot B C}=\dfrac{B H}{C H}\right.$

Lại có: $H M / / A C \Rightarrow \dfrac{B M}{A M}=\dfrac{B H}{C H}($ định lý Ta-let $)(4)$

$H N / / A B \Rightarrow \dfrac{H N}{A B}=\dfrac{N C}{A C} \Rightarrow \dfrac{A B}{A C}=\dfrac{N H}{C N}$

Từ (3), (4),(5) $\Rightarrow \dfrac{A B^2 \cdot A B}{A C^2 \cdot A C}=\dfrac{B M}{A M} \cdot \dfrac{N H}{C N}$ hay $\tan ^3 C=\dfrac{A B^3}{A C^3}=\dfrac{B M}{C N}$.

Hướng dẫn giải:

Từ giả thiết $(\sqrt{a}+1)(\sqrt{b}+1) \geq 4 \Leftrightarrow \sqrt{a b}+\sqrt{a}+\sqrt{b}+1 \geq 4 \Leftrightarrow \sqrt{a b}+\sqrt{a}+\sqrt{b} \geq 3$

Áp dụng bất đẳng thức Cô-si cho 2 số thực dương $a, b: a+b \geq 2 \sqrt{a b} \Leftrightarrow \dfrac{a+b}{2} \geq \sqrt{a b}$(1)

Ta có $(\sqrt{a}-1)^2 \geq 0 \Leftrightarrow a-2 \sqrt{a}+1 \geq 0 \Leftrightarrow \dfrac{a+1}{2} \geq \sqrt{a}$ Và $(\sqrt{b}-1)^2 \geq 0 \Leftrightarrow b-2 \sqrt{b}+1 \geq 0 \Leftrightarrow \dfrac{b+1}{2} \geq \sqrt{b}$

Từ $(1), (2), (3)$ ta suy ra
$\dfrac{a+b}{2}+\dfrac{a+1} {2}+\dfrac{b+1}{2} \geq \sqrt{a b}+\sqrt{a}+\sqrt{b}$
$$ \begin{aligned} &\Leftrightarrow \dfrac{2 a+2 b+2}{2} \geq \sqrt{a b}+\sqrt{a}+\sqrt{b} \\ &\Leftrightarrow a+b+1 \geq \sqrt{a b}+\sqrt{a}+\sqrt{b} \\ &\text { Mà } \sqrt{a b}+\sqrt{a}+\sqrt{b} \geq 3 \text { nên } a+b+1 \geq 3 \Leftrightarrow a+b \geq 2 . \end{aligned} $$

$$ P=\dfrac{a^2}{b}+\dfrac{b^2}{a}=\left(\dfrac{a^2} {b}+b\right)+\left(\dfrac{b^2}{a}+a\right)-(a+b)$$
Với $a, b$ là các số thực dương ta áp dụng bất đẳng thức Cô-si:
$$\begin{aligned} &\Leftrightarrow P \geq 2 \sqrt{\dfrac{a^2}{b}} \cdot b+2 \sqrt{\dfrac{b^2}{a}} \cdot a-(a+b) \\ &\Leftrightarrow P \geq 2 a+2 b-(a+b) \\ &\Leftrightarrow P \geq a+b \\ &\Leftrightarrow P \geq 2 \end{aligned}$$
Dấu "=" xảy ra khi và chỉ khi $a=b=1$.
Vậy giá trị nhỏ nhất của $P=2$ khi $a=b=1$.