Hình thang cân SVIP

I. NHẬN BIẾT HÌNH THANG CÂN

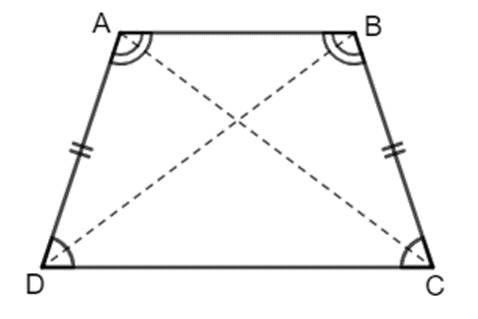
Hình thang cân ABCD có: 

• Hai cạnh đáy AB và CD song song với nhau;
• Hai cạnh bên bằng nhau: \(AD=BC\); hai đường chéo bằng nhau: \(AC=BD\);
• Hai góc kề với cạnh đáy CD bằng nhau, tức là hai góc CDA và BCD bằng nhau; hai góc kề với cạnh đáy AB bằng nhau, tức là hai góc DAB và ABC bằng nhau.

II. CHU VI VÀ DIỆN TÍCH CỦA HÌNH THANG CÂN

• Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang đó;
• Diện tích của hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.

Ví dụ:

a) Trong hình vẽ dưới đây, hình nào là hình thang cân?

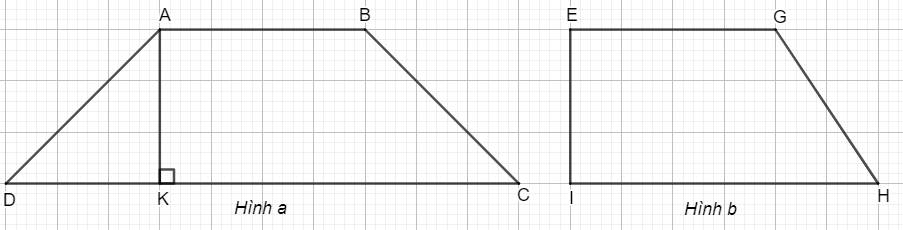
b) Biết mỗi hình vuông có cạnh là 2 cm. Tính diện tích của hai hình thang ABCD và EGHI.

Giải

a) Hình a là hình thang cân. Hình b không phải là hình thang cân.

b) Ta có: \(AB=8\) cm; \(CD=20\) cm; \(AK=6\) cm. Do đó, diện tíc hình thang ABCD là:

\(S_1=\dfrac{\left(8+20\right).6}{2}=84\) (cm²).

Do \(EG=8\) cm, \(HI=12\) cm, \(EI=6\) cm nên diện tích của hình thang EGHI là:

\(S_2=\dfrac{\left(8+12\right).6}{2}=60\) (cm²).