Bài học cùng chủ đề
- Hệ bất phương trình bậc nhất hai ẩn
- Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn
- Ứng dụng hệ bất phương trình bậc nhất hai ẩn để tìm GTLN - GTNN
- Ứng dụng hệ bất phương trình bậc nhất hai ẩn để giải các bài toán thực tế
- Điểm có thuộc miền nghiệm của hệ bất phương trình hay không?
- Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn
- Ứng dụng của hệ bất phương trình bậc nhất hai ẩn
- Phiếu bài tập: Hệ bất phương trình bậc nhất hai ẩn
- Hệ bất phương trình bậc nhất hai ẩn
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Hệ bất phương trình bậc nhất hai ẩn SVIP
I. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Hệ bất phương trình bậc nhất hai ẩn \(x,y\) là một hệ gồm một số bất phương trình bậc nhất hai ẩn \(x,y\). Mỗi nghiệm chung của các bất phương trình trong hệ được gọi là một nghiệm của hệ bất phương trình đó.
Ví dụ. Hệ bất phương trình \(\left\{{}\begin{matrix}x+y\le10\\2x-y>3\end{matrix}\right.\) là một hệ bất phương trình bậc nhất hai ẩn \(x\) và \(y\) và cặp số \(\left(x;y\right)=\left(3;1\right)\) là một nghiệm của hệ bất phương trình bậc nhất hai ẩn đã cho.
II. BIỂU DIỄN MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Miền nghiệm của hệ bất phương trình là giao các miền nghiệm của các bất phương trình trong hệ.
Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn, ta làm như sau:
- Trong cùng mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
- Phần không bị gạch là miền nghiệm cần tìm.
Ví dụ. Xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(\left\{{}\begin{matrix}x-2y< 0\\x+3y>-2\end{matrix}\right.\) trên mặt phẳng tọa độ.
Giải
Xác định miền nghiệm \(D_1\) của bất phương trình \(x-2y< 0\) và gạch bỏ miền còn lại.
- Vẽ đường thẳng \(d_1:x-2y=0\).
- Xét điểm \(M\left(0;1\right)\) có \(1.0-2.1=-2< 0\) nên tọa độ điểm \(M\left(0;1\right)\) nằm trong miền nghiệm \(D_1\).
Do đó miền nghiệm \(D_1\) của bất phương trình \(x-2y< 0\) là nửa mặt phẳng bờ \(d_1\) chứa điểm \(M\left(0;1\right)\).
Tương tự miền nghiệm \(D_2\) của bất phương trình \(x+3y>-2\) là nửa mặt phẳng bờ \(d_2\) chứa điểm \(M\left(0;1\right)\).
Khi đó miền không bị gạch chính là giao các miền nghiệm của các bất phương trình trong hệ. Vậy miền nghiệm của hệ bất phương trình đã cho là miền không bị gạch trong hình vẽ sau:
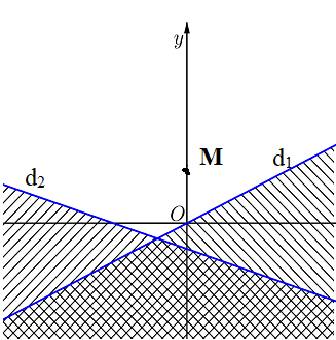
III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN
Bài toán: Một nhà máy sản xuất sử dụng ba loại máy để sản xuất sản phẩm \(A\) và sản phẩm \(B\) trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm \(A\) lãi \(4\) triệu đồng người ta sử dụng máy \(I\) trong \(1\) giờ, máy \(II\) trong \(2\) giờ và máy \(III\) trong \(3\) giờ. Để sản xuất ra một tấn sản phẩm \(B\) lãi được \(3\) triệu đồng, người ta sử dụng máy \(I\) trong \(6\) giờ, máy \(II\) trong \(3\) giờ và máy \(III\) trong \(2\) giờ. Biết máy \(I\) chỉ hoạt động không quá \(36\) giờ, máy \(II\) hoạt động không quá \(23\) giờ và máy \(III\) hoạt động không quá \(27\) giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất?
Giải
Gọi \(x,y\) lần lượt là số tấn cần sản xuất của sản phẩm loại \(A\) và sản phẩm loại \(B\) \(\left(x\ge0;y\ge0\right)\).
Thời gian hoạt động của máy \(I:x+6y\);
Thời gian hoạt động của máy \(II:2x+3y\);
Thời gian hoạt động của máy \(III:3x+2y\).
Số tiền lãi thu được: \(F=4x+3y\) (triệu đồng).
Bài toán trở thành tìm \(x,y\) là nghiệm của hệ bất phương trình \(\left\{{}\begin{matrix}x\ge0;y\ge0\\x+6y\le36\\2x+3y\le23\\3x+2y\le27\end{matrix}\right.\)(*)
để \(F=4x+3y\) đạt giá trị lớn nhất.
Ta xác định miền nghiệm của hệ bất phương trình (*).
Miền nghiệm của hệ bất phương trình (*) là miền ngũ giác \(ABCDO\) (hình vẽ) có \(A\left(0;6\right)\);\(B\left(\dfrac{10}{3};\dfrac{49}{9}\right);C\left(7;3\right);D\left(9;0\right)O\left(0;0\right)\).
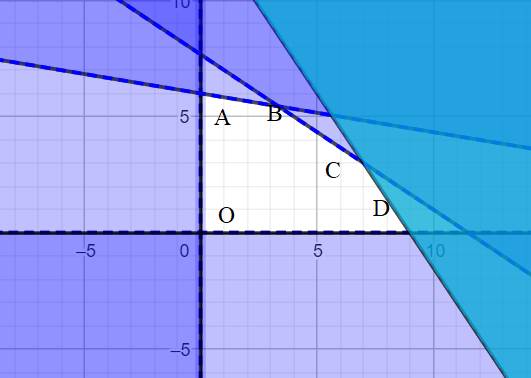
Biểu thức \(F=4x+3y\) đạt được giá trị lớn nhất tại một trong các đỉnh của ngũ giác \(ABCDO\) .
Tính giá trị biểu thức \(F=4x+3y\) tại cặp số \(\left(x;y\right)\) là tọa độ các đỉnh của ngũ giác \(ABCDO\) và so sánh các giá trị đó ta được \(F\) đạt giá trị lớn nhất bằng 37 khi \(x=7;y=3\) ứng với tọa độ đỉnh \(C\).
Vậy để tiền lãi được nhiều nhất, nhà máy nên sản xuất \(7\) tấn sản phẩm loại \(A\) và \(3\) tấn sản phẩm loại \(B\).
Bạn có thể đăng câu hỏi về bài học này ở đây
