Hàm số mũ - Hàm số lôgarit SVIP

1, Hàm số mũ $y=a^x$

⚡️Tập xác định: $D = \mathbb{R}$.

⚡️Tập giá trị: $T=(0; + \infty)$.

⚡️Sự biến thiên:

Nếu $a>1$ thì hàm số $y=a^x$ đồng biến thì $a^{f(x)} > a^{g(x)} \Leftrightarrow f(x) > g(x)$.

Nếu $0<a<1$ thì hàm số $y=a^x$ nghịch biến thì $a^{f(x)} >a^{g(x)} \Leftrightarrow f(x) < g(x)$.

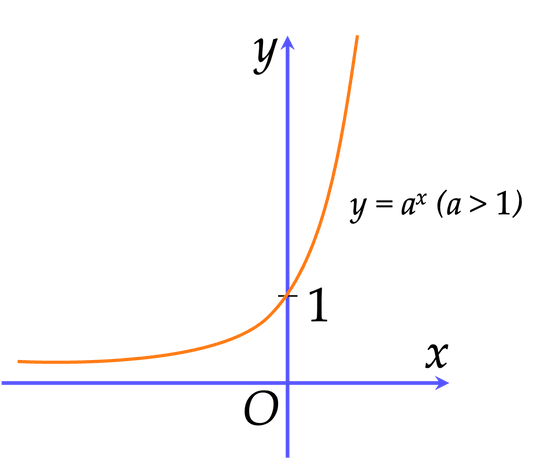
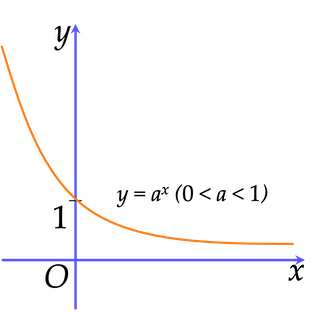
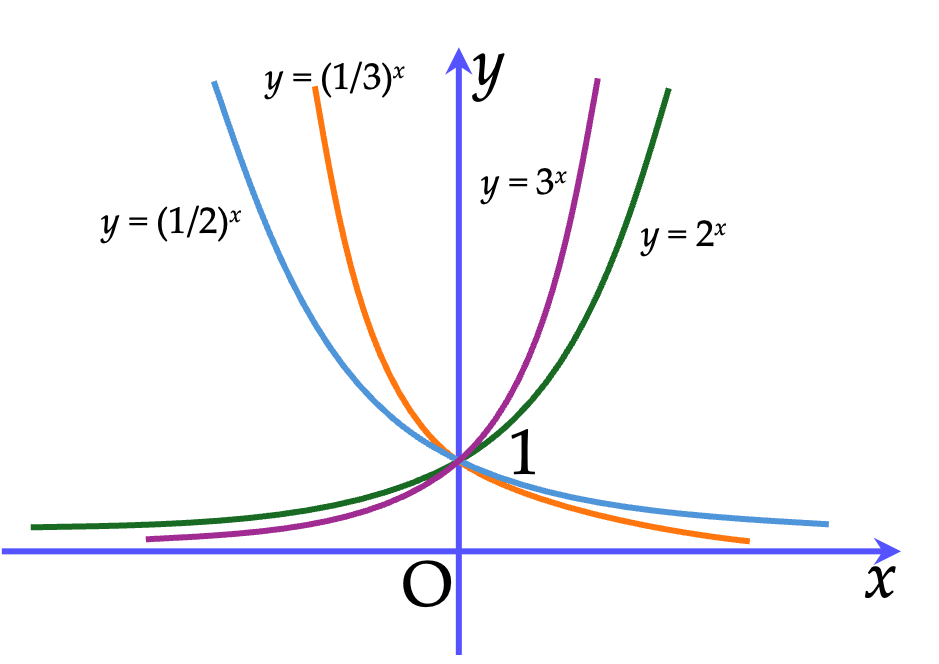
⚡️Đồ thị hàm số

Nhận xét:

Đồ thị đi qua điểm $(0;1)$.

Đồ thị luôn nằm ở phía trên trục hoành.

2, Hàm số lôgarit $y= \log_a x$

⚡️Tập xác định: $D =(0; + \infty)$.

⚡️Tập giá trị: $T=\mathbb{R}$.

⚡️Sự biến thiên:

Nếu $a>1$ thì hàm số $y= \log_a x$ đồng biến trên $D$ thì $ \log_a {f(x)} > \log_a {g(x)} \Leftrightarrow f(x) > g(x)$.

Nếu $0<a<1$ thì hàm số $y= \log_a x$ nghịch biến trên $D$ thì $ \log_a {f(x)} > \log_a {g(x)} \Leftrightarrow f(x) > g(x)$.

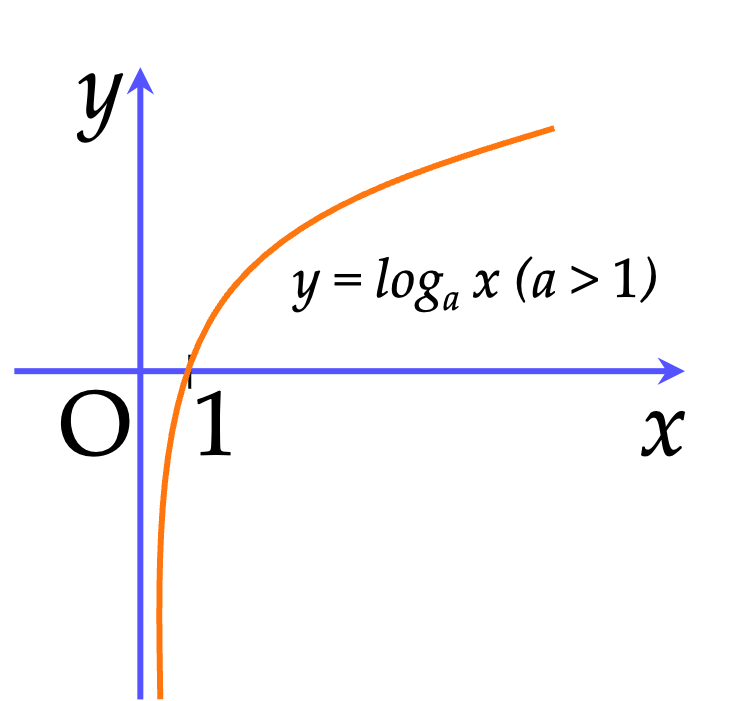
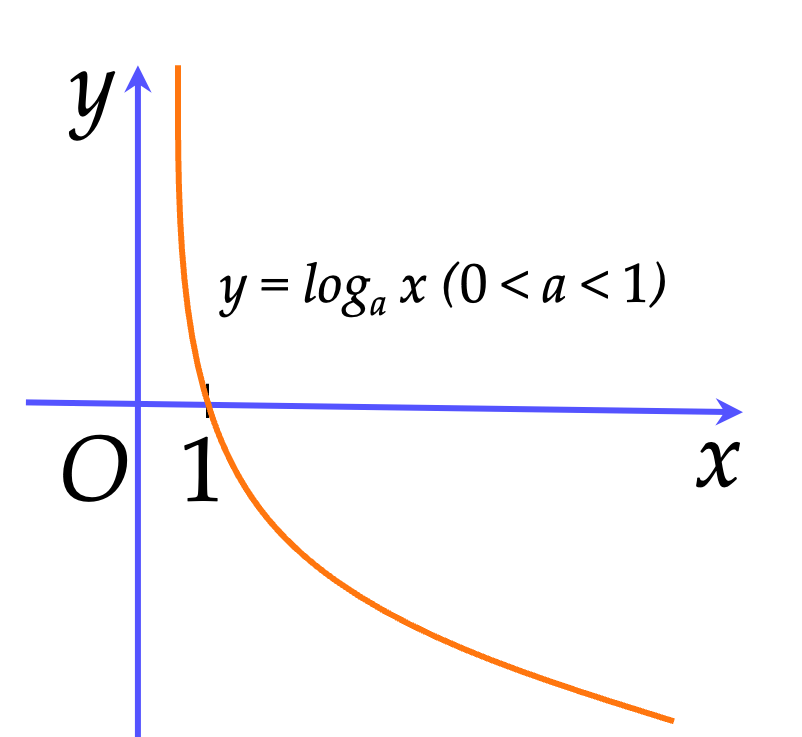
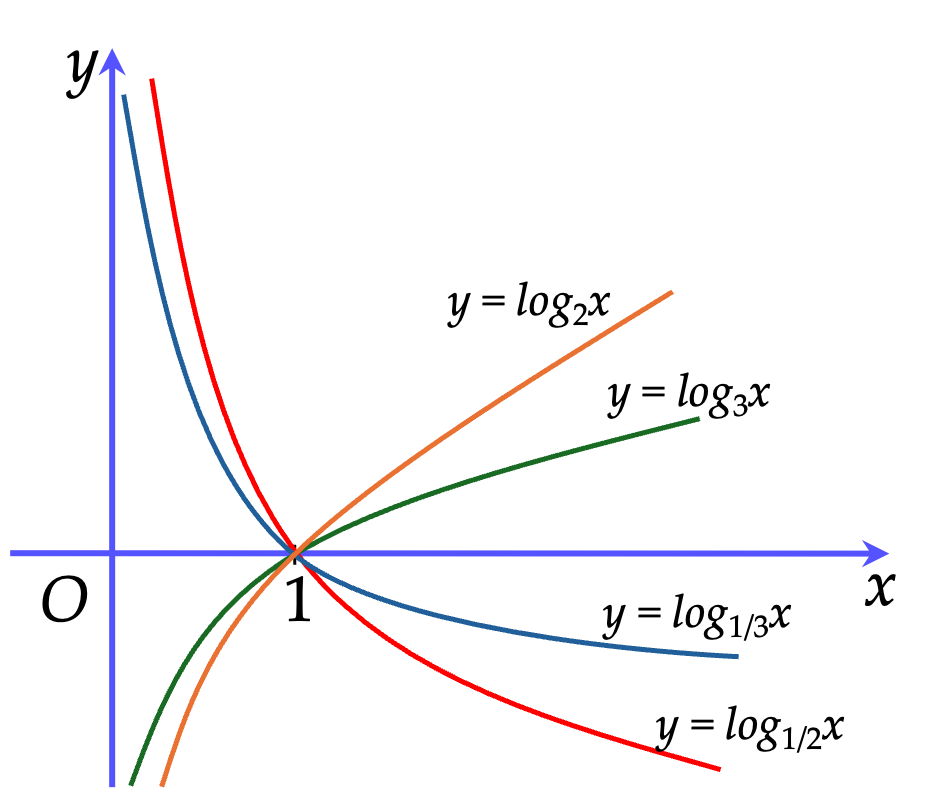
⚡️Đồ thị hàm số:

Nhận xét:

Đồ thị đi qua điểm $(1;0)$.

Đồ thị liên tục trên $(0; +\infty)$.

Đồ thị luôn nằm ở bên phải trục tung.

Chú ý: Đồ thị hàm số $y=a^x$ đối xứng $y = \log_a x$ qua $y=x$ (đường phân giác góc phần tư thứ nhất).

 Dạng 1. Tập xác định của hàm số

Phương pháp

Xét $a \ge 1$: 

⚡️Hàm số $y=a^{f(x)}$ xác định $ \Leftrightarrow f(x)$ xác định.

⚡️Hàm số $y= \log_a {f(x)}$ xác định $ \Leftrightarrow f(x) > 0$.

Chú ý: 

⚡️Dấu của tam thức bậc hai $f(x)=ax^2+bx+c (a \ne 0)$:

Nếu $\Delta < 0$ thì $f(x)$ cùng dấu với hệ số $a$ với mọi $x \in \mathbb{R}$.

Nếu $\Delta=0$ thì $f(x)$ cùng dấu với hệ số $a$ với mọi $x \ne \dfrac{-b}{2a}$ và $f \Big( \dfrac{-b}{2a} \Big) = 0$.

Nếu $\Delta>0$ thì $f(x)$ có hai nghiệm phân biệt $x_1$ và $x_2$ $(x_1 < x_2)$. Khi đó $f(x)$ cùng dấu với hệ số $a$ với mọi $x \in (-\infty; x_1) \cup (x_2; +\infty)$; $f(x)$ trái dấu với hệ số $a$ với mọi $x \in (x_1; x_2)$.

Ví dụ 1. Tìm tập xác định của hàm số $y= \log_2 {(2x-3)}$.

Lời giải

Điều kiện: $2x-3 >0 \Leftrightarrow x > \dfrac{3}{2}$. 

Vậy tập xác định là $D=\Big( \dfrac{3}{2}; +\infty \Big)$.

Ví dụ 2. Tìm tập xác định của hàm số $y= \log_2 {(x^2-9)}$.

Lời giải

Điều kiện: $x^2-9 >0 \Leftrightarrow$ $\left[ \begin{aligned} & x>3 \\ & x<-3 \\ \end{aligned}\right.$ 

Vậy tập xác định là $D=(-\infty;-3) \cup (3; +\infty)$.

Ví dụ 3. Tìm tập xác định của hàm số $y=7^{ \sqrt{x-3}}$.

Lời giải

Điều kiện: $x-3 \ge 0 \Leftrightarrow x \ge 3$. 

Vậy tập xác định là $D=[3; +\infty)$.

Dạng 2. Sự biến thiên của hàm số

Phương pháp

Xét $0 < a \ne 1$	Hàm số mũ $y=a^x$	Hàm số $y = \log_ax$
Sự biến thiên	⚡️ $a>1 \to$ hàm số đồng biến. ⚡️ $0<a<1 \to$ hàm số nghịch biến.	⚡️ $a>1 \to$ hàm số đồng biến. ⚡️ $0<a<1 \to$ hàm số nghịch biến.

Ví dụ 4. Xét sự biến thiên của các hàm số sau:

a) $y= \log_{4- \sqrt{3}} x$.

b) $y= \log_{1- \sqrt{\frac{2 \, 018}{2 \, 019}}} x$.

Lời giải

a) TXĐ: $D=(0; +\infty)$

$4- \sqrt{3} > 1 \to$ hàm số $y= \log_{4- \sqrt{3}} x$ đồng biến trên $(0; +\infty)$.

b) TXĐ: $D=(0; +\infty)$

$0< 1- \sqrt{\dfrac{2 \, 018}{2 \, 019}} < 1 \to$ hàm số $y= \log_{1- \sqrt{\frac{2 \, 018}{2 \, 019}}} x$ nghịch biến trên $(0; +\infty)$.

Ví dụ 5. Xét sự biến thiên của các hàm số sau:

a) $y= \Big( \dfrac{1}{2} \Big)^x$.

b) $y=( \pi - \sqrt{2})^x$.

Lời giải

a) TXĐ: $D= \mathbb{R}$

$0 < \dfrac{1}{2} < 1 \to$ hàm số $y= \Big( \dfrac{1}{2} \Big)^x$ nghịch biến trên $\mathbb{R}$.

b) TXĐ: $D= \mathbb{R}$

$\pi - \sqrt{2} > 1 \to$ hàm số $y=( \pi - \sqrt{2})^x$ đồng biến trên $\mathbb{R}$.

Dạng 3. Đồ thị hàm số

Phương pháp

Xét $0 < a \ne 1$		Hàm số mũ $y=a^x$	Hàm số $y = \log_ax$
Đồ thị
Nhận xét		Nằm bên trên $Ox$. Luôn đi qua điểm $(0;1)$.	Nằm bên phải $Oy$. Luôn đi qua điểm $(1;0)$.
		Đồ thị hàm số $y=a^x$ đối xứng $y = \log_a x$ qua $y=x$ (đường phân giác góc phần tư thứ nhất).

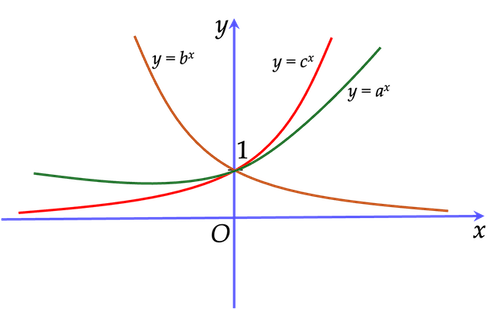
Ví dụ 6. Cho các hàm số $y=a^x, y=b^x, y=c^x$ lần lượt có đồ thị như hình vẽ bên dưới. Hãy so sánh $a,b,c$. 

Lời giải

Ta thấy $y=b^x$ là hàm số mũ nghịch biến nên $0<b<1 (1)$.

Tương tự, ta có:  $y=a^x,y=c^x$ là hàm số mũ đồng biến nên $a,c>1$.

Kẻ đường thẳng $x=1$ cắt đồ thị hàm số $y=a^x,y=c^x$ tại hai điểm $(1;a)$ và $(1;c)$.

Từ đồ thị, ta thấy $c>a>1 (2) $

Từ $(1)$ và $(2)$ suy ra $c>a>b$.

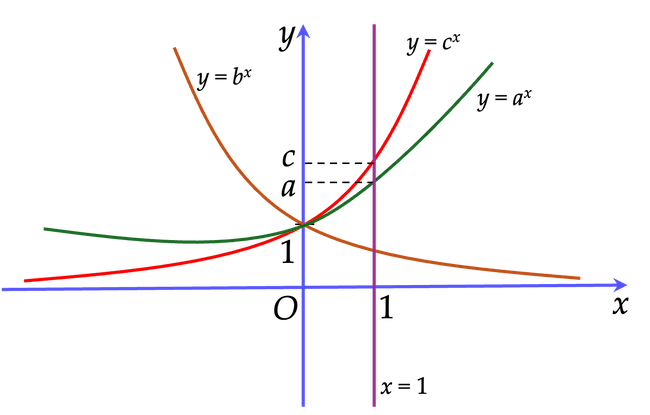
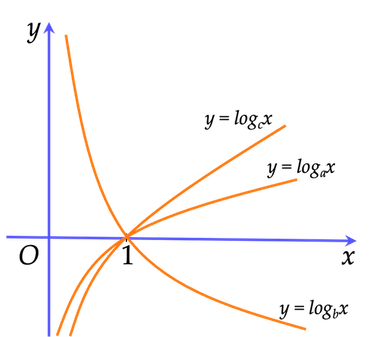
Ví dụ 7. Cho ba số thực dương $a, \, b, \, c$ khác $1$. Đồ thị các hàm số $y= \log_a x, \, y= \log_b x, \, y= \log_c x$ được cho trong hình vẽ dưới đây. So sánh các số $a, \, b, \, c$.

 Lời giải

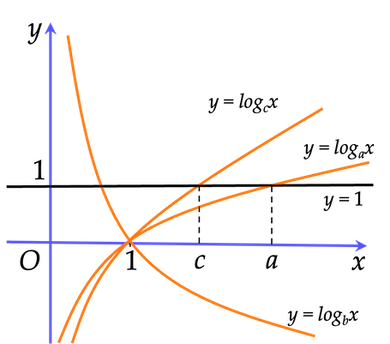
Dựa vào đồ thị, ta thấy hàm số $y= \log_b x$ nghịch biến trên $(0; +\infty) \Rightarrow 0<b<1. (1)$

Mặt khác, hàm số $y= \log_a x, \, y= \log_c x$ đồng biến trên $(0; +\infty) \Rightarrow a,c>1$.

Kẻ đường thẳng $y=1$ cắt đồ thị hàm số $y=a^x,y=c^x$ tại hai điểm $(a;1)$ và $(c;1)$.

Từ đồ thị, ta thấy $a>c>1. (2) $

Từ $(1)$ và $(2)$ suy ra $a>c>b$.