Đường vuông góc và đường xiên SVIP

1. QUAN HỆ GIỮA CẠNH VÀ GÓC TRONG MỘT TAM GIÁC

Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn và ngược lại, đối diện với cạnh lớn hơn là góc lớn hơn.

Ví dụ 1. 

a) Trong tam giác $ABC$ có $\widehat {A}>\widehat {B}$ nên $BC>AC$.

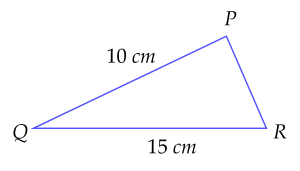
 a) Trong tam giác $PQR$ có $QR>PQ$ nên $\widehat {P}>\widehat {R}$.

Ví dụ 2. 

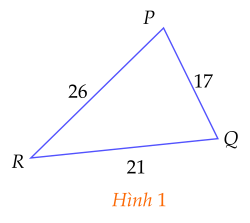
a) Sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác $PQR$ trong Hình $1$

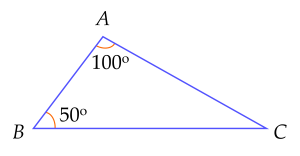
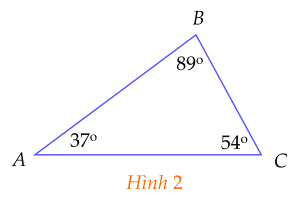
b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác $ABC$ trong Hình $2$.

 Lời giải 

a) Do $PQ < RQ < RP$ nên $\widehat {R}<\widehat {P}<\widehat {Q}$.

Do đó số đo các góc theo thứ tự từ nhỏ đến lớn là: $\widehat {R}$, $\widehat {P}$, $\widehat {Q}$.

b) Do $\widehat {A}<\widehat {C}<\widehat {B}$ nên $BC < AB < AC$.

Do đó độ dài các cạnh theo thứ tự từ nhỏ đến lớn là: $BC$; $AB$; $AC$.

2. MỐI QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN 

 ĐỊNH NGHĨA

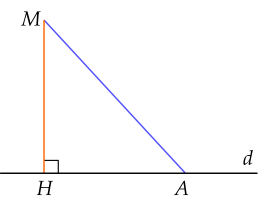
Từ một điểm $M$ không nằm trên đường thẳng$d$ $d$, kẻ một đường thẳng vuông góc với $d$ tại$H$ $H$. Trên $d$ lấy điểm $A$ không trùng với điểm $H$. Khi đó:

⚡ Đoạn thẳng $MH$ gọi là đoạn vuông góc hay đường vuông góc kẻ từ điểm $M$ đến đường thẳng $d$.

⚡ Đoạn thẳng $MA$ gọi là một đường xiên kẻ từ điểm $M$ đến đường thẳng $d$.

⚡ Độ dài đoạn $MH$ được gọi là khoảng cách từ điểm$$ $M$ đến đường thẳng$$ $d$.

Ví dụ 3. 

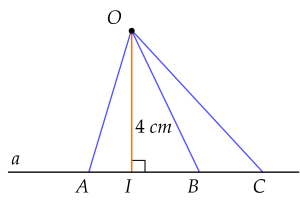
a) Hình chiếu của điểm $O$ trên đường thẳng$a$ $a$ và khoảng cách từ điểm $O$ đến đường thẳng $$a$a$.

b) Các đường xiên kẻ từ điểm $O$ đến đường thẳng $a$.

 Lời giải

a) Hình chiếu của điểm $O$ trên đường thẳng $a$ là điểm $I$. Khoảng cách từ điểm $O$ đến đường thẳng$a$ $a$ là $OI=4$ cm.

b) Các đoạn thẳng $OA,\,OB,\,OC$ là các đường xiên kẻ từ điểm $O$ đến đường thẳng$a$ $a$.

 ĐỊNH LÍ

Trong số các đoạn thẳng nối từ một điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên.

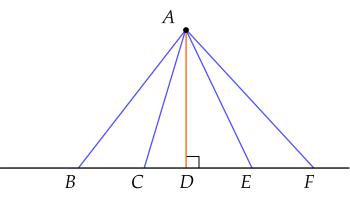
Ví dụ 4. Trong hình dưới đây, tìm đường vuông góc và đường xiên kẻ từ điểm $A$$A$ đến đường thẳng $BF$. Trong số các đường này, đường nào ngắn nhất?

 Lời giải  

Đường vuông góc kẻ từ $A$ đến đường thẳng $BF$: $AD$.

Đường xiên kẻ từ $A$ đến đường thẳng $BF$: $AB$, $AC$, $AE$, $AF$.

Khi đó $AD$ là đường ngắn nhất trong các đường $AB$, $AC$, $AD$, $AE$, $AF$.