Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đường trung trực của đoạn thẳng SVIP
I. ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy.
Ví dụ 1. Trong hình dưới đây đường thẳng $xy$ là đường trung trực của đoạn thẳng $AB$ vì $xy$ vuông góc với $AB$ tại trung điểm $O$ của đoạn thẳng $AB$.
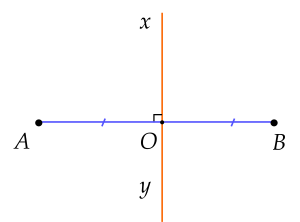
Câu hỏi:
@204414749412@
II. TÍNH CHẤT CỦA ĐƯỜNG TRUNG TRỰC
Điểm nằm trên trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
Ví dụ 2. Cho đoạn thẳng $AB$ có $d$ là đường trung trực. Lấy $M, N \in d$ sao cho $MA = 3$, $NA=5$. Khi đó độ dài các đoạn thẳng $MB,\,NB$ bằng bao nhiêu?
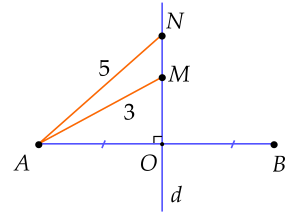
Lời giải
Vì $M,\,N$ thuộc đường trung trực của đoạn thẳng $AB$ nên theo định lí 1, ta có:
$MB=MA=3$; $NB=NA=5$.
Câu hỏi:
@204414952925@
Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Ví dụ 3. Cho đoạn thẳng $AB$, $O$ là trung điểm của $AB$. Hai điểm $P,\,Q$ khác $O$ thỏa mãn $PA=PB$, $QA=QB$. Chứng minh rằng ba điểm $P$, $O$, $Q$ thẳng hàng.
Lời giải
Hai điểm $P$, $Q$ cách đều hai đầu mút của đoạn thẳng $A$, $B$ nên cùng nằm trên đường trung trực của đoạn thẳng $AB$. Mặt khác $O$ là trung điểm của đoạn $AB$ nên $P,\,Q,\,O$ thẳng hàng.
Ví dụ 4. Cho hai điểm $M$ và $N$ nằm trên đường trung trực $d$ của đoạn thẳng $EF$. Chứng minh rằng $\Delta EMN=\Delta FMN$.
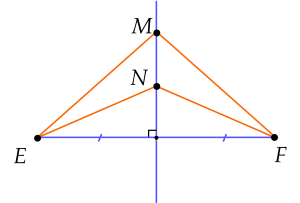
Lời giải
Do $M$ và $N$ nằm trên đường trung trực của đoạn thẳng $EF$ nên $ME = MF$ và $NE = NF$.
Xét $\Delta EMN$ và $\Delta FMN$
có:
$ME = MF$
$NE = NF$
$MN$: cạnh chung.
Do đó $\Delta EMN=\Delta FMN$ (c - c - c).
Câu hỏi:
@204415183741@
DỰNG ĐƯỜNG TRUNG TRỰC BẰNG THƯỚC THẲNG VÀ COMPA
Bước 1: Lấy $A$ làm tâm vẽ cung tròn bán kính lớn hơn $\dfrac12 AB$.

Bước 2: Lấy $B$ làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên.

Bước 3: Hai cung tròn này cắt nhau tại $M$ và $N$. Dùng thước vẽ đường thẳng $MN$. Khi đó đường thẳng $MN$ là đường trung trực của đoạn $AB$.
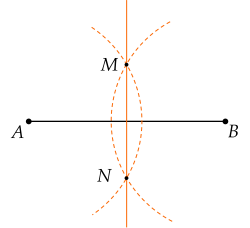
Bạn có thể đăng câu hỏi về bài học này ở đây
