Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Câu 1. (2,0 điểm). Theo công bố chính thức từ hãng sản xuất, xe ô tô của ông An có mức tiêu thụ nhiên liệu cho mỗi $100$ km trên các loại đường như sau:
| Đường hỗn hợp | Đường đô thị | Đường cao tốc |
| $9,9$ lít | $13,9$ lít | $7,5$ lít |
a) Để đi được $30$ km đường đô thị, xe của ông An cần tối thiểu bao nhiêu lít xăng?
b) Với $4,17$ lít xăng, xe của ông An chạy được tối đa bao nhiêu ki-lô-mét đường cao tốc?
c) Ông An lái xe đi từ nhà về quê. Từ nhà ra đến đường cao tốc, ông An phải lái xe $20$ km đường đô thị. Sau đó khi chạy tiếp $80$ km đường cao tốc, ông An còn phải chạy tiếp $30$ km đường hỗn hợp. Em hãy tính xem xe của ông An tiêu thụ hết bao nhiêu lít xăng?
Hướng dẫn giải:
a) Khi xe di chuyển trên cùng một loại đường thì chiều dài quãng đường tỉ lệ thuận với lượng xăng tiêu thụ. Ta có bảng tóm tắt sau:
| Loại đường | Chiều dài quãng (km) | Lượng xăng tiêu thụ (lít) |
| Đô thị | $100$ | $13,9$ |
| $30$ | $x$ |
Từ đó $x=(30 .13,9) \, : \, 100=4,17$.
Do đó, để đi được $30$ km đường đô thị cần tối thiểu $4,17$ lít xăng.
b)
Tương tự, ta có
| Loại đường | Chiều dài quãng (km) | Lượng xăng tiêu thụ (lít) |
| Cao tốc | $100$ | $7,5$ |
| $y$ | $4,17$ |
Do đó $y = (100.4,17) \, : \, 7,5 = 55,6$.
Nếu đi trên cao tốc thì với $4,17$ lít xăng, xe chạy được $55,6$ km.
c) Bài toán được tóm tắt như sau:
| Loại đường | Chiều dài quãng (km) | Lượng xăng tiêu thụ (lít) |
| Đô thị | $100$ | $13,9$ |
| $20$ | $x$ | |
| Cao tốc | $100$ | $7,5$ |
| $80$ | $y$ | |
| Hỗn hợp | $100$ | $9,9$ |
| $30$ | $z$ |
Từ đó $x = (20,13,9) \, : \, 100 = 2,78$; $y = (80.7,5) \, : \, 100 = 6$; $z = (30.9,9) \, : \, 100 = 2,97$.
Do đó từ nhà về quê, xe ông An tiêu thụ hết $2,78 + 6 + 2,97 = 11,75$ lít xăng.
Câu 2. (1,5 điểm). Một bể chứa nước có dạng hình hộp chữ nhật được thiết kế với chiều dài, chiều rộng, chiều cao tỉ lệ với ba số $3$; $2$; $1$. Người ta mở một vòi cho nước vào bể. Gọi $x$ (dm) là chiều cao của bể. Hãy viết đa thức biểu thị số lít nước cần phải thêm vào bể để bể đầy nước, biết rằng trong bể đang có $100$ lít nước. Tính thời gian vòi chảy đầy bể trong trường hợp chiều cao bể là $5$ dm và mỗi phút vòi chảy được $25$ lít nước.
Hướng dẫn giải:
a) Chiều rộng, chiều dài, chiều cao của bể lần lượt là $3x; \, 2x; \, x$.
Bể có thể tích $3x.2x.x = 6x^3$
Bể chứa được $6x^3$
b) Trường hợp bể có chiều cao $5$ dm thì $x = 5$
Để đầy bể nước, cần mở vòi trong $650 \, : \, 25 = 26$
Câu 3. (1,0 điểm). Trong một cửa hàng bán các suất ăn nhanh, mỗi suất gồm một món chính và một món phụ với thực đơn như sau:
| Món chính | Món phụ |
| Cánh gà rán; đùi gà rán; phở | Khoai tây chiên; phô mai que |
Bạn Hải gọi ngẫu nhiên một suất đủ hai món. Tính xác suất xảy ra biến cố A: "Hải chọn suất ăn gồm đùi gà rán và phô mai que".
Hướng dẫn giải:
Xét $6$ biến cố sau:
A: "Hải chọn suất ăn gồm đùi gà rán và phô mai que".
B: "Hải chọn suất ăn gồm đùi gà rán và khoai tây chiên".
C: "Hải chọn suất ăn gồm cánh gà rán và phô mai que".
D: "Hải chọn suất ăn gồm cánh gà rán và khoai tây chiên".
E: "Hải chọn suất ăn gồm phở và phô mai que".
F: "Hải chọn suất ăn gồm phở và khoai tây chiên".
Ta thấy $6$ biến cố trên đồng khả năng và luôn xảy ra đúng một trong sáu biến cố này.
Vì vậy, mỗi biến cố trên đều có xác suất bằng $\dfrac16$. Nói riêng, biến cố $A$ có xác suất bằng $\dfrac16$.
Câu 4. (2,0 điểm). Cho tam giác $ABC$ có $AB<AC$. Trên cạnh $AC$ lấy điểm $D$ sao cho $AD = AB$. Gọi $M$ là trung điểm của $BD$; $E$ là giao điểm của tia phân giác góc $B$ với tia $AM$ tại $E$.
a) Chứng minh rằng tia $AM$ là tia phân giác góc $A$ của tam giác $ABC$.
b) Cho góc $C$ có số đo bằng $30^{\circ}$. Hãy tính số đo góc $ACE$.
Hướng dẫn giải:
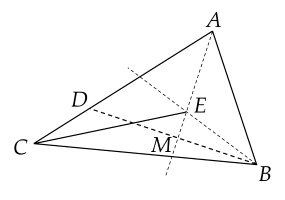
a) Xét $\triangle A D M$ và $\triangle A B M$ có
$A D=A B$ (già thiết);
$D M=B M$ (giả thiết $M$ là trung điểm của $B D$);
$A M$ chung.
Suy ra $\triangle A D M=\triangle A B M$ (c.c.c).
Do đó $\widehat{D A M}=\widehat{B A M}$ (hai góc tương ứng).
Vì vậy $A M$ là tia phân giác góc $A$ của tam giác $A B C$.
b) Theo chứng minh trên, có $A M$ là tia phân giác góc $A$.
Lại có $E$ là giao điểm của tia phân giác góc $B$ với tia $AE$ (giả thiết).
Như vậy $E$ là giao điểm của tia phân giác góc $A$ với tia phân giác góc $B$.
Suy ra $CE$ là phân giác góc $C$ (theo định lí: ba đường phân giác của tam giác đồng quy tại một điểm).
Từ đó $\widehat{A C E}=\dfrac{1}{2} \hat{C}=15^{\circ}$.
Câu 5. (0,5 điểm). Ông $A$ và ông $B$ đứng cách nhau $55$ mét. Một bộ phát wifi có bán kính hoạt động $35$ mét và cách ông $A$ $20$ mét. Em hãy cho biết điện thoại di động của ông $A$ hay ông $B$ không nhận được sóng wifi? Vì sao?
Hướng dẫn giải:
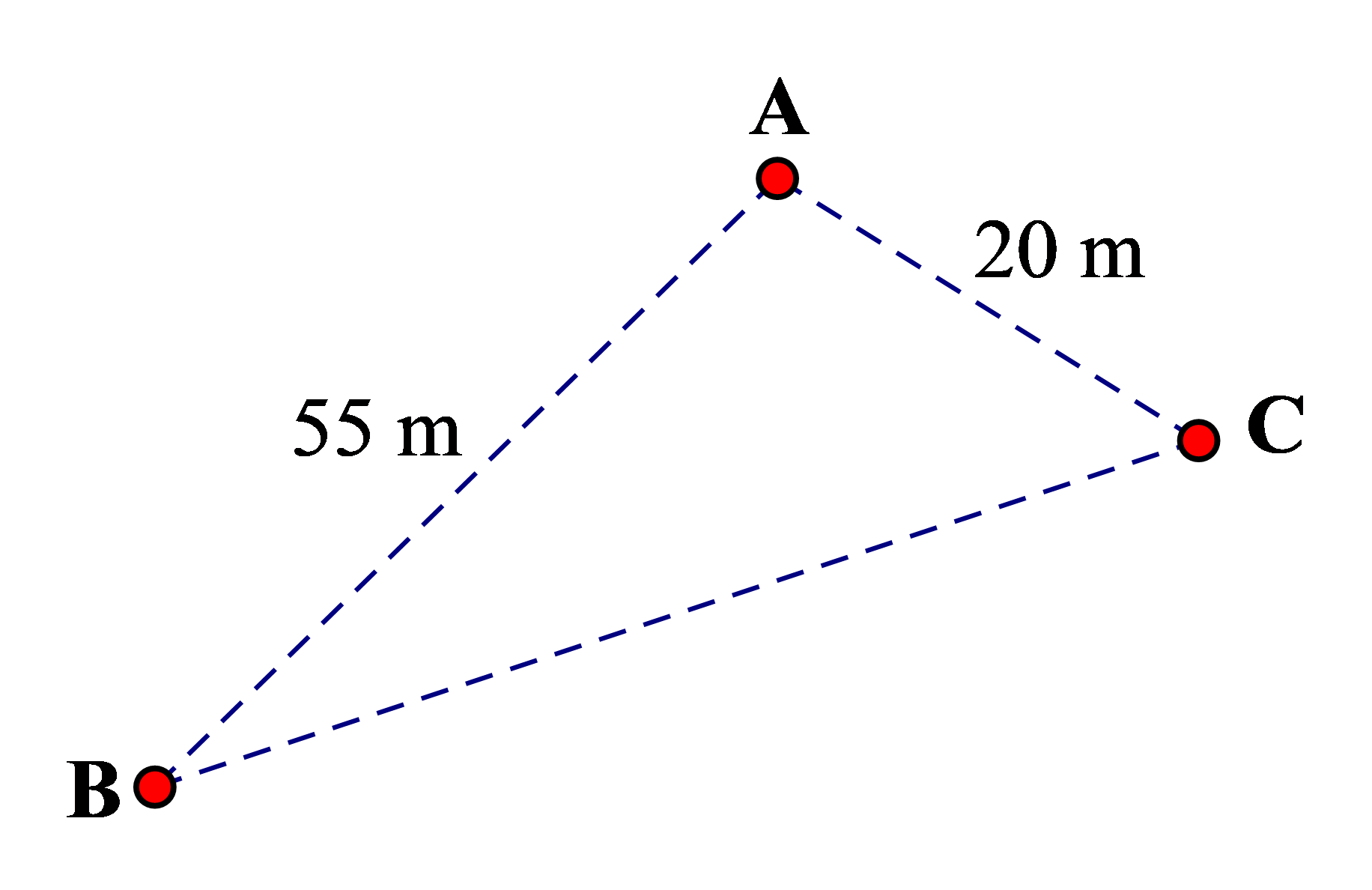
Kí hiệu $A, \, B$ là vị trí ông $A$ và ông $B$ đang đứng. $C$ là vị trí bộ phát wifi.
Trong $\triangle A B C$ có $B C>A B-A C=55-20=35$.
Suy ra khoảng cách từ ông $B$ đến vị trí bộ phát wifi lớn hơn bán kính hoạt động của bộ phát.
Do đó ông $B$ không nhận được sóng wifi.
Khoảng cách từ ông $A$ đến bộ phát wifi là $20$ m (nhỏ hơn bán kính hoạt động của bộ phát) nên ông $A$ nhận được sóng wifi.
