Đề kiểm tra giữa học kì II (đề số 1)

Câu 1 (1đ):

Khẳng định nào sau đây đúng?

\Big(\displaystyle \int f(x)\mathrm{d}x \Big)'=-F'(x)

.

\Big(\displaystyle \int f(x)\mathrm{d}x \Big)'=f(x)

.

\Big(\displaystyle \int f(x)\mathrm{d}x \Big)'=-f(x)

.

\Big(\displaystyle \int f(x)\mathrm{d}x \Big)'=F'(x)

.

Câu 2 (1đ):

Họ nguyên hàm của hàm số $f(x)=x^{2 \, 025}$ là

\displaystyle \int f(x) \mathrm{d}x=\dfrac{1}{2 \, 026}. x^{2 \, 026}+C

.

\displaystyle \int f(x) \mathrm{d}x=x^{2 \, 026}+C

.

\displaystyle \int f(x) \mathrm{d}x=\dfrac{1}{2 \, 024}.x^{2 \, 024}+C

.

\displaystyle \int f(x) \mathrm{d}x=2 \, 025.x^{2 \, 024}+C

.

Câu 3 (1đ):

Hàm số $F(x)=\ln x+x+1$ là một nguyên hàm của hàm số nào sau đây trên $(0;+\infty)$ ?

f(x)=x\ln x+x

.

f(x)=x\left(\ln x-1 \right)

.

f(x)=x\ln x+\dfrac{x^2}{2}+x

.

f(x)=\dfrac{1}{x}+1

.

Câu 4 (1đ):

Cho hàm số $f(x )$ liên tục trên $\mathbb{R}$ và $\displaystyle\int\limits_{0}^{8}{f(x )}\,\mathrm{d}x=10$ , $\displaystyle\int\limits_{5}^{8}{f(x )}\,\mathrm{d}x=4$ . Khi đó $\displaystyle\int\limits_{0}^{5}{f(x )}\,\mathrm{d}x$ bằng

6

.

4

.

7

.

3

.

Câu 5 (1đ):

Cho hai hàm số $f(x)$ và $g(x)$ liên tục trên $[ a;b]$ . Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y=f(x)$ , $y=g(x)$ và các đường thẳng $x=a$ , $x=b$ bằng

\displaystyle\int\limits_{a}^{b}{| f(x)-g(x) |\mathrm{d}x}

.

\displaystyle\int\limits_{a}^{b}{[ f(x)-g(x)]\mathrm{d}x}

.

\Big| \displaystyle\int\limits_{a}^{b}{[ f(x)-g(x)]\mathrm{d}x} \Big|

.

\displaystyle\int\limits_{a}^{b}{| f(x)+g(x)|\mathrm{d}x}

.

Câu 6 (1đ):

Trong không gian $Oxyz$ , cho đường thẳng $d:\dfrac{x-3}{4}=\dfrac{y+1}{-1}=\dfrac{z+2}{3}$ vuông góc với mặt phẳng $(P)$ . Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng $(P)$ ?

\overrightarrow{n}=(3\,;\,-1\,;\,2)

.

\overrightarrow{n}=(4\,;\,-1\,;\,3)

.

\overrightarrow{n}=(4\,;\,1\,;\,3)

.

\overrightarrow{n}=(3\,;\,1;\,\,2)

.

Câu 7 (1đ):

Trong không gian với hệ tọa độ $Oxyz,$ phương trình mặt phẳng $(\alpha)$ đi qua điểm $A(2;1;1)$ và vuông góc với trục tung là

z=1.

2x+y+z-4=0.

y=1.

x=2

.

Câu 8 (1đ):

Giá trị của tích phân $I = \displaystyle \int\limits_{-1}^1 \left| 2^x - 2^{-x} \right| \mathrm{d} x$ bằng

\dfrac{1}{\ln 2}

.

2\ln 2

.

\ln 2

.

\dfrac{2}{\ln 2}

.

Câu 9 (1đ):

Cho hàm số $y=f(x)$ có đạo hàm $f'(x )=\cos x+1,\forall x\in \mathbb{R}$ . Biết $\displaystyle\int\limits_{0}^{\frac{\pi }{2}}f(x )\mathrm{d}x=\dfrac{{{\pi }^{2}}}{8}+1$ , khi đó $f\Big(\dfrac{\pi }{2}\Big)$ bằng

\dfrac{\pi }{2}

.

1

.

\dfrac{\pi }{2}+1

.

\dfrac{\pi }{2}-1

.

Câu 10 (1đ):

Cho hình phẳng $\left(H \right)$ giới hạn bởi đồ thị hàm số $y=-\sqrt{x}$ , đường thẳng $y=-x+2$ và trục hoành.

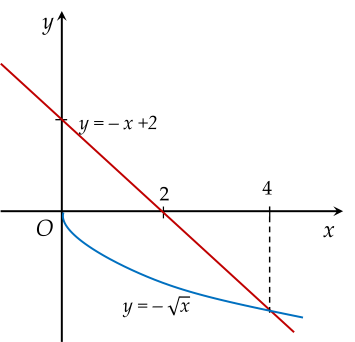
loading...

Khối tròn xoay tạo ra khi $\left(H \right)$ quay quanh $Ox$ có thể tích $V$ được xác định bằng công thức nào sau đây?

V= \int\limits_{0}^{2}{xdx+\int\limits_{2}^{4}{{{\left(x-2 \right)}^{2}}dx}}

.

V=\pi \Big[ \int\limits_{0}^{2}{xdx-\int\limits_{2}^{4}{{{\left(2-x \right)}^{2}}dx}} \Big]

.

V=\pi \Big[ \int\limits_{0}^{4}{xdx-\int\limits_{2}^{4}{{{\left(2-x \right)}^{2}}dx}} \Big]

.

V=\pi \Big[ \int\limits_{0}^{2}{xdx+\int\limits_{2}^{4}{{{\left(2-x \right)}^{2}}dx}} \Big]

.

Câu 11 (1đ):

Trong không gian $Oxyz,$ cho hai mặt phẳng $(P): \, x+3 z+2=0, \, (Q): \, x+3 z-4=0$ . Mặt phẳng song song và cách đều $(P)$ và $(Q)$ có phương trình là

x+3 z-1=0

.

x+3 z-2=0

.

x+3 z-6=0

.

x+3 z+6=0

.

Câu 12 (1đ):

$F(x)$ là một nguyên hàm của hàm số $f(x)=\mathrm{e}^{x}-1$ trên $(-\infty ;+\infty)$ / Biết $F(0)=2$ , hàm số $F(x)$ là

\dfrac{1}{\mathrm{e}^{x}}-x+1

.

\mathrm{e}^{x}-x+1

.

\ln x-x-1

.

\mathrm{e}^{x}-x-1

.

Câu 13 (1đ):

Cho hàm số $y=f(x)$ có đạo hàm là $f'(x)=6x+\sin x, \, \forall x\in \mathbb{R}$ . $F(x)$ là nguyên hàm của $f(x)$ thỏa mãn $F(0)=3$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $f(x) = 3x^2 - \cos x + C$ với $C \in \mathbb{R}$ .
b) Khi $f(0) = 0$ thì $f(x)=3x^2-\cos x-1$ .
c) Khi $f(0) = 0$ thì $F(x) = x^3 - \sin x$ .
d) Khi $f(0) = 0$ thì $F( \pi )=\pi^3+\pi +3$ .

Câu 14 (1đ):

Cho một viên gạch men có dạng hình vuông $OABC$ như hình vẽ. Sau khi tọa độ hóa, ta có $O(0;0 )$ , $A(0;1 )$ , $B(1;1 )$ , $C(1;0 )$ và hai đường cong lần lượt là đồ thị hàm số $y=x^3$ và $y=\sqrt[3]{x}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\sqrt[3]{x}$ , trục $Ox$ , đường thẳng $x=0$ và đường thẳng $x=1$ được tính bằng công thức $S=\displaystyle\int\limits_{0}^{1}{\|\sqrt[3]{x}\|}\,\mathrm{d}x$ .
b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=x^3$ , trục $Ox$ , đường thẳng $x=0$ và đường thẳng $x=1$ có giá trị bằng $\dfrac{3}{4}$ .
c) Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=x^3$ và $y=\sqrt[3]{x}$ , đường thẳng $x=0$ và đường thẳng $x=1$ được tính bằng công thức $S=\displaystyle\int\limits_{0}^{1}(x^3-\sqrt[3]{x})\mathrm{d}x$ .
d) Diện tích phần không được tô đậm trên viên gạch men có giá trị bằng $\dfrac{1}{2}$ .

Câu 15 (1đ):

Trong không gian $Oxyz$ , mặt phẳng $(P)$ đi qua hai điểm $M(2;0;-1)$ , $N(1;-1;3)$ và vuông góc với mặt phẳng $(Q):\,3x+2y-z+5=0$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{MN}=(-1;-1;4)$ .
b) Một vectơ pháp tuyến của mặt phẳng $(Q)$ là $\overrightarrow{n_Q}=(3;2-1).$
c) Vectơ pháp tuyến của mặt phẳng $(Q)$ cũng là vectơ pháp tuyến của mặt phẳng $(P)$ .
d) Phương trình mặt phẳng $(P): \, 7x-11y-9z+15=0$ .

Câu 16 (1đ):

Trong không gian với hệ tọa độ $Oxyz,$ cho các điểm $A(1;1;3 ),\,B(-1;3;2 ),\,C(-1;2;3 )$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Ba điểm $A,\,B,\,C$ không thẳng hàng.
b) $\overrightarrow{AB}=3\overrightarrow{KC}$ với $K(2;-2;2)$ .
c) Phương trình mặt phẳng $(ABC)$ là $x+2y+2z+9=0$ .
d) Khoảng cách từ $M(-4;4;0)$ đến $(ABC)$ lớn hơn khoảng cách từ $N(4;2;1)$ đến $(ABC)$ .

Câu 17 (1đ):

Một bác thợ xây bơm nước vào bể chứa nước. Gọi $h(t)$ là thể tích nước bơm được sau $t$ giây. Cho $h'(t)=3at^2+bt$ (m³/s) và ban đầu bể không có nước. Sau $5$ giây thì thể tích nước trong bể là $150$ m³. Sau $10$ giây thì thể tích nước trong bể là $1\,100$ m³. Thể tích nước trong bể sau khi bơm được $20$ giây là bao nhiêu m³? (Làm tròn kết quả đến chữ số hàng đơn vị)

Trả lời:

Câu 18 (1đ):

Hình dưới là đồ thị vận tốc $v(t)$ của một vật ( $t=0$ là thời điểm vật bắt đầu chuyển động).

loading...

Tính tổng quãng đường (m) vật di chuyển trong $5$ giây đầu tiên.

Trả lời:

Câu 19 (1đ):

Một khối cầu có bán kính là $5$ dm, người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng $3$ $dm$ để làm một chiếc lu đựng nước. Thể tích của chiếc lu bằng bao nhiêu? (làm tròn đến hàng đơn vị).

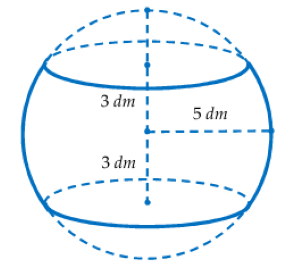
loading...

Trả lời: dm $^3$ .

Câu 20 (1đ):

Gọi $V$ là thể tích của khối tròn xoay giới hạn bởi đồ thị hàm số $y=x\sqrt{a}$ và $y=\sqrt{a\left(2-a \right)x},\ 0<a<2$ , khi quay quanh trục $Ox$ . Giá trị của $a$ để $V$ đạt giá trị lớn nhất là

Trả lời:

Câu 21 (1đ):

Trong không gian với hệ trục tọa độ $Oxyz$ . Phương trình mặt phẳng $(P)$ đi qua hai điểm $A(1;1;1),\,B(0;2;2)$ đồng thời cắt các tia $Ox,\,Oy$ lần lượt tại các điểm $M,\,N$ $(M, \, N$ không trùng với gốc tọa độ $O)$ thỏa mãn $OM=2ON$ là $ax+by+cz+d=0$ . Tính $T=a+b+c+d$ .

Trả lời:

Câu 22 (1đ):

Trong không gian $Oxyz$ , cho điểm $A(1\,011;1;0)$ và mặt phẳng $(Q): \, x-y-\sqrt{7}z+2=0$ . Biết $(P)$ // $(Q)$ và $(P)$ có dạng $x+by+cz+m=0$ . Tính $|T|$ , với $T$ tổng các giá trị của $m$ sao cho $d\big(A;(P)\big)=1$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì II (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì II (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP