Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
(1 điểm) Thực hiện các phép tính:
a) $0,75+\dfrac{9}{5}\left(1,5-\dfrac{2}{3}\right)^2$
b) $\dfrac{-22}{25}+\left(\dfrac{22}{7}-0,12\right)$
Hướng dẫn giải:
a) $\dfrac{3}{4}+\dfrac{9}{5}\left(\dfrac{3}{2}-\dfrac{2}{3}\right)^2=\dfrac{3}{4}+\dfrac{9}{5}\left(\dfrac{5}{6}\right)^2=\dfrac{3}{4}+\dfrac{9}{5} \cdot \dfrac{25}{36}=\dfrac{3}{4}+\dfrac{5}{4}=2$
b) $\dfrac{-22}{25}+\left(\dfrac{22}{7}-0,12\right) =\dfrac{-22}{25}+\left(\dfrac{22}{7}-\dfrac{12}{100}\right)=\dfrac{-88}{100}+\dfrac{22}{7}+\dfrac{-12}{100} =\left(\dfrac{-88}{100}+\dfrac{-12}{100}\right)+\dfrac{22}{7}=-1+\dfrac{22}{7}=\dfrac{15}{7}$
(0,5 điểm) Tìm $x$ thỏa mãn $(-0,25)^5: x=(-0,25)^3$.
Hướng dẫn giải:
Vì $(-0,25)^5: x=(-0,25)^3$ nên $x=(-0,25)^5:(-0,25)^3$
$x=(-0,25)^2=\left(-\dfrac{1}{4}\right)^2=\dfrac{1}{16}$
(0,75 điểm): Quãng đường từ sân vận động Old Trafford ở thành phố Manchester đến tháp đồng hồ Big Ben ở London (Vương quốc Anh) khoảng 200 dặm. Biết 1 dặm = 1,609344 km, hãy tính độ dài quãng đường đó theo đơn vị ki-lô-mét (làm tròn kết quả với độ chính xác 0,5 ).
Hướng dẫn giải:
Độ dài quãng đường từ sân vận động Old Trafford đến tháp đồng hồ Big Ben là $200 . 1,609344=321,8688$ km.
Để kết quả có độ chính xác $0,5$ ta cần làm tròn $321,8688$ đến chữ số hàng đơn vị, kết quả là $321,8688 \approx 322$ km.
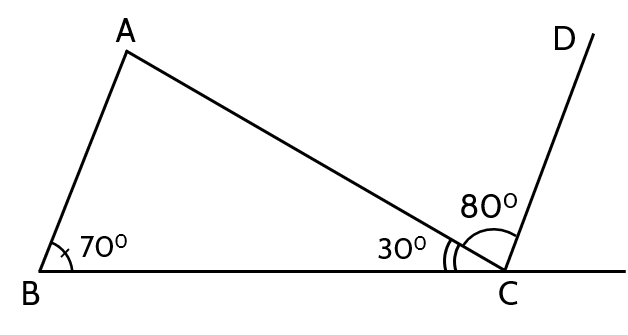
(0,75 điểm) Hãy chứng tỏ trong hình vẽ trên có$AB$ // $CD$.
Hướng dẫn giải:
Tính được $\widehat{B A C}=80^{\circ}$.
Lập luận: $\widehat{B A C}=\widehat{A C D}\left(=80^{\circ}\right)$ và hai góc ở vị trí so le trong, suy ra: $A B / / C D$.
(1,5 điểm) Cho $\triangle A B C$ cân tại $A$. Trên tia đối của tia $B C$ lấy điểm $D$, trên tia đối của tia $C B$ lấy điểm $E$ sao cho $B D=C E$.
a) Chứng minh: $\widehat{A B D}=\widehat{A C E}$.
b) Chứng minh: $\triangle A D E$ là tam giác cân.
Hướng dẫn giải:

a) $\triangle A B C$ cân tại $\mathrm{A} \Rightarrow \widehat{A B C}=\widehat{A C B}$ và $A B=A C$
Có $\widehat{A B D}+\widehat{A B C}=180^{\circ} ; \widehat{A C E}+\widehat{A C B}=180^{\circ}$
Mà $\widehat{A B C}=\widehat{A C B}$ nên suy ra $\widehat{A B D}=\widehat{A C E}$.
b)Chứng minh được $\triangle A B D=\triangle A C E(c . g . c)$
Suy ra $A D=A E$. Do đó $\triangle A D E$ cân tại $A$.
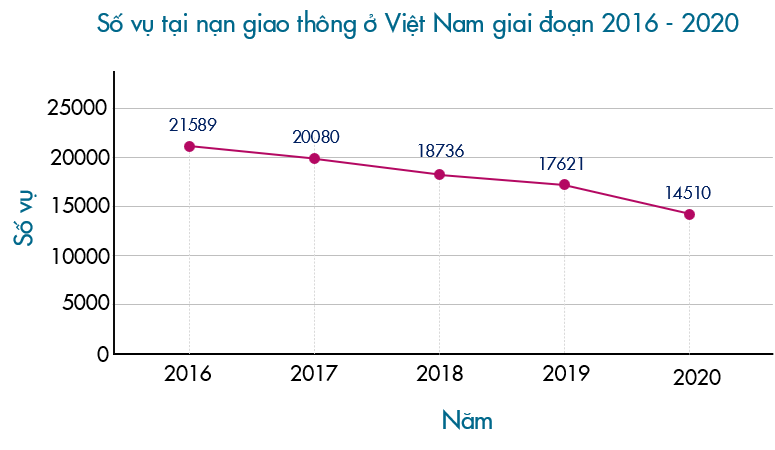
(1,5 điểm) Theo báo cáo của Ủy ban An toàn giao thông Quốc gia, số vụ tai nạn giao thông của nước ta trong giai đoạn từ 2016 – 2020 được thể hiện ở biểu đồ bên.
a) Dữ liệu về số vụ tai nạn giao thông của nước ta trong giai đoạn từ 2016 – 2020 được biểu diễn dưới dạng nào?
b) Dựa vào biểu đồ, hãy lập bảng số liệu thống kê số vụ tai nạn giao thông của nước ta.
c) Em có nhận xét gì về số vụ tai nạn giao thông của nước ta trong giai đoạn từ 2016 – 2020?
Hướng dẫn giải:
a) Biểu đồ đoạn thẳng
b) Bảng số liệu thống kê số vụ TNGT của nước ta giai đoạn 2016 – 2020
|
Năm |
2016 |
2017 |
2018 |
2019 |
2020 |
|
Số vụ |
21 589 |
20 080 |
18 736 |
17 621 |
14 510 |
c) Nhận xét: Số vụ TNGT của nước ta giai đoạn 2016 – 2020 liên tục giảm qua từng năm.

(1 điểm) “Để biết độ dài các cột đèn cao áp (trồng thẳng đứng) có bằng nhau không, ta có thể đo bóng của chúng dưới ánh sáng Mặt Trời mà không cần đo chính xác độ dài của mỗi cột”.
Do Mặt Trời ở xa Trái Đất nên có thể coi ánh sáng tạo với mặt đất những góc bằng nhau. Sử dụng hình vẽ bên, em hãy chứng tỏ nhận xét trên.
Hướng dẫn giải:

Giả sử bóng của hai cột đèn bằng nhau, tức là BC = EF.
Suy ra ΔABC = ΔDEF (g.c.g)
⇒ AB = DE (cạnh tương ứng của hai tam giác bằng nhau)
Do đó chiều cao hai cột đèn cao áp là bằng nhau.
